ПОСТРОЕНИЕ МОДЕЛЕЙ ГИДРОДИНАМИЧЕСКИХ И ТЕПЛОВЫХ ПРОЦЕССОВ

УРАВНЕНИЕ ГИДРАВЛИЧЕСКОЙ ЕМКОСТИ

Пусть элементом системы будет гидравлическая емкость резервуар с жидкостью (рис.1,а), в котором должен поддерживаться постоянным уровень жидкости.

а)   б)

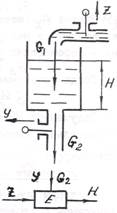
Рис.1

Регулируемая величина - выходная переменная элемента - высота уровня жидкости Н, изменяющаяся благодаря изменению расходов G₁ и G₂ ,

Расходы жидкости G₁ и G₂ (м³/с) зависят от перемещений z и y соответствующих клапанов; кроме того, расход G₂ зависит от напора. Таким образом,

G₁ = G₁ (z)

и

G₂ = G₂ (у, Н)

Перемещения клапанов z и y являются входными величинами элемента.

Блок-схема емкости изображена на рис.1, б.

В установившемся режиме G₁ = G₂ и высота уровня жидкости остается неизменной (Н = const). При изменении какого-либо из расходов или одновременном изменении их высота уровня изменяется.

Составим уравнение материального баланса емкости.

За малый промежуток времени dt количество жидкости в резервуаре измениться на. dG м³ , так как в емкость поступит G₁dt м³ жидкости, а сольется G₂dt м³, то есть

dG = (G₁ - G₂) dt

Но изменение количества жидкости в резервуаре можно представить как произведение площади поперечного сечения резервуара и изменения высоты уровня

dG = S dH

поэтому можно записать

S dH = (G₁ - G₂) dt или .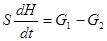

Подставив вместо G₁ и G₂ их выражения, получим уравнение емкости

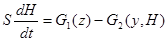
Предположим, что клапан подачи жидкости имеет такой профиль, что расход G₁, пропорционален z:

G₁ = аz.

Расход G₂ через сливной клапан пропорционален корню квадратному из напора Н и при соответствующем профиле клапана - перемещению у:

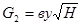
Тогда уравнение емкости запишется в виде

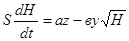
Полученное уравнение является нелинейным уравнением, следовательно, емкость представляет собой нелинейный элемент.

ОПИСАНИЕ ТЕПЛОПЕРЕНОСА

Рассмотрим вопрос математического описания теплопереноса с учетом аналогии и взаимосвязи этого процесса с массопереносом Имеем поле температур

T = f (х, у, z, t),

где х, у, z — координаты точки в пространстве;

t — время.

Рассмотрим в трехмерном пространстве две изотермические поверхности, все точки которых имеют температуры Т и Т+ΔТ соответственно. Изменение температур в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности, причем наиболее резкое изменение температуры происходит в направлении нормали n к изотермической поверхности. Вектор, длина которого равна пределу отношения изменения температуры ΔТ к расстоянию Δn между изотермическими поверхностями по нормали, а направление совпадает с направлением нормали, называется температурным градиентом:

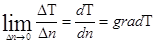
т. е. grad T — вектор, направленный по нормали к поверхности уровня и численно равный скорости изменения Т по этому направлению. Для скалярного поля Т (х, у, z) этот вектор вычисляется по следующей формуле

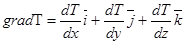
где 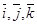— единичные векторы, направленные по координатным осям х, у, z.

Передача тепла в неподвижной среде описывается законом Фурье

q_T = — λ grad T ,

где q_T — тепловой поток (количество вещества, передаваемое через единицу поверхности в единицу времени);

λ — коэффициент теплопроводности.

В чистом виде такой процесс можно наблюдать лишь в твердых телах. В газах и жидкостях на этот процесс оказывает влияние движения среды, т. е. свободная и вынужденная конвекция. С учетом конвекции закон Фурье можно представить в следующем виде:

q_T = — λ grad T + с_р ρ w T,

где с_р — теплоемкость при постоянном давлении;

ρ — плотность среды;

w — скорость потока.

Это уравнение целесообразно использовать при ламинарном (Re<2300) и переходном (2300 < Re < 10000) режиме движения потока.

Выше были рассмотрены процессы передачи тепла внутри среды с определенными физическими свойствами. Остановимся на вопросе теплообмена между средами.

Для этой цели часто пользуются эмпирическим законом теплопереноса

q_T = α ΔT

где ΔT — разность температур;

α — коэффициент теплоотдачи.

Теплообмен между двумя поверхностями, нагретыми до температур Т₁ и Т₂ при преобладании теплопередачи излучением в соответствие с законом Стефана — Больцмана описывается уравнением

q_И = ε С₀(Т₁⁴ – Т₂⁴),

где ε — приведенная степень черноты;

С₀ — коэффициент лучеиспускания абсолютно черного тела.

Чаще всего передача тепла теплопроводностью, конвекцией и излучением наблюдается одновременно. В этом случае пользуются общим коэффициентом теплоотдачи, представляя тепловой поток в виде

q₀ = α₀(Т₁ – Т₂) = (α_с + α_л) (Т₁ – Т₂)

где α₀ — общий коэффициент теплоотдачи;

α_с и α_л — коэффициенты теплоотдачи соприкосновением и лучеиспусканием.

В ряде случаев, особенно при большой доли теплопередачи излучением, лучшие результаты может дать уравнение по структуре аналогичное

q_И = ε С₀(Т₁⁴ – Т₂⁴), т.е. q₀ = (ε_с + ε) С₀(Т₁⁴ – Т₂⁴).

Влияние конвективного теплообмена учитывается здесь увеличением степени черноты на некоторую величину ε_с.

Следует заметить, что лишь в некоторых относительно простых случаях можно пользоваться табличными значениями указанных коэффициентов. В большинстве же реальных металлургических агрегатов эти коэффициенты приходится определять экспериментально-статистическими методами. Однако роль теоретических представлений и здесь остается решающей, так как они позволяют определить адекватную структуру математической модели.