МОДЕЛЬ СТРУКТУРЫ ПОТОКОВ ДЛЯ ШБМ

Для получения обобщенного описания процесса измельчения в ШБМ используется модель структуры потоков, схема которой приведена на рис. 1. Модель представляет комбинацию последовательно расположенных зон смешения и вытеснения с участками структурных неоднородностей потока: байпасом, рециклом и застойными зонами. Появление застойных областей в объеме зоны измельчения ШБМ объясняется дросселирующей способностью межкамерной и выходных перегородок, различной плотностью "упаковки" мелющих тел, явлением агрегирования, наличием критического размера зерен измельчаемого материала. Внутренний рецикл обусловлен наличием обратного потока - переносом части материала в направлении, обратном направлению движения основного потока. Явление байпаса обусловлено наличием в потоке материала частиц, время пребывания которых в зоне измельчения меньше среднего времени измельчения.

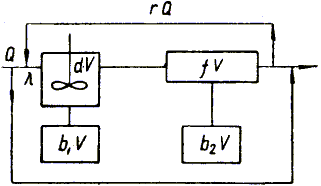
Рис. 1. Представление структуры потока материала в ШБМ

в виде комбинированной модели

Система уравнений для данной модели представляется в следующем виде:

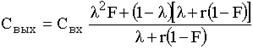, (1)

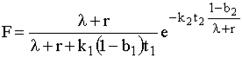, (2)

где C_вых - содержание недомолотого продукта на выходе из ШБМ, С_вх - содержание недомолотого продукта на входе в ШБМ, - доля потока, проходящего через последовательно расположенные зоны смешения и вытеснения (при доле байпасирующего потока 1- (рис. 1), b₁ (b₂) - доля объема зоны измельчения, занимаемая застойной зоной, присоединенной к зоне смешения (вытеснения), r - доля потока, занимаемая внутренним рециклом, d и f - доли объема зоны измельчения, занимаемые идеальным смешение и вытеснением (d+f=1, рис. 1). При задании различных значений параметров d, f, , b₁, b₂, r можно получать различные типы моделей, отражающие характер процессов в ШБМ.

В обобщенном виде уравнение кинетики модели измельчения в ШБМ можно представить в виде:

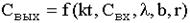(3)

Гидродинамическое уравнение потока материала в ШБМ имеет вид (диффузионное уравнение):

,

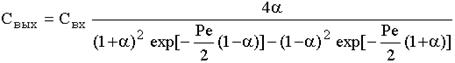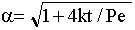, (4)

где Pe - число Пекле - главная гидродинамическая характеристика потока материала в ШБМ, определяющая основные геометрические характеристики.

Совместное решение (3) и (4) позволяет вычислить число Пекле. Для этого из уравнения (3) определяется величина kt (соответствующая модели). При подстановке kt в (4) выражение для числа Пекле будет иметь вид:

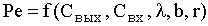(5)

Числам Пекле соответствуют оптимальные отношения L/D между длиной (L) и диаметром (D) ШБМ, определенные для цементных мельниц [1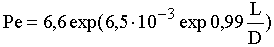6]:

(6)

Таким образом, алгоритм расчета математической модели процесса измельчения в ШБМ на основе структуры гидродинамики потоков можно представить виде, представленном на рис. 2.

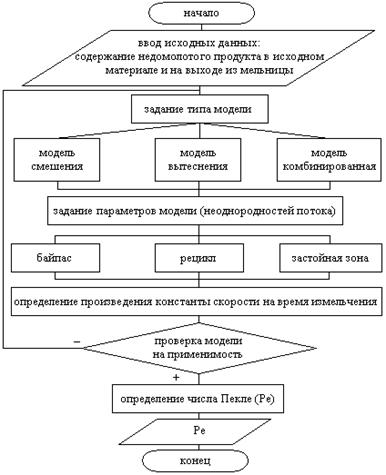
Рис. 2. Алгоритм расчета математической модели процесса измельчения в ШБМ на основе структуры гидродинамики потоков

Проверка установленного типа и параметров модели производится по найденному из системы (3) значению kt, оно должно входить в пределы, определяемые конструктивными и технологическими параметрами существующих ШБМ.