МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИЗМЕЛЬЧЕНИЯ

Построение математического описания процесса измельчения возможно двумя путями. Первый путь: когда математическое описание процесса в масштабе всего аппарата строится на основе математического описания в локальном объеме. Второй подход основан на составлении математического описания процесса измельчения с учетом закономерностей, имеющих место не в локальном объеме аппарата, а во всем рабочем пространстве, но без учета внутренней структуры и механизма измельчения.

Первый подход к моделированию процесса измельчения заключается в составлении обобщенного математического описания процесса измельчения и смешения на основе методов механики гетерогенных сред, получении в явном виде выражений для движущих сил измельчения частиц дисперсных фаз в многофазном потоке и на этой основе вскрытии механизма разрушения частиц [12]. Это позволяет в явном виде получить научно-обоснованные выражения вероятности разрушения частиц. На основе обобщенного математического описания строятся математические модели процессов измельчения в аппаратах различного принципа действия. Сложность данного подхода заключается в большом количестве идентификационных параметров и как следствие возникает необходимость в каждом конкретном случае прибегать к специальным экспериментальным исследованиям.

Второй подход к моделированию процесса измельчения представлен широким спектром методик. Так в статистических моделях [6] процесс представляется в виде выраженной полиномом зависимости целевой функции от ряда факторов, для определения коэффициентов полинома проводятся серии опытов. Другая методика в рамках рассматриваемого подхода заключается в использовании математического аппарата случайных марковских процессов "рождения" и "агломерации" частиц измельчаемого продукта [1]. При использовании данной методики получаются достаточно простые зависимости, параметры которых характеризуют конкретный аппарат для измельчения. Внимания заслуживают матричные модели [15], в которых предполагается, что частицы всех классов крупности разрушаются с определенной вероятностью, продукты разрушения при этом могут попадать либо в исходный, либо в любой меньший класс крупности. Для этого класса моделей составляются уравнения, содержащие матричное представление функций исходного грансостава, разрушения, отбора и классификации для каждого класса крупности материала.

В рамках второго подхода к моделированию процесса измельчения был предложен ряд типовых моделей структуры потока материала (вещества) в аппаратах для измельчения [4, 5, 7, 8, 9, 10, 11, 16]: модель идеального вытеснения, модель идеального смешения, ячеечная и диффузионная модели (табл. 1).

Таблица 1

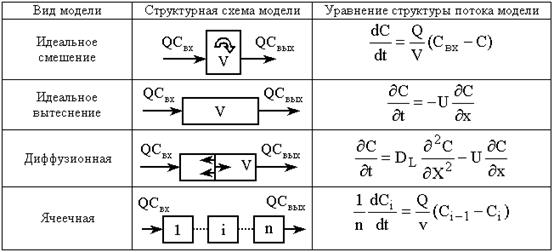
Модели, представленные в виде дифференциальных уравнений (табл. 1), выражают зависимость между C - главной характеристикой продукта (остатком на контрольном сите/долей недомолотого материала) и параметрами процесса (Q - весовым расходом, V - весовой загрузкой, U - линейной скоростью движения материала, D_L - коэффициентом обратного перемешивания, n - числом ячеек, x - линейной координатой, L - длиной аппарата), включая также и время измельчения (t).

Один из основных показателей, в соответствии с которым осуществляется выбор и проектирование технологических аппаратов для процессов, связанных с какими-либо превращениями вещества (например, для измельчения), является время, необходимое для того, чтобы превращение (измельчение) вещества происходило с достаточной полнотой. Зависимости характеристики готового продукта от временного фактора, а именно от произведения константы скорости реакции (измельчения) на время измельчения, дают решения дифференциальных уравнений моделей (табл. 1). Для типовых моделей, без учета факторов неоднородностей потока, решения дифференциальных уравнений представлены в табл. 2.

Таблица 2

Результирующие уравнения (табл. 2) позволяют по исходной характеристике измельчаемого материла С_вх определить характеристику продукта на выходе из аппарата С_вых после измельчения.

Модели процесса измельчения на основе описания в локальном объеме отличаются полнотой описания процесса измельчения в конкретном типе аппарата. Сложность данного подхода заключается в большом количестве идентификационных параметров и как следствие возникает необходимость в каждом конкретном случае прибегать к специальным экспериментальным исследованиям. Этот недостаток препятствует использовать методику описания процесса измельчения на основе локального объема в автоматизированном проектировании.

Более широкое применение получили модели без учета внутренней структуры и механизма процесса измельчения. Среди упомянутых выше моделей следует выделить математические модели гидродинамической структуры потоков. Введение понятия модели потока, т.е. использование приближенных представлений о внутренней структуре потока, позволяет получать математические описания процессов, относительно простые по своей структуре и удовлетворяющие точности, необходимой в инженерных расчетах. Кроме того, уравнения структуры потоков позволяют получать теоретические зависимости для основных конструктивных размеров аппаратов для измельчения (для ШБМ отношение длины к диаметру барабана). Этим обусловлена целесообразность выбора математических моделей на основе гидродинамики структуры потоков для создания САПР ШБМ.