Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал 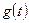 ;
;
б) система, описываемая дифференциальным уравнением
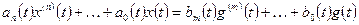 ;
;
в) начальные условия:
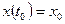 ,
, 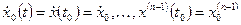 .
.
Требуется найти выходной сигнал 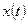 .
.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти свободное движение, решив однородное дифференциальное уравнение (1.26) с заданными начальными условиями (1.24).
2. Найти вынужденное движение, решив неоднородное дифференциальное уравнение (1.23) с нулевыми начальными условиями.
3. Определить выходной сигнал как сумму свободного и вынужденного движений.
Пример 1.9. Найти реакцию системы, описываемой дифференциальным уравнением
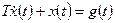 ,
, 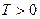 ,
,
на входной сигнал 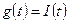 при нулевых начальных условиях.
при нулевых начальных условиях.
1. Найдем свободное движение. Так как начальные условия нулевые, свободное движение отсутствует, т.е. 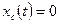 .
.
2. Найдем вынужденное движение как решение уравнения 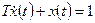 при условии
при условии 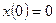 :
:
а) общее решение однородного уравнения
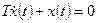 .
.
Характеристическое уравнение 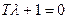 имеет корень
имеет корень 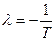 . Согласно (1.30)
. Согласно (1.30)
общее решение однородного уравнения имеет вид 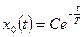 ;
;
б) частное решение неоднородного уравнения 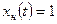 ;
;
в) общее решение неоднородного уравнения:
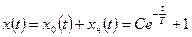 ;
;
г) из начального условия 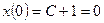 следует
следует 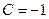 . Окончательно
. Окончательно
получаем 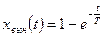 .
.
3. Выходной сигнал определяется вынужденным движением
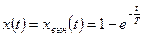 ,
, 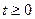 .
.
Реакция апериодического звена на единичное ступенчатое воздействие изображена на рис. 1.6, в.
Пример 1.10. Найти реакцию колебательного звена, описываемого дифференциальным уравнением
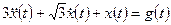 ,
,
на входное воздействие 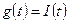 при нулевых начальных условиях (здесь
при нулевых начальных условиях (здесь 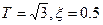 ).
).
1. Найдем свободное движение. Так как начальные условия нулевые, свободное движение отсутствует, т.е. 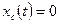 .
.
2. Найдем вынужденное движение, которое является решением неоднородного дифференциального уравнения 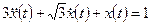 при нулевых начальных условиях
при нулевых начальных условиях 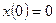 ,
, 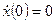 :
:
а) общее решение однородного уравнения:
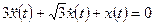 .
.
Характеристическое уравнение 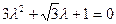 имеет корни
имеет корни
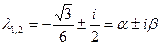
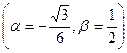 .
.
Согласно (1.32) общее решение однородного уравнения имеет вид
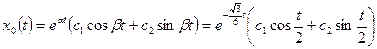 ;
;
б) частное решение неоднородного уравнения: 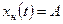 . В результате подстановки в неоднородное уравнение имеем
. В результате подстановки в неоднородное уравнение имеем 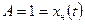 ;
;
в) общее решение неоднородного уравнения:
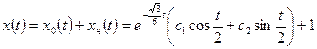 ;
;
г) из начальных условий
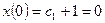 ,
,
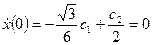
получаем 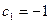 ,
, 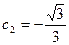 , а вынужденное движение
, а вынужденное движение
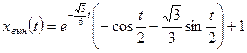 .
.
3. Выходной сигнал определяется вынужденным движением:
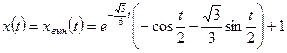 .
.
Пример 1.11. Найти свободное и вынужденное движения, а также выходной сигнал системы, описываемой дифференциальным уравнением
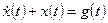 ,
,
с начальным условием 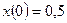 при входном сигнале
при входном сигнале 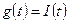 .
.
1. Определяем свободное движение как решение однородного дифференциального уравнения 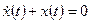 при начальном условии
при начальном условии 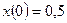 .
.
Характеристическое уравнение 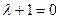 имеет корень
имеет корень 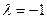 . Согласно (1.30) общее решение однородного уравнения имеет вид
. Согласно (1.30) общее решение однородного уравнения имеет вид 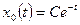 . Из начального условия получаем
. Из начального условия получаем 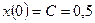 , и окончательно свободное движение
, и окончательно свободное движение
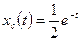 .
.
2. Находим вынужденное движение как решение неоднородного дифференциального уравнения 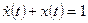 при начальном условии
при начальном условии 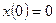 :
:
а) общее решение однородного уравнения имеет вид 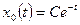 (см. п.1);
(см. п.1);
б) частное решение неоднородного уравнения ищется в виде 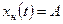 . В результате подстановки в неоднородное уравнение имеем
. В результате подстановки в неоднородное уравнение имеем 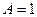 ,
, 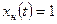 ;
;
в) общее решение неоднородного уравнения:
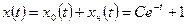 ;
;
г) из начального условия 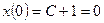 следует
следует 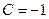 . Тогда вынужденное движение
. Тогда вынужденное движение
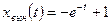 .
.
3. Выходной сигнал определяется по формуле (1.25):
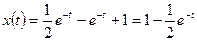 ,
, 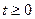 .
.
Пример 1.12. Найти свободное и вынужденное движения, а также выходной сигнал системы, описываемой дифференциальным уравнением
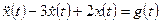 ,
,
с начальными условиями 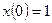 ,
, 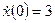 при входном сигнале
при входном сигнале
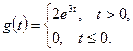
1. Определяем свободное движение как решение однородного дифференциального уравнения 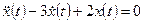 при начальных условиях
при начальных условиях 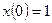 ,
, 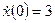 .
.
Характеристическое уравнение 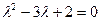 имеет два корня:
имеет два корня: 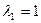 ,
, 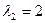 .
.
Согласно (1.30) получаем общее решение однородного уравнения:
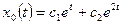 .
.
Из начальных условий
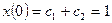 ,
,
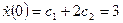 .
.
имеем 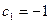 ,
, 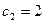 , а свободное движение
, а свободное движение
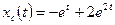 .
.
2. Находим вынужденное движение как решение неоднородного дифференциального уравнения 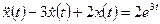 при условиях
при условиях 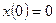 ,
, 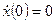 :
:
а) общее решение однородного уравнения получено в п.1:
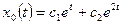 ;
;
б) частное решение неоднородного уравнения 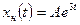 . Подставляя в неоднородное уравнение, имеем:
. Подставляя в неоднородное уравнение, имеем: 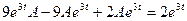 . Отсюда
. Отсюда 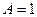 ,
, 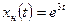 ;
;
в) общее решение неоднородного уравнения:
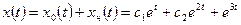 ;
;
г) подставляя в начальные условия, получаем:
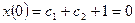 ,
,
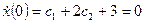 .
.
Отсюда 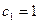 ,
, 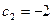 , а вынужденное движение
, а вынужденное движение
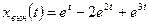 .
.
3. Выходной сигнал определяется по формуле (1.25):
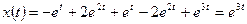 ,
, 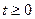 .
.
Пример 1.13. Найти свободное и вынужденное движения, а также выходной сигнал системы, описываемой уравнением
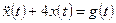
с начальными условиями 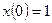 ,
, 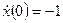 при входном сигнале
при входном сигнале
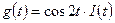 .
.
□ 1. Определяем свободное движение как решение однородного дифференциального уравнения 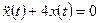 при начальных условиях
при начальных условиях 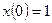 ,
, 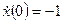 .
.
Характеристическое уравнение 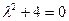 имеет два комплексных сопряженных корня
имеет два комплексных сопряженных корня 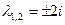 (
( 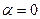 ,
, 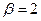 ). Согласно (1.32) получаем общее решение однородного уравнения:
). Согласно (1.32) получаем общее решение однородного уравнения:
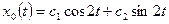 .
.
Из начальных условий
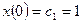 ,
,
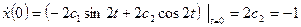
имеем 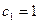 ,
, 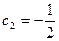 , а свободное движение
, а свободное движение
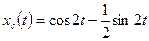 .
.
Дата добавления: 2017-09-01; просмотров: 2584;











