Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал 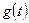 (см. разд. 1.2.1);
(см. разд. 1.2.1);
б) система, описываемая уравнениями состояния и выхода
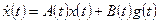 ,
, 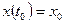 ,
,
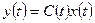 ;
;
в) вектор начальных состояний 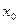 (см. разд. 1.2.1).
(см. разд. 1.2.1).
Требуется найти законы изменения вектора состояния 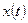 и вектора выхода
и вектора выхода 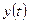 .
.
З а м е ч а н и е. Если система образована соединениями подсистем, то она заменяется эквивалентной системой так, как показано в разд. 1.2.2.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти переходную матрицу (одним из трех способов, рассмотренных далее).
2. Используя соотношения (1.44), (1.45) или (1.51), (1.52) в зависимости от типа системы, определить законы изменения векторов состояния и выхода.
Рассмотрим различные способы нахождения переходной матрицы.
Первый способ. Если фундоменальная матрица 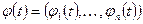 , столбцы которой образуют фундаментальную систему решений однородной системы дифференциальных ураннений (1.43), известна, то переходная матрица находится по формуле
, столбцы которой образуют фундаментальную систему решений однородной системы дифференциальных ураннений (1.43), известна, то переходная матрица находится по формуле
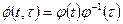 , (1.53)
, (1.53)
З а м е ч а н и е. Общее решение однородной системы (1.43) можно записать в виде
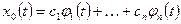 , (1.54)
, (1.54)
где 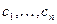 — произвольные постоянные
— произвольные постоянные
Для стационарных систем следует выполнить действия:
1. Найти корни характеристического уравнения
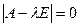 , (1.55)
, (1.55)
где 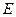 — единичная матрица.
— единичная матрица.
2. Выписать выражение общего решения (1.54) для каждой компоненты вектора х, следуя известным правилам в зависимости от типа корней (см. разд. 1.1.4). При этом произвольные постоянные в выражениях различны.
3. Полученные выражения подставить в однородную систему. Во многих случаях достаточно подставить в первые 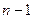 уравнений системы, что облегчает решение задачи.
уравнений системы, что облегчает решение задачи.
4. Приравнять коэффициенты при одинаковых функциях аргумента t и решить полученную систему уравнений.
5. Выписать общее решение, зависящее от n произвольных постоянных в форме (1.54). В результате находится фундаментальная матрица, а по формуле (1.53) — переходная.
Пример 1.21. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
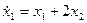 ,
,
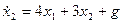 .
.
□ Составим матрицу системы 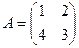 . Используем приведенный выше
. Используем приведенный выше
алгоритм.
1. Корни характеристического уравнения 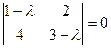 ,
, 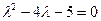 действительные разные:
действительные разные: 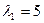 ,
, 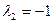 .
.
2. Запишем выражения общего решения для каждой компоненты:
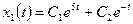 ,
,
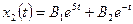 .
.
3. Подставим полученные соотношения в первое уравнение системы:
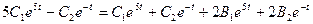 .
.
4. Приравняв коэффициенты при 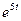 и
и 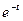 , получим
, получим
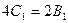 , или
, или 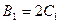 ,
,
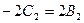 ,
, 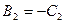 .
.
5. Из пп. 2, 4 имеем
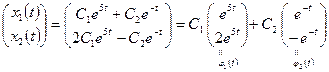 .
.
Отсюда
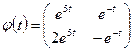 ,
, 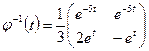
и по формуле (1.53)
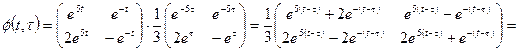
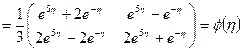 .
.
Пример 1.22. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
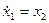 ,
,
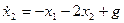 .
.
□ Составим матрицу системы 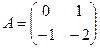 . Используем приведенный выше алгоритм.
. Используем приведенный выше алгоритм.
1. Корень характеристического уравнения 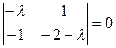 ,
, 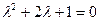 действительный кратный:
действительный кратный: 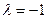 ,
, 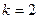 .
.
2. Выражения общего решения для каждой компоненты имеют вид
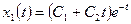 ,
,
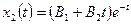 .
.
3. Подставим полученные соотношения в первое уравнение системы:
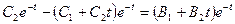 .
.
4. Приравняв коэффициенты при 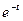 и
и 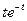 , получим
, получим
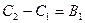 ,
,
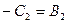 .
.
5. Из пп. 2, 4 имеем
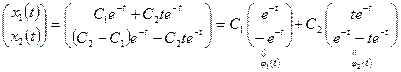 .
.
Отсюда находится фундаментальная матрица
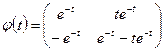 ,
, 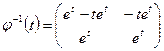
и по формуле (1.53)
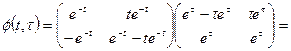
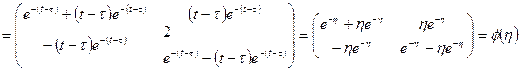 .
.
В случае нестационарных систем для определения фундаментальной матрицы можно воспользоваться следующим приемом, позволяющим уменьшить порядок системы, если известно ее решение  и
и  при
при 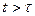 .
.
Тогда вектор-функции 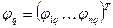 ,
, 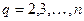 , образующие вместе с функцией
, образующие вместе с функцией 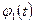 фундаментальную систему решений для (1.43), можно найти по формулам
фундаментальную систему решений для (1.43), можно найти по формулам
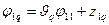 ,
,
…
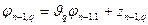 ,
, 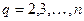 , (1.56)
, (1.56)
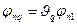 ,
,
где
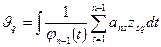 ,
,
а функции 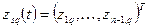 ,
, 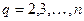 являются линейно независимыми решениями системы
являются линейно независимыми решениями системы 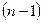 порядка
порядка
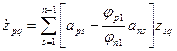 ,
, 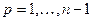 . (1.57)
. (1.57)
Пример 1.23. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
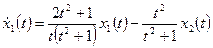 ,
,
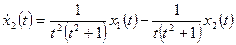 .
.
□ Для определения переходной матрицы 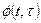 нужно найти два линейно независимых решения заданной системы. Первое решение будем искать с помощью рядов, представляя функции
нужно найти два линейно независимых решения заданной системы. Первое решение будем искать с помощью рядов, представляя функции 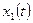 ,
, 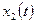 в виде
в виде
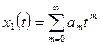 ,
, 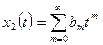 .
.
Подставив эти функции в систему, предварительно умножив первое уравнение на 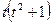 , а второе — на
, а второе — на 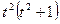 , имеем
, имеем
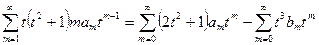 ,
,
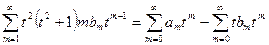 .
.
Приравнивая коэффициенты при одинаковых степенях 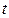 , получаем
, получаем
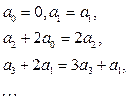
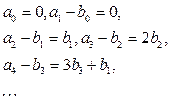
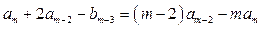 ,
, 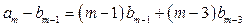 ,
,
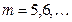 .
.
Данной системе уравнений удовлетворяют коэффициенты:
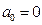 ,
, 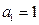 ,
, 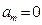 ,
, 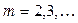 ;
;
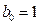 ,
, 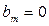 ,
, 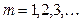 .
.
Таким образом, вектор-функция 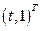 является решением системы.
является решением системы.
Обозначим это решение 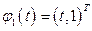 . Так как
. Так как 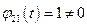 при всех
при всех 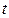 , можно понизить порядок системы. Согласно (1.56) второе решение
, можно понизить порядок системы. Согласно (1.56) второе решение 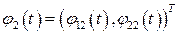 ищется в виде
ищется в виде
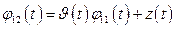 ,
, 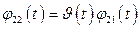 ,
,
где 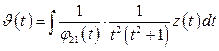 , а
, а 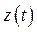 - решение системы (1.57), которая в данном случае состоит из одного уравнения
- решение системы (1.57), которая в данном случае состоит из одного уравнения 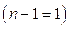 :
:
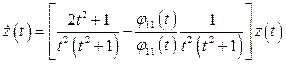 .
.
Подставляя 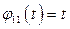 и
и 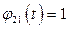 , получаем уравнение
, получаем уравнение
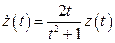 ,
,
решение которого находится с помощью разделения переменных, т.е. 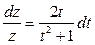 . В результате
. В результате 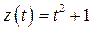 . Тогда
. Тогда 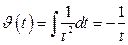 и, следовательно,
и, следовательно, 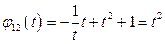 ,
, 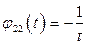 .
.
По найденным решениям 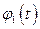 и
и 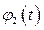 составляем фундаментальную матрицу
составляем фундаментальную матрицу
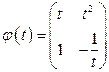 и
и 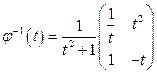 .
.
По формуле (1.53) имеем
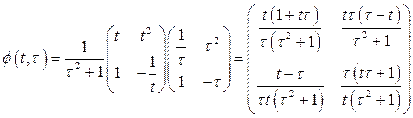
Второй способ. Применение теоремы разложения Сильвестра [60]. Переходная матрица стационарной системы определяется по формуле
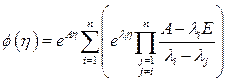 , (1.58)
, (1.58)
Где 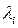 - собственные значения матрицы
- собственные значения матрицы 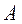 (здесь предполагается, что они различны), a
(здесь предполагается, что они различны), a 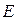 - единичная матрица.
- единичная матрица.
Пример 1.24. Найти законы изменения векторов состояния и выхода многомерной системы:
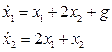 ,
, 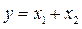
с начальными условиями 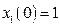 ,
, 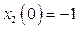 , при входном сигнале
, при входном сигнале
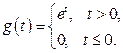
1. Перепишем уравнения системы в матричной форме:
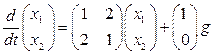 ,
, 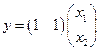 .
.
2. Найдем переходную матрицу. Для этого определим собственные значения матрицы 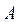 . Получим
. Получим
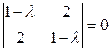 ,
, 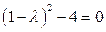 .
.
Отсюда 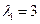 ,
, 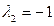 . По формуле (1.58) имеем
. По формуле (1.58) имеем
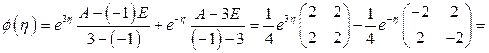
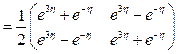 .
.
3. По формулам (1.51), (1.52) найдем законы изменения векторов состояния и выхода:
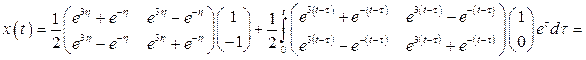
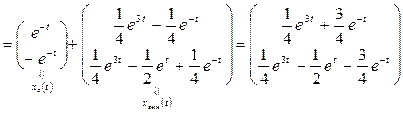 ,
,
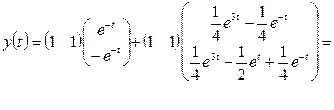
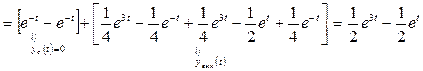 .
.
Пример 1.25. Найти законы изменения векторов состояния и выхода многомерной системы:
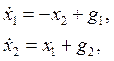
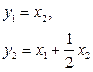
с начальными условиями 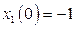 ,
, 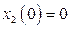 при входном сигнале
при входном сигнале
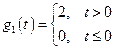 ,
, 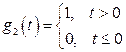 .
.
1. Перепишем уравнения системы в матричной форме:
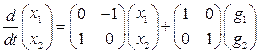 ,
, 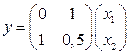 .
.
2. Найдем переходную матрицу. Для этого определим собственные значения матрицы 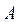 . Получим
. Получим
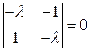 ,
, 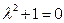 .
.
Отсюда 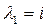 ,
, 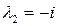 . По формуле (1.58) имеем
. По формуле (1.58) имеем
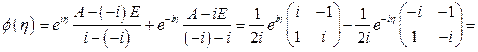
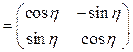 ,
,
так как 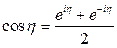 ,
, 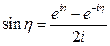 .
.
3. Mo формулам (1.51), (1.52) найдем законы изменения векторов состояния и выхода:
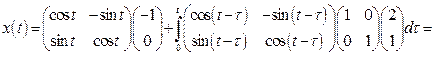
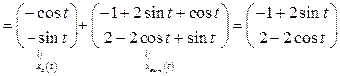 ,
,
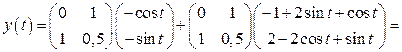
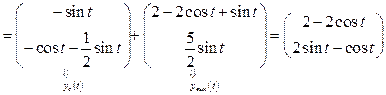 .
.
Третий способ. Использование теоремы Кели-Гамильтона [60].
Рассмотрим два случая ее применения.
1. В случае различных собственных значений матрицы 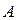 :
:
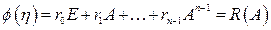 (1.59)
(1.59)
где 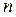 — число строк матрицы
— число строк матрицы 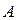 ;
; 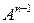 —
— 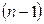 — я степень матрицы
— я степень матрицы 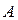 ; коэффициенты
; коэффициенты 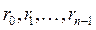 многочлена
многочлена 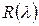 находятся из системы уравнений
находятся из системы уравнений
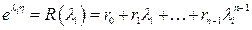 ,
, 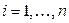 . (1.60)
. (1.60)
2. В случае кратных собственных значений матрицы 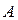 формула (1.59) также справедлива. Корню
формула (1.59) также справедлива. Корню 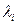 кратности
кратности 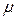 в системе
в системе 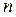 уравнений (1.60) соответствуют соотношения
уравнений (1.60) соответствуют соотношения
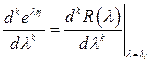 ,
, 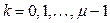 . (1.61)
. (1.61)
Пример 1.26. Найти переходную матрицу системы, если матрица 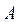 в уравнении состояния имеет вид
в уравнении состояния имеет вид 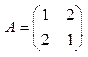 (см. пример 1.24).
(см. пример 1.24).
□ Собственные значения матрицы 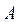 :
: 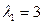 ,
,  различны,
различны, 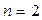 . Поэтому составим систему уравнений (1.60):
. Поэтому составим систему уравнений (1.60):
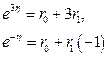 .
.
Отсюда 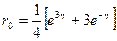 ,
, 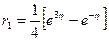 . По формуле (1.59) имеем
. По формуле (1.59) имеем
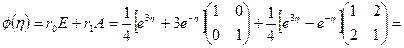
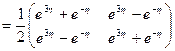 .
.
Результат совпадает с полученным ранее.■
Пример 1.27. Найти законы изменения векторов состояния и выхода многомерной системы:
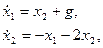
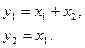
с начальными условиями 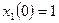 ,
, 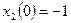 при входном сигнале
при входном сигнале
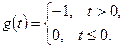
□ Перепишем уравнения системы в матричной форме:
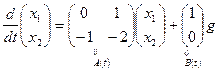 ,
, 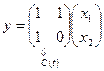 ,
,
где 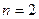 ,
, 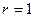 ,
, 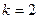 .
.
2. Найдем переходную матрицу. Для этого определим собственные шачения матрицы 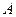 . Получим
. Получим
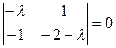 ,
, 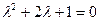 .
.
Отсюда 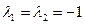 (корень действительный кратный). По формуле (1.61) имеем
(корень действительный кратный). По формуле (1.61) имеем
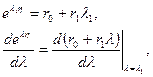 т.е.
т.е. 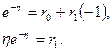
Отсюда 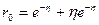 ,
, 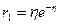 . По формуле (1.59) получаем
. По формуле (1.59) получаем
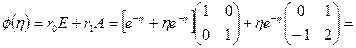
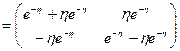 .
.
3. По формулам (1.51), (1.52) найдем законы изменения векторои состоя ния и выхода:
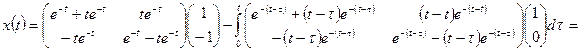
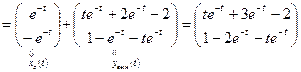 ,
,
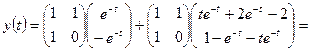
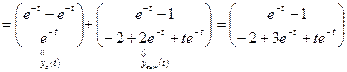 .
.
Дата добавления: 2017-09-01; просмотров: 1817;











