Метод сплайнов 1-го порядка (нахождения точки глобального минимума)

Будем рассматривать задачу

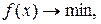
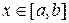, (1)

где 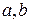– некоторые числа ( ).

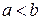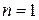Определение.Сплайном некоторой функции 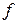на 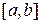называют некоторую непрерывную функцию, состоящую из кусков функций заданного класса и аппроксимирующую исходную функцию снизу.

Если в качестве кусков выбирается линейная функция, то сплайн представляет из себя некоторую ломаную и называется сплайном 1-го порядка.

Если в качестве кусков выбирается квадратичные функции (куски парабол), то говорят о сплайне 2-го порядка.

Метод состоит в следующем: пусть дана задача (1), задана 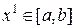– начальное приближение.

Предполагаем, что выполняется условие

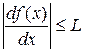(2)

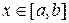, (то есть тангенс угла наклона касательной находится на 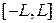). Пусть одновременно с реализацией метода задана некоторая процедура поиска. (То есть по некоторому принципу на 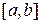выбираются точки. Эти точки подставляются в целевую функцию и находится рекорд и рекордный план.)

1-ая итерация: по 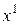строится простейший сплайн

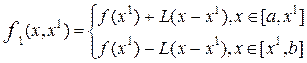
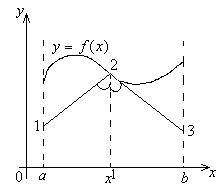
На рисунке сплайн ломаная 1-2-3. Простейший сплайн 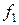представляет из себя ломаную 1-2-3, причём угловой коэффициент [1,2]= 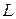, а [2,3]= 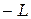. Так как выполняется неравенство (2), то 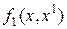аппроксимирует снизу функцию 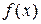, (лежит не выше неё), затем решаем задачу 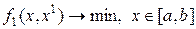и пусть 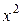– оптимальный план этой задачи. Затем производится анализ.

a

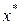Пусть – рекордный план, тогда если 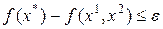, где 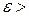0 – малое (требуемая точность вычислений), тогда рекордный план принимается за 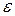-оптимальное.

В противном случае переходим ко 2-ой итерации: строим сплайн. Сначала по 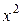– простейший

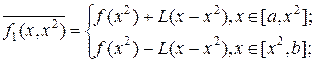
Затем 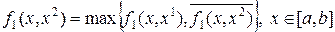и решается задача 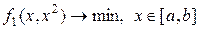, её решение принимается за .

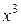Затем совершается анализ: если 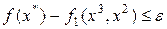, то рекордный план 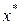принимается за приближённое решение, в противном случае 3-я итерация и так далее.

Опишем 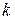-ую итерацию: пусть построена точка 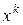и сплайн 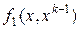тогда строим простейший сплайн по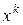

;

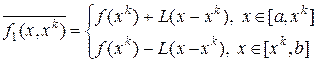затем 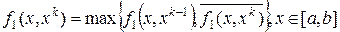. Затем рассматривается задача 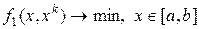и решение принимается за .

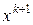Анализ: если выполняется неравенств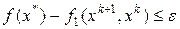о , то 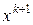служит приближённым значением задачи, в противном случае приходим к 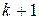-итерации.

Замечание. Обычно при реализации схемы перебора 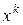включаются в неё и перебираемые планы и они выбираются из окрестности этой точки.

Последовательность 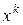сходится к оптимальному плану: 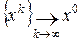– оптимальный план задачи (1).

С ростом итераций сплайн всё точнее описывает целевую функцию 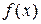в окрестности точки минимума.

Чем точнее подобрано 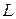в (2), тем быстрее сходится метод.

Замечание. Если в методе вместо линейных сплайнов использовать квадратичные (по определённым 3-м точкам строятся куски парабол с ветвями направленными вверх и вниз в зависимости от кривизны), то приходим к методу сплайнов 2-го порядка, которые точнее аппроксимируют функцию 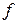в окрестности оптимального плана. Этот метод быстрее сходится.