В прямоугольной декартовой системе координат

Одним из уравнений системы для определения переменных параметров нефти, газа или их смеси и параметров пласта является общее дифференциальное уравнение движения сжимаемой жидкости или газа в упругой среде уравнение неразрывности (сплошности) фильтрационного потока. Оно выражает баланс массы жидкости в пределах постоянного элементарного объема, выделенного внутри пористой или трещиноватой среды.

Выделим в фильтрующей среде элементарный параллелепипед с ребрами 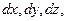параллельными координатным осям (рис. 24). Объём выделенного параллелепипеда обозначим через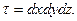

Рис. 24. Элемент фильтрующей среды с прямыми рёбрами.

Объём порового пространства внутри параллелепипеда 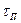можно написать так:

,

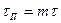где 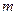— коэффициент пористости, являющийся переменной величиной.

Найдём изменение массы жидкости внутри нашего параллелепипеда за промежуток времени 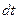, производя расчет двумя различными способами.

Пусть масса жидкости, заполняющей поры выделенного элемента пласта, будет равна М.Тогда 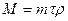, (VIII.1)

где 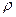— плотность жидкости.

Дифференцируя (VIII.1), найдём изменение массы М за промежуток времени :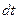

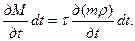(VIII.2)

С другой стороны, положим, что через грань 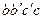параллелепипеда втекает жидкость, причем массовая скорость фильтрации равна 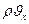;. За время 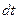через площадь грани 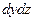протекает масса 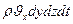. Через противоположную грань 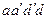которая отстоит от первой на расстояние 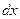, протекает за то же время масса

.

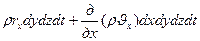Накопленная в параллелепипеде за время 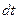масса составляет разность между массами втекающей и вытекающей жидкостей:

.

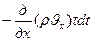Аналогичные выражения получим для избыточной массы, образовавшейся в нашем элементе пористой среды за время 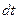при фильтрации жидкости вдоль осе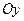й и 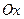соответственно:

,

.

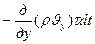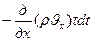Суммируя три последних выражения, найдём полную массу жидкости, накопленную в элементе пористой среды за время 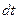при условии, что источниками и стоками жидкости являются исключительно внешние грани выделенного параллелепипеда, т. е. что внутри нашего элемента не существует источников и стоков:

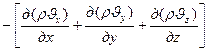
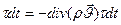, (VIII.З)

где 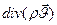— символическая запись дифференциального трёхчлена в квадратных скобках левой части; ( div — первые три буквы латинского divergere — “обнаруживать расхождение”; 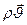— вектор массовой скорости фильтрации.

Приравнивал выражения (IV.2) и (IV.3), получим уравнение неразрывности фильтрационного потока:

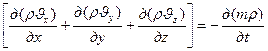(VIII.4)

Для несжимаемой жидкости 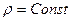и, следовательно, уравнение (IV.4) принимает вид:

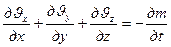(V.4a)

Уравнение (VIII.4) — одно из дифференциальных уравнений системы, необходимой для решения задач. К числу уравнений этой системы относятся уравнения, выражающие закон фильтрации жидкости (например, закон Дарси), а также уравнения состояния жидкости и фильтрующей среды.

В уравнении неразрывности находит своё выражение закон сохранения массы.

Дифференциальный трёхчлен левой части уравнения неразрывности (VIII.4) иногда обозначают так:

= .

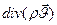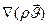При этом уравнение неразрывности запишется короче:

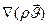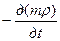= (VIII.5)

Символ 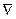(“набла”) называют оператором Гамильтона.

Как и при течении жидкости в трубах или в открытых руслах, движение жидкости в фильтрующей среде может быть установившимся (стационарным) и неустановившимся (нестационарным). При установившейся фильтрации величины плотности жидкости 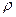, скорости фильтрации 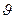и пористости породы 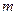в каждой данной точке пористой среды являются неизменяемыми и, следовательно, не зависящими от времени.

Таким образом, при установившейся фильтрации имеем:

,

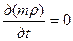в результате чего уравнение неразрывности (IV.4) запишется так:

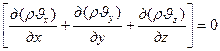(VIII.6)

или 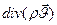=0

Если фильтруется несжимаемая жидкость в недеформируемом пласте, будем иметь

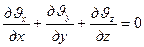. (VIII.6a)