Представление графов в ЭВМ

Наиболее распространены следующие 4 метода представления графов в ЭВМ:

- Матрица смежности,

- Матрица инцидентности,

- Списки смежности вершин,

- Списки смежности дуг.

Вы уже имеете представление о представлении графа матрицами смежности и инцидентности (Тема 11, пункт 1). Поясним суть списков смежности вершин.

Списки смежности вершин – представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой.

Представление графа с помощью массива структур представляется в виде записей: .

Тема 12. Компоненты связности и объединение графов. Оценка числа ребер через число вершин и число компонентов связности. Вершинная и реберная связность. Мосты и блоки.

Объединение графов и компоненты связности. Оценка числа рёбер через число вершин и число компонентов связности. Вершинная и рёберная связность: мосты и блоки, меры связности.

Напомним, что если граф G состоит из одной компоненты связности, (то есть k(G) = 1), то он называется связным.

В связном графе любые две вершины соединены (простой) цепью.

Теорема: Граф связен тогда и только тогда, когда его нельзя представить в виде объединения двух графов.

Рассмотрим граф:

V k1 k2

Замечание: Несвязный граф можно всегда представить как объединение связных компонент. Эти компоненты можно рассматривать независимо.

Вершина графа называется точкой сочленения, если ее удаление увеличивает число компонент связности.

В любом нетривиальном графе есть, по крайней мере, две вершины, которые не являются точками сочленения.

Теорема:Пусть р – число вершин, q – число ребер, k – число компонент связности графа. Тогда (p-k) ≤ q ≤ (p-k)(p-k+1) / 2.

Следствие: Если q > (p-1)(p-2) / 2 , то граф связен.

Мостом называется ребро, удаление которого увеличивает число компонент связности.

Рассмотрим рисунок:

w c d

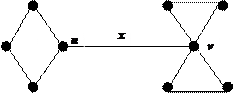
b e f

u, v – точки сочленения, х – ребро-мост, awb, buw, awub, cdv, evf – блоки.

Блоком называется связный граф, не имеющий точек сочленения.

Если в графе есть мост, то есть и точка сочленения. Концы всякого моста кроме висячих вершин являются точкой сочленения, но не всякая точка сочленения является концом моста.

Вершинной связностью графа G (обозначается x(G)) называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу.

Пример:

æ(G) = 0, если G несвязен;

æ(G) = 1, если G имеет точку сочленения;

Граф G называется k-связным, если æ(G) = k.

Реберной связностью графа G (обозначается A(G)) называется наименьшее число ребер, удаление которых приводит к несвязному или тривиальному графу.

Пример:

λ(G) = 0, если G несвязен;

λ(G) = 1, если G имеет мост;

λ(К_р) = р-1, значит, граф К_р– полный.

<20 21 222324 25 26 >

Дата добавления: 2021-07-22; просмотров: 490;