Действия над отношениями
Пусть 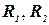 ‑ два отношения с одинаковым диапазоном. Тогда пересечением
‑ два отношения с одинаковым диапазоном. Тогда пересечением 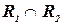 называется отношение, содержащее все наборы значений переменных, которые имеются одновременно в обоих отношениях
называется отношение, содержащее все наборы значений переменных, которые имеются одновременно в обоих отношениях 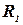 и
и 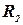 .
.
Объединение 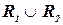 ‑ отношение, содержащее все наборы значений переменных, которые имеются либо в
‑ отношение, содержащее все наборы значений переменных, которые имеются либо в 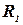 , либо в
, либо в 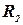 , или в обоих отношениях.
, или в обоих отношениях.
Разностью 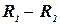 называется отношение, содержащее наборы значений переменных, содержащиеся в
называется отношение, содержащее наборы значений переменных, содержащиеся в 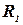 , но не содержащиеся в
, но не содержащиеся в 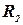 .
.
Проекция 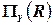 отношения
отношения 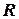 на множество переменных
на множество переменных 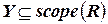 является отношением, содержащим наборы значений только переменных, содержащихся в
является отношением, содержащим наборы значений только переменных, содержащихся в 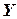 . В табличном представлении отношений проекция выбирает подмножество столбцов, соответствующих множеству
. В табличном представлении отношений проекция выбирает подмножество столбцов, соответствующих множеству 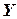 .
.
Соединение отношений. Оператор соединения 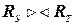 из двух отношений
из двух отношений 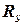 с диапазоном
с диапазоном 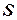 и
и 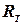 с диапазоном
с диапазоном 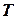 строит новое отношение, состоящее из их общих переменных в
строит новое отношение, состоящее из их общих переменных в 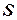 и
и 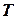 . Набор
. Набор 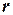 из соединения
из соединения 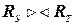 отношений
отношений 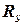 и
и 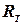 можно построить, используя следующие шаги: (1) взять набор
можно построить, используя следующие шаги: (1) взять набор 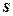 из
из 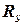 ; (2) выбрать набор
; (2) выбрать набор 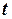 из
из 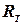 такой, что компоненты
такой, что компоненты 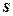 и
и 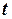 согласуются по переменным из
согласуются по переменным из 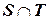 , общим для
, общим для 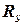 и
и 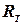 ; (3) образовать новый набор
; (3) образовать новый набор 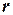 , комбинируя компоненты
, комбинируя компоненты 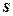 и
и 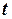 , сохраняя лишь один из полученных одинаковых наборов. Диапазон получающегося отношения ‑
, сохраняя лишь один из полученных одинаковых наборов. Диапазон получающегося отношения ‑ 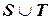 . Соединение двух отношений с одинаковыми диапазонами эквивалентно пересечению этих отношений.
. Соединение двух отношений с одинаковыми диапазонами эквивалентно пересечению этих отношений.
Виды ограничений
Рассмотрим различные виды ограничений. Простейшим типом ограничения является унарное ограничение, которое ограничивает значение единственной переменной. Каждое унарное ограничение можно устранить, выполняя предварительную обработку области определения соответствующей переменной, чтобы удалить значения, нарушающие это ограничение. Бинарное ограничение связывает между собой две переменные, например, 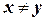 . Бинарной задачей УО называется задача, в которой имеются только бинарные ограничения; она может быть представлена в виде графа ограничений. В ограничениях высокого порядка участвуют три или больше переменных. Одним из известных примеров таких задач являются криптоарифметические головоломки, называемые также числовыми ребусами (см. раздел 10.1.2). Обычно накладывается требование, чтобы каждая буква в криптоарифметической головоломке представляла отдельную цифру. В случае задачи SEND+MORE=MONEY из примера 10.7 раздела 10.1.2, такое требование может быть выражено с помощью ограничения с восемью переменными all-different(S, E, N, D, M, O, R, Y). Иным образом это требование может быть представлено в виде набора бинарных ограничений, таких как
. Бинарной задачей УО называется задача, в которой имеются только бинарные ограничения; она может быть представлена в виде графа ограничений. В ограничениях высокого порядка участвуют три или больше переменных. Одним из известных примеров таких задач являются криптоарифметические головоломки, называемые также числовыми ребусами (см. раздел 10.1.2). Обычно накладывается требование, чтобы каждая буква в криптоарифметической головоломке представляла отдельную цифру. В случае задачи SEND+MORE=MONEY из примера 10.7 раздела 10.1.2, такое требование может быть выражено с помощью ограничения с восемью переменными all-different(S, E, N, D, M, O, R, Y). Иным образом это требование может быть представлено в виде набора бинарных ограничений, таких как 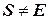 .
.
Дата добавления: 2016-06-05; просмотров: 1930;











