Машинное представление графов и сетей.

<123 4 5 6 7 >

Задать граф (орграф) — значит описать множества его вершин (узлов) и ребер (дуг), а в случае взвешенного графа или сети, описать также функцию весов с: Е→R.

Мы будем предполагать, что вершины графов и узлы сетей занумерованы натуральными числами от 1 до n. Поэтому для описания множества вершин (узлов), если не указана какая-нибудь дополнительная информация, достаточно задать одно число — число вершин (узлов) n.

Для представления множества ребер (дуг) имеется много различных способов. Мы разберем здесь лишь основные из них. Но вначале сформулируем условия, по степени выполнения которых определяют, удачно или неудачно то или иное представление графа (орграфа).

1. Требуемый объем памяти.

2. Удобство доступа к информации для ответа на вопросы:

a) имеется ли в графе (орграфе) ребро {v,w} (дуга (v,w))?

b) к каким вершинам (узлам) ведут ребра (дуги) из V?

c) какова степень вершины (узла) v?

3. Удобство доступа к информации для осуществления следующих процедур:

a) добавить к графу (орграфу) ребро {v,w} (дугу (v,w));

b) удалить из графа (орграфа) ребро {v,w} (дугу (v,w));

Разберем несколько способов машинного представления графа (орграфа) G = (V,E), где n= |V |, m= | Е |.

Матрица смежностей. Она определяется как матрица А размера n 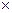n, в которой A[v,w]=l тогда и только тогда, когда ребро {v,w} (соответственно дуга (v,w)) имеется в графе (орграфе), и A[v.w]=0 в противном случае.

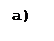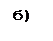А= А=

Рис 2.3. а) Неориентированный граф и его матрица смежностей,

б) Ориентированный граф и его матрица смежностей.

Легко видеть, что матрица смежностей неориентированного графа является симметричной.

Представление графа матрицей смежностей удобно для тех алгоритмов, которым многократно нужно выяснять, есть ли в графе ребро (дуга), соединяющее заданные вершины v и w, ибо это осуществляется за один шаг — одно обращение к матрице. Матрица смежностей удобна и в том случае, когда многократно нужно корректировать граф, добавляя в него или удаляя из него ребра. Поэтому сточки зрения пунктов 2.а, З.а, З.б представление графа матрицей смежностей является очень хорошим. Однако, для ответа на вопросы 2.6 и 2.в нужно просмотреть всю строку матрицы с номером v. Следовательно, сложность ответа на любой из этих вопросов для фиксированной вершины есть О(n).

В целом, можно сказать, что матрица смежностей является достаточно удобным способом представления графа, если не принимать во внимание затраты памяти: граф на n вершинах требует памяти пропорционально n², независимо от числа ребер. Особенно сильно этот недостаток проявляется для разреженных графов, т.е. таких, в которых число ребер невелико по сравнению с числом вершин: в этом случае матрица смежностей почти целиком состоит из нулей.

Взвешенный граф (или сеть) G = (V,E,c), может быть задан в ЭВМ матрицей весов А. в которой полагают A[v,w] = c({v,w}) - весу ребра {v,w} (или весу дуги c((v,w)) ), и A[v,w] = ∞ — для ребер (дуг), отсутствующих в графе (сети). Иногда, в зависимости от специфики конкретной задачи, уточняют знак бесконечности, выбирая либо +∞, либо - ∞.

Более экономным, чем матрица смежностей, и в некотором смысле, универсальным способом является представление графов и сетей списками смежностей.

Списком смежностей для вершины (узла) v называется список всех вершин (узлов) w, смежных с v. Граф (орграф) представляется с помощью п списков смежностей: по одному для каждой вершины (узла). Точнее, каждый элемент такого списка является записью r, имеющей два поля. Первое поле, обозначим его r^{^}.строка, предназначается для хранения вершин, смежных данной; второе — r^{^}.след — для ссылки на следующую запись в списке. При этом будем считать, что r^{^}.след = nil для последней записи в списке.

Начало каждого списка хранится в массиве НАЧАЛО, а именно, HAЧAJIO[v] является указателем на начало списка, соответствующего вершине (узлу) v; если v — изолированная вершина (узел), то полагаем HAЧAЛО[v] = nil. Весь такой список для неориентированного графа будем обозначать ЗАПИСЬ[v]. Ясно, что в этом случае каждое ребро (v, w) графа представлено дважды: вершиной w в списке ЗАПИСЬ[v] и вершиной v в списке ЗАПИСЬ[w].

НАЧАЛО

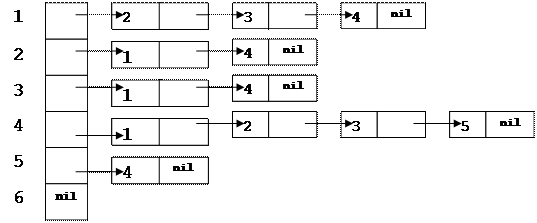Рис 2.3. Неориентированный граф и его списки смежностей.

Для ориентированных графов возможны два способа формирования списков смежностей. В первом в список ЗАПИСЬ[v] включаются лишь те узлы w, для которых (v, w) E, т.е. те узлы, к которым ведут дуги из w. Такой список будем обозначать СЛЕД[v]. Другой способ — включать в список ЗАПИСЬ[v] лишь те узлы w, из которых идут дуги в узел v. Этот список будем обозначать ПРЕДШ[v].

Для представления взвешенного графа или сети достаточно в соответствующих списках смежностей отвести одно дополнительное поле для весов ребер или дуг.

Проанализируем теперь способ представления графов и сетей списками смежностей.

Понятно, что объем памяти, необходимый для представления графа или сети, имеет порядок n+m, что, вообще говоря, лучше, чем представление матрицей смежности. Особенно заметным этот выигрыш по памяти становится для редких графов (m ˂˂ n²).

Ограничимся далее случаем неориентированного графа. Для ответа на вопросы 2.а, 2.б, 2.в достаточно просмотреть список ЗАПИСЬ[v]. Сложность такого просмотра есть О(n) — такая же, как и в случае матрицы смежностей Однако, если определять степень всех вершин графа, то здесь сложность ответа будет O(n+m), так как каждое ребро смотрится ровно два раза, в то время как для матрицы смежностей вычислительная сложность такого просмотра есть О(n²).

Списки смежностей являются достаточно удобным инструментом для решения задач добавления или удаления ребер из графа. Осуществляются подобные процедуры стандартными средствами для работы со списками. Понятно, что сложность процедуры добавления ребра является константой, если известно, что данного ребра в графе нет, и имеет сложность О(n), если предварительно требуется осуществить поиск для ответа на вопрос о том, есть или нет данное ребро в графе. Аналогично обстоит дело и с процедурой удаления ребра (дуги) из графа (соответственно орграфа).

В тех случаях, когда нет необходимости добавлять и удалять ребра или дуги из графа, все списки смежностей вместе с массивом НАЧАЛО можно упаковать в один массив, называемый массивом смежностей.

Массив смежностей представляет собой одномерный массив А длины (n+2m+2) для неориентированного графа, и (n+m+2) — для ориентированного.

Рассмотрим случай неориентированного графа. Первые n+1 элементов массива А являются адресной частью, а именно, значением A[v] (v=l,2,...,n) является адрес (индекс) в массиве А, начиная с которого в А записаны подряд все вершины, смежные с вершиной v; А[n+1] указывает на конец массива.

Поскольку каждое ребро графа встречается в таком массиве дважды (и имеет индексы в массиве от А[n+2] до А[n+1]-1), то массив действительно имеет длину n+2m+2. Отсюда следует, что этот способ представления графа требует меньше памяти, чем матрица смежностей и чем списки смежностей (так как в последнем случае нет нужды в храпении ссылок на следующие записи). Для ориентированных графов в массиве смежностей, так же как и в списках смежностей, можно хранить дуги по одному разу, записывая либо только исходящие дуги, либо только входящие. И в том, и в другом случае массив будет иметь длину n+m+2 .

I

A[I] Nil

Nil

Рис. 2.4. Неориентированный граф и его массив смежностей

Массив смежностей не только экономен по требуемой памяти, но и очень удобен для ответов на запросы раздела 2. Действительно, чтобы узнать, есть ли в графе ребро {v,w}, достаточно просмотреть массив А от A[v] до A[v+1], Сложность такого просмотра есть О(n).

Еще проще выяснить степень заданной вершины v: она равна A[v+1]-A[v] (разумеется, в предположении, что соответствующие значения отличаются от nil). Одним словом, этот способ исключительно удобен, если нет нужды в корректировке графа. Понятно, что добавить или удалить ребро графа, заданного массивом смежностей, равносильно переиндексации всего массива А, что является весьма трудоемким занятием.

В случае ориентированного графа вместо массива смежностей удобно вводить либо массив СЛЕД, либо массив ПРЕДШ, которые определяются способом, аналогичным спискам СЛЕД и ПРЕДШ.

ЗАДАЧИ

1. Докажите, что в любом графе число вершин нечетной степени четно.

2. В некоторых задачах удобно представлять граф связанными списками смежностей. А именно, каждая запись в списке 3AПИСЬ[v] имеет еще одно поле, где в записи, содержащей вершину w, в дополнительном поле ставится ссылка на ту запись тиски 3AПИСЬ[w], которая содержит вершину v. Напишите алгоритмы удаления и добавления ребра в граф, заданный связанными списками смежностей.

3. Предложите алгоритм, сложности О(n), записывающий все вершины в списке ЗАПИСЬ[v] в обратном порядке.

4. Пусть некоторый граф задан матрицей смежностей. Рассмотрим следующую процедуру:

1. begin х:=0;

2. for р:=1 to n do

3. for q:=p to n do

4. х:= х + A[p,q];

5. end.

Чему будет равен х в результате работы этой процедуры?

Глава III

Сортировка данных

Задача сортировки формулируется следующим образом: дана последовательность из n элементов a₁,...,a_n, выбранных из множества, на котором задано отношение линейного порядка. Требуется найти перестановку s = (s(l),…,s(n)) индексов, для которой a_s₍₁₎ ≤ a_s₍₂₎ ≤ ... ≤ a_s₍_n₎, т.е. расположить элементы данной последовательности в неубывающем порядке (или в невозрастающем, т.е. a_s₍₁₎ ≥ a_s₍₂₎ ≥ ... ≥ a_s₍_n₎).

Сортировка — практически важная и теоретически интересная задача. Она является неотъемлемой частью многих алгоритмов решения задач дискретной оптимизации. Решая задачу сортировки, мы введем полезную структуру данных — представление массива в виде двоичного дерева данных. Такая структура представляет самостоятельный интерес и часто используется на практике.

<123 4 5 6 7 >

Дата добавления: 2021-07-22; просмотров: 391;