Сложность задачи сортировки

Рассмотрим задачу сортировки в общем виде, когда информа­цию о последовательности элементов можно получать только с помощью операции сравнения двух элементов. Пусть а₁,...,а_n - последовательность сортируемых элементов. Не ограничивая общности, можно считать, что элементы заданной последовательности помещены в некоторый массив А в том же порядке, m есть A[i] = a, (i = 1,2,...,n).

Начнем с простейшего алгоритма сортировки данных, называемого алгоритмом сортировки выбором. Формализованное описание этого алгоритма представлено ниже.

АЛГОРИТМ 3.1. СОРТИРОВКА ВЫБОРОМ

Данные: массив А[1..n].

Результат: массив А[1..n] такой, что А[1] ≤ А[2] ≤ ... ≤ A[n].

1. begin

2. procedure MIN(i):

3. begin for j = i to n do

4. if A[i] < A[j] then A[i]↔A[j];

5. end;

6. begin (* главная программа *)

7. for i := 1 to n-1 do MIN(i);

8. end;

9. end.

Алгоритм 3.1 имеет следующую структуру. Процедура MIN(i) выбирает минимальный элемент из массива а_i,...,а_n и ставит его на первое место, т.е. на место a_i. Алгоритм начинает работу с вы­зова процедуры MIN(l), которая перемещает на первое место наименьший элемент исходного массива. Далее процедура по­вторяется для массива а₂,...,а_n и т.д.

Теорема 3.1.Алгоритм СОРТИРОВКА ВЫБОРОМ имеет вы­числительную сложность O(n²).

□ Действительно, в процедуре MIN(i) осуществляется (n-i) операции сравнения и, в худшем случае, (n-i) операции обмена. Значит, общее число шагов, выполняемое процедурой MIN(i) пропорционально (n-i). Отсюда, число шагов алгоритма пропор­ционально (n - 1) + (n — 2) + ... + 1 = n(n - 1 )/2, то есть сложность алгоритма есть O(n²).

Легко видеть, что число сравнений в алгоритме СОРТИРОВ­КА ВЫБОРОМ в точности равно n(n- 1)/2 , т.е. имеет порядок n²,как и сложность всего алгоритма. Ситуация эта не случайна, так как мы рассматриваем задачу сортировки в предположении, что информацию об элементах можно получать только с помо­щью операций сравнения. Поэтому в дальнейшем, оценивая сложность того или иного алгоритма, будем учитывать только операции сравнения, поскольку именно они и определяют слож­ность алгоритма.

Следующая теорема дает оценку снизу сложности любого ал­горитма сортировки.

Теорема 3.2.В любом алгоритме, упорядочивающем с помо­щью сравнений, на упорядочение последовательности из n эле­ментов тратится не менее c∙n∙loqn сравнений при некотором с > 0 и достаточно большом n.

Любой алгоритм, упорядочивающий с помощью сравнений, можно схематично представить в виде корневого дерева (см. па­раграф 2.1.), называемого двоичным деревом решений. Это дере­во можно рассматривать как блок-схему алгоритма сортировки, в котором показаны все сравнения элементов и исходы алгоритма. Вершины дерева (кроме листьев) соответствуют сравнениям эле­ментов, при этом корень дерева соответствует первому сравне­нию, осуществляемому алгоритмом. Сыновья вершин изобража­ют возможные исходы сравнения отца. Листья соответствуют исходу алгоритма.

На рис 3.1 изображено дерево решений алгоритма СОРТИ­РОВКИ ВЫБОРОМ для сортировки последовательности из трех элементов а₁,а₂,а₃. Здесь запись а:b означает сравнение элементов а и b. После сравнения а и b идем по левой дуге при а ≤ b и по правой при а ≥ b.

Вообще говоря, исходом работы алгоритма явится последова­тельность из трех элементов такая, что а₁ ≤ а₂ ≤ а₃, однако окон­чательное значение а₁ может (за счет операции переприсваивания) отличаться от исходного. На рис. 3.1 листья изображают возможные исходы относительно начальных значений перемен­ных.

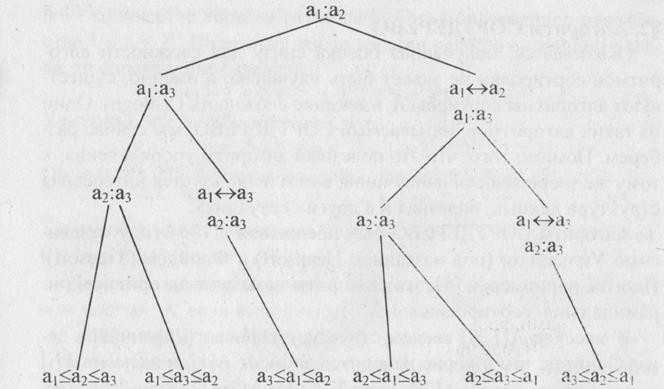Рис. 3.1. Двоичное дерево решений для сортировки трех элементов

В любом таком дереве решений каждая перестановка опреде­ляет единственный путь от корня к листу. Поскольку алгоритм сортировки должен различать все возможные перестановки, по­лучаем, что дерево решений должно содержать как минимум n! листьев.

При каждом входе алгоритм проходит весь путь от корня до листа, соответствующего данному входу. Следовательно, число операций сравнения, осуществляемое алгоритмом, равно длине пути от корня до листа, то есть равно высоте двоичного дерева решений. Таким образом, высота этого дерева дает оценку снизу сложности алгоритма.

Поскольку, всякое двоичное дерево высоты к имеет не более 2^к листьев (лемма 2.1), то получаем, что должно выполняться не­равенство 2^к > n!, так как листьев в двоичном дереве решений должно быть не меньше, чем перестановок из n элементов. От­сюда, k > logn!. Осталось заметить, что при n > 1 справедлива следующая цепочка неравенств:

n! ≥ n(n - 1 )(n - 2)... ( 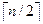) ≥ (n/2)^n/2, так что

log n! ≥ log( n/2 )^n/2 = n/2 log n/2 ≥ n/4 log n

Итак, k ≥ n/4 logn — полученное неравенство завершает дока­зательство теоремы 3.2.