Алгоритмы и их сложности


По устоявшейся терминологии различают массовые и индивидуальные задачи. Все вышеприведенные примеры дают образцы именно массовых задач. Индивидуальная задача получается из массовой путем фиксации набора условий. Например, индивидуальная задача коммивояжера получается из массовой, если зафиксировано число городов и определены затраты на переезды между всеми парами городов.

С каждой конкретной массовой задачей (в дальнейшем просто задачей) будем связывать некоторое число (или несколько чисел), называемое ее размером, которое выражает меру количества входных данных. Например, размером задачи коммивояжера естественно считать число городов n, которые собирается посетить путешественник.

Под алгоритмом решения задачи понимается общая, шаг за шагом выполнимая процедура решения задачи. Отметим, что имеется много формализаций понятия алгоритма, но их рассмотрение выходит за рамки данного пособия. Для определенности можно считать, что указанная процедура является программой для ЭВМ. Говорят, что алгоритм решает некоторую массовую задачу, если он решает любую ее индивидуальную задачу

Как оценить качество работы алгоритма? Почему мы говорим, что алгоритм полного перебора для решения, например, задачи о кратчайшем пути, вообще говоря, плох? Ведь решение задачи такой алгоритм обеспечивает, по крайней мере, теоретически.

Для оценки качества алгоритмов имеется много критериев. Одним из важнейших таких критериев является понятие вычислительной сложности (или просто сложности) алгоритма.

Неформально, под сложностью алгоритма решения массовой задачи будем понимать максимально возможное число шагов, выполняемых алгоритмом для решения любой из индивидуальных задач, вычисленное как функция размерности задачи.

Под шагом алгоритма будем понимать выполнение "простой" операции, обычно аппаратно реализованной на любой ЭВМ, а именно любой арифметической операции, операции сравнения, пересылки, косвенной адресации и т.п. Ясно, что при таком определении шага сложность алгоритма зависит от конкретного вида машинных команд. Однако нас никогда не будет интересовать точная сложность алгоритма, а только асимптотическая сложность, т.е. порядок роста числа шагов алгоритма, когда размерность задачи неограниченно растет.

При сравнении скорости роста двух неотрицательных функций f(n) и g(n) будем использовать следующие понятия.

Будем говорить, что функция f(n) имеет порядок роста не более чем g(n) (запись: f(n) = О(g(n))), если существуют константы с. N > 0 такие, что f(n) < cg(n) для всех n > N.

Говорят, что функция f(n) имеет порядок роста не менее чем g(n) (запись: f(n) = Ω (g(n)) ), если существуют константы с, N > 0 такие, что f(n) ≥ c g(n) для всех n > N.

Например, справедливы следующие соотношения:

log2n = О(n); n2 = 0(2n); n = Ω (log2n):

На практике алгоритм решения некоторой задачи считается достаточно хорошим, если сложность этого алгоритма есть O(np) при некотором р > 0. В этом случае говорят, что задача полиномиалъно разрешима, или, что то же самое, задача может быть решена за полиномиальное время.

Отметим, что как задача о кратчайшем пути, так и задача оптимального назначения относятся к классу полиномиально разрешимых. В то же время для задачи коммивояжера неизвестен алгоритм решения, имеющий полиномиальную сложность, впрочем, нет и доказательства того, что такой алгоритм не существует. Однако, для задачи коммивояжера, как и для целого ряда других естественно формулируемых задач, известно, что если будем найден алгоритм ее решения, имеющий полиномиальную сложность, то тем самым будут найдены полиномиальные алгоритмы и для очень обширного круга задач дискретной оптимизации. Такие задачи называют NP-полными. Проблема, заключающаяся в том, имеет ли хотя бы одна NP-полная задача (например, задача коммивояжера) алгоритм ее решения полиномиальной сложности, является одной из самых интересных и актуальных проблем современной математики. Рассмотрение вопросов, относящихся к теории NP-полных задач, не входит в рамки данного пособия. Читателя, заинтересовавшегося данной проблематикой, мы адресуем к книге М.Гэри и Д.Джонсона [2].

Важность понятия сложности алгоритма хорошо иллюстрируют следующие таблицы, заимствованные из книги А.Ахо, Дж.Хопкрофта, Дж.Ульмана [1].

Первая таблица построена в предположении, что один шаг работы алгоритма требует для своего выполнения 1 миллисекунду. Как следует из таблицы, при увеличении времени с 1 секунды до I часа, т.е. в 3,6*103 раз, размер задачи, решаемой алгоритмом сложности 2n, увеличивается только в 21/9 раза, а для алгоритма сложности п ровно в 3,6*103 раз.

Может показаться, что рост скорости вычислений, вызванный появлением новых ЭВМ, уменьшит значение эффективных (т.е. имеющих "небольшую" сложность) алгоритмов. Однако, как это видно из таблицы 1.1, в действительности происходит в точности противоположное. Так как ЭВМ работают все быстрее и возможно решение задач все большей размерности, именно сложность алгоритма определяет то увеличение размера задачи, которое можно достичь с увеличением скорости ЭВМ.

 

Сложность алгоритма Максимальный размер задачи
за 1 сек. за 1 мин за 1 час
n 6*104 3,6*106
n*log2n 2105
n2
n3
2n

Таблица 1.1. Максимальная размерность задач, разрешимых за данное время

 

Сложность алгоритма Размер наибольшей задачи, разрешимой за единицу времени
На современных ЭВМ На ЭВМ, в 10 раз более быстрых На ЭВМ, в 1000 раз более быстрых
n К 10К 1000К
n*logn L Почти 10L для больших L Почти 1000L для больших L
n2 М 3.I6M 31,6М
n3 N 2,15N 10N
2n Р Р+3,3 Р+9,97

Таблица 1.2. Влияние технического совершенствования ЭВМ на полиномиальные и экспоненциальные алгоритмы

 

Пусть для решения некоторой задачи имеется алгоритм сложности n3. Тогда, как это следует из таблицы 1.2, десятикратное увеличение скорости быстродействия ЭВМ позволит увеличить размер задачи, решаемой за 1 минуту в 2,15 раз. Однако замена этого алгоритма другим, имеющим сложность n2, позволит решать задачу в 6 раз большего размера (см. таблицу 1.1). Если в качестве единицы взять 1 час, то сравнение будет еще более впечатляющим.

Отметим, что для алгоритма сложности 2n десятикратное увеличение скорости ЭВМ увеличивает размер задачи, которую можно решить только на три единицы, тогда как для алгоритма сложности n2 размер задачи более чем утраивается, а для алгоритма сложности n происходит десятикратное увеличение допустимого размера разрешимости задачи.

 

Запись алгоритмов

Мы будем предполагать, что читатель знаком, хотя бы в общих чертах, с каким-нибудь языком программирования высокого уровня. Алгоритмы будем записывать на некотором специальном языке, который назовем упрощенным Паскалем, являющимся неформальной версией языка Паскаль.

Упрощенный Паскаль отличается от всех принятых языков программирования тем, что он разрешает использовать, любой тип математических предписаний, если только их значения понятны, а перевод в операторы Паскаля или любого другого языка высокого уровня очевиден. В этом языке возможно использование любого типа данных: тип данных какой-либо переменной и ее область действия должны быть ясны либо по ее названию, либо по контексту.

В упрощенном Паскале применяются традиционные конструкции математики и языков программирования такие, как выражения, условия, операторы и процедуры. Операторы языки Паскаль используются, как правило, в соответствии с правилами языка Паскаль, но иногда будут применяться неформальные конструкции такие, как, например, циклы for х ϵ X do Р, т.е. выполнять оператор Р для всех элементов х множества X в произвольной последовательности: x[ij ↔ x[j] — переставить i-ый и j-ый элементы массива; или описание типа: "пусть х — наименьший элемент множества X".

Будем также предполагать, что все операторы, записанные в одной строке алгоритма, образуют один составной оператор. Поэтому ключевые слова beginи end,идентифицирующие этот оператор, будут опускаться.

Предполагается, что читатель знаком с такими структурами данных, как массивы, списки, очереди и стеки. При работе с очередями и стеками будем использовать следующие обозначения:

СТЕК 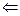х — поместить значение переменной х в стек;

х 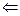СТЕК — переменной х присвоить значение вершины стека

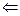СТЕК — удалить вершину стека;

ОЧЕРЕДЬ 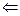х — включить х в очередь;

х 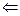ОЧЕРЕДЬ — переменной х присвоить значение первого элемента очереди;

ОЧЕРЕДЬ — удалить первый элемент очереди.

Строки алгоритма будем обычно нумеровать с тем, чтобы можно было указать на "цикл 10", "блок 7." и т.п.

С тем, чтобы пояснить только что сказанное, разберем легкий пример. Пусть требуется написать алгоритм, который по задан­ному числовому множеству X, выдает значение минимального элемента этого множества — minX. Вот, например, как можно это сделать.

 

АЛГОРИТМ 1.1. ВЫБОР МИНИМАЛЬНОГО ЭЛЕМЕНТА

Данные: числовое множество X.

Результат: число minX - минимальный элемент X

1. begin

2. minX := +∞;

3. for х ϵ X do

4. if x < minX then minX := x;

5. end.

Разумеется, читателя не должен смущать оператор присваивания, стоящий в строке 2. Здесь имеется в виду, что переменной minX присвоено самое большое машинное число. Если множество X задано в виде массива с именем X длины n то строки 3 и 4 алгоритма могут быть записаны так:

3'. for i:=1 to n do

4'. if X[i] < minX then minX:= X[i]:

Поясним на этом же примере понятие сложности алгоритм Размером этой задачи естественно считать n — количество элементов во множестве X. Цикл в строках 3-4 работает ровно n раз. В строке 4 при каждом шаге цикла осуществляется одна операция сравнения и, в худшем случае, одна операция присваивания. Таким образом, в строках 3 и 4 проводится не более чем 2n операций. С учетом оператора присваивания в строке 2 получаем, что число шагов алгоритма не превосходит 2n+1. Значит сложность этого алгоритма есть О(n).

Алгоритмы такой сложности принято называть ничейными.

Повсюду в дальнейшем будем использовать следующие обозначения. Для произвольного вещественного числа х через |_x_|(читается дно х) и |¯х¯| (потолок х) будем обозначить соответственно наибольшее целое число, не превосходящее х, и наименьшее целое, не меньшее х. Например, |_2,5_| = 2, |_-2,5_| = -3, |_3,2_| = 4, |_-3,2_| = -3.

Все логарифмы, встречающиеся в пособии, являются логарифмами чисел по основанию 2. поэтому вместо log2x будем писать logx. Символ обозначает начало и конец доказательства какого – либо утверждения.

Глава II

Графы и сети

Многие задачи дискретной оптимизации могут быть интерпретированы как задачи на сетях и графах. В этой главе мы введем основные понятия теории графов и рассмотрим способы представления сетей и графов в ЭВМ.

 

Графы, сети

Под неориентированным графом (или короче графим) будем понимать произвольную пару G = (V,E) конечных множеств V и Е таких, что Е 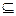{{v,w} : v,w V, v ≠ w}. Здесь и далее запись {v,w} обозначает неупорядоченную пару элементов v и w.

Элементы множества V будем называть вершинами графа G. а элементы Е — ребрами графа G. Если е = {v,w} — ребро графа, то вершины v и w будем называть концами ребра е, а ребро е — инцидентным вершинам v и w. Две вершины графа v и w назы­ваются смежными, если есть ребро в графе, их соединяющее, т.е. {v,w} Е.

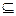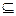Ориентированным графом (или короче орграфом) будем называть произвольную пару G = (V, E) конечных множеств V и E такую, что Е {(v,w) : v,w V,v≠w} V 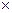V. Здесь и далее запись (v,w) обозначает упорядоченную пару элементов v и w. Говоря об орграфе, элементы множества V будем называть узлами орграфа, а элементы Е дугами Если е = (v,w) — дуга орграфа, то будем говорить, что v начало дуги е, w — конец дуги е, и. что дуга е исходит из узла v и входит в узел w.

 

 

       
   
 
 

 


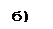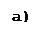Рис. 2.1. Изображение графов и орграфов, а) Неориентированный граф, б) Ориентированный гриф

Графы и орграфы обычно изображаются на плоскости и им и множества точек, соответствующих вершинам или узлам, и множества линий, соединяющих эти точки, которые соответствуют ребрам или дугам. Линия, изображающая ребро {v,w} или дугу (v,w), соединяет точки, изображающие вершины v и w, причем в случае ориентированного графа эта линия снабжается стрелкой, обозначающей направление от v к w. Удобно вершины графа считать пронумерованными натуральными числами, и на рисунках сразу вместо точки ставить соответствующий номер

Число ребер, инцидентных данной вершине, называется степенью вершины. Вершины степени 1 называют висячими вершинами, а степени 0 — изолированными. Например, в графе, изображенном на рис. 2.1.а, вершины 2, 5, 6 являются висячими и вершина 7 — изолированной.

Степенью захода узла в некотором орграфе называется число дуг, в нее входящих, степенью исхода — из нее исходящих. Под степенью узла будем понимать сумму степеней исхода и захода данного узла. Например, в орграфе, изображенном на рис. 2.1.б, степень исхода узла 1 равна 2, а степень захода — 1.

Цепью (соответственно путем) в графе (орграфе) G = (V,E) назовем чередующуюся последовательность вершин и ребер (узлов и дуг) v0,e0,V1, ... ,ek-1, vk такую, что каждое ребро ek соединяет вершины vk и vk+1 (соответственно исходит из vk и входит в vk+1). Вершины (узлы) v0 и vk будем называть соответственно началом и концом цепи (пути). Если все вершины (узлы) цепи (пути) различны, то такую цепь (путь) будем называть простои цепью(простым путем).

Цепь в графе (соответственно путь), начальная и конечная вершины (узлы) которого совпадают, будем называть циклом {контуром). Если в цикле (соответственно в контуре) все проме­жуточные вершины различны, то такой цикл (контур) будем на­зывать простым.

Иногда нам будет удобно цепь (путь) v0,e0,v1, ... , ek-1,vk отожде­ствлять с множеством ребер (дуг) е0, ... , ek-1 или вершин (узлов) v0,v1, ... ,vk, ее (его) образующих. Длиной цепи (пути) будем назы­вать число входящих в нее ребер (дуг).

Подграфом графа (орграфа) G = (V,E) будем называть произ­вольный граф (орграф) G' = (V',E') такой, что V' 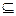V и 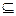Е' Е.

Пусть G=(V,E) — произвольный неориентированный граф и пусть v V. Пусть V' — множество тех вершин w V, к которым существует цепь из вершины v. Множество V' вместе с ребрами графа G, инцидентными вершинам из V', определяет некоторый подграф графа G, называемый связной компонентой графа G, содержащей данную вершину v.

Легко доказать, что множества вершин различных компонент связности произвольного графа попарно не пересекаются. На­пример, для графа, изображенного на рис. 2.1.а, это множества V1, = {1,2,3,4}, V2 = {5,6}, V3,= {7}.

Граф, имеющий ровно одну компоненту связности, будем на­зывать связным. Непосредственно из определения вытекает

 

Предложение 2.1.Неориентированный граф G=(V,E) связен тогда и только тогда, когда для любых вершин v,w V существу­ет цепь в графе G, их соединяющая.

Для орграфа G (V.E) через G*=(V*,E*) обозначим неориенти­рованный граф, для которого V*=V и {v,w} Е* тогда и только тогда, когда либо (v,w) E, либо (w,v) Е. Иначе говоря, граф G* получается из орграфа G уничтожением ориентации дуг. Орг­раф G будем называть связным, если соответствующий граф G* связен.

Всюду в дальнейшем через |А| будем обозначать количество элементов конечного множества А. Говоря о некотором графе или орграфе G=(V,E), через n будем обозначать количество вер­шин (или узлов), а через m — количество ребер (или дуг), то есть будем полагать n=|V|, m=|E|.

Поскольку мы условились считать, что в графах и орграфах нет ребер вида {v,v} и дуг вида (v,v) (так называемых петель), и, что для любых v,w V существует не более одного ребра или не более двух дуг им инцидентных, то справедливы неравенства:

1. m ≤ n∙(n-1 )/2 — для неориентированных графов,

2. m ≤ n∙(n-l) — для орграфов.

Одним из важнейших понятий в теории графов является поня­тие дерева. Деревом называется связный неориентированный граф без циклов. Следующая теорема будет часто использовать­ся

 

Теорема 2.1.Пусть G = (V,E) — граф, n=|V|, m=|E|. Тогда сле­дующие условия эквивалентны:

1. G — дерево.

2. Для любых двух вершин u,vе V существует и притом единственная цепь, их соединяющая.

3. Граф G связен, и m=n-l.

4. Граф G не содержит циклов, и m=n-l.

5. Граф G не содержит циклов, и при соединении любых двух несмежных вершин ребром образуется ровно один цикл.

□ 1. 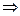2. Ясно, что если между некоторыми вершинами u и v имеется две цепи, то граф содержит цикл.

2. 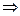3. Пусть v0,v1, ... ,vk — максимальная по включению цепь в графе G. Отсюда следует, что вершины v0 и vk — висячие вер­шины в графе G. Тем самым доказано, что всякий граф, удовле­творяющий условию 2. содержит хотя бы две висячие вершины.

Докажем теперь пункт 3 индукцией по n. Равенство m = n-1 для n=2 очевидно верно. Пусть равенство m = n-1верно для графов, у которых n= r. Докажем это равенство в случае n = r+1. Пусть v — висячая вершина графа G, и e={v ,w} — единственное ребро, инцидентное v. Удалим вершину v и ребро e из графа, т.е. рассмотрим граф G' = (V\{v), Е\{е}). Граф G', очевидно, также удовлетворяет условию 2, и количество вершин в нем равно r. По предположению индукции в графе G' имеется ровно r-1 ребро. Следовательно, исходный граф содержит r+1 вершину и r ребер, т.е. справедливо равенство m = n-1.

3. 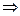4. Заметим, что связность графа не нарушится, если уда­лить любое ребро, входящее в какой-нибудь цикл графа. Предпо­ложим теперь, что граф содержит циклы. Удалим тогда любое ребро, входящее в какой-нибудь цикл. Граф останется связным, и если он вновь содержит циклы, то повторим процедуру удаления ребра, входящего в какой-нибудь цикл. Так будем действовать до тех пор, пока в графе не будут уничтожены все циклы. Поскольку связность при таком удалении ребер не нарушается, то получим дерево. Для деревьев справедливо равенство m = n-1, так как це­почка утверждений 1. 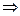2. 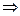3. уже доказана. Поскольку, по условию, равенство m = n-1 выполняется с самого начала, значит ни одного ребра мы не удаляли, т.е. граф не содержит циклов.

4. 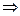5. Пусть G имеет k компонент связности Gi = (Vi, ,Еi), i = l,2,...,k. Тогда все графы G; являются деревьями, и, следова­тельно, для всех i = 1,…,k справедливы равенства mi = ni-i. Скла­дывая все эти равенства, получим

m1 + m2 +…+ mk = n1 + n2 +…+nk – k,

или m = n-k. Однако, по условию, m = n-1. Значит, k=l т.e. G — дерево. Поскольку в дереве между любыми вершинами сущест­вует ровно одна цепь, их соединяющая, то, как легко видеть, до­бавление любого ребра образует ровно один цикл.

5. 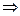1. Ясно, что из условия 5 сразу следует связность графа, т.е. G — дерево. □

 

Ориентированный граф без контуров называется корневым деревом, если

a) имеется в точности один узел, называемый корнем, в кото­рый не входит ни одна дуга (т.е. степень захода равна нулю);

b) в каждый узел, кроме корня, входит ровно одна дуга;

c) для каждого узла существует путь, начинающийся в корне и заканчивающийся в этом узле.

 

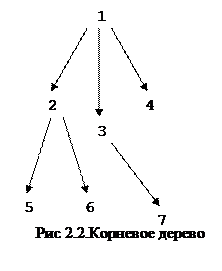Корневое дерево обычно изобра­жают корнем вверх, располагая узлы одной глубины на одном уровне. У корневого дерева на рис. 2.2 узел с номером 1 является корнем, узлы 4, 5, 6, 7 —- листья. Высота этого дерева равна 2.

 

Следующее утверждение является непосредственным следст­вием определения корневого дерева.

 

Лемма 2.1.Для каждого узла корневого дерева существует в точности один путь, начинающийся в корне и кончающийся в этом узле.

Пусть G - (V,E) — корневое дерево, v,w V. Будем говорить, что узел v является отцом узла w, a w — сыном узла v, если (v,w) Е. Если в G существует путь из v до w, то будем гово­рить, что w — потомок v, a v — предок w. Вершина, не имею­щая сыновей, называется листом. Глубина узла v в корневом дереве — это длина пути из корня в v. При этом глубину корня будем считать равной нулю. Высота узла v — это длина самого длинного пути из v в какой-нибудь лист. Высотой дерева будем называть высоту его корня.

Корневое дерево, каждый узел которого имеет не более двух сыновей, будем называть двоичным деревом. Методом математи­ческой индукции легко доказать следующее утверждение.

 

Лемма 2.2.Двоичное дерево высоты k содержит не более 2k листьев.

Специфика дискретных оптимизационных задач практически всегда предполагает, что, как ребра графов, так и дуги орграфов, снабжены некоторой числовой характеристикой. Практический смысл этих характеристик может быть самым разнообразным. Например, в задачах, сформулированных ранее в главе I, это были: длина дороги между соседними городами (задача о кратчай­шем пути), время обработки конкретной детали на конкретном станке (задача оптимального назначения), стоимость проезда из одного города в другой (задача коммивояжера).

Граф (орграф) будем называть взвешенным, если задана функ­ция с: Е→R, иначе говоря, каждому ребру (дуге) из Е поставле­но в соответствие вещественное число с(е). Число с(е) назовем весом ребра (дуги) е. Впрочем, в зависимости от специфики той или иной задачи дискретной оптимизации, число с(е) будем так­же называть стоимостью ребра (дуги) е, или пропускной способ­ностью ребра (дуги) е.

Ориентированный взвешенный граф будем называть сетью. Таким образом, взвешенный граф или сеть задаются тройкой G = (V,E,c).

 


Дата добавления: 2021-07-22; просмотров: 417;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.034 сек.