Устойчивость плавающих тел

Способность плавающего тела при нарушении равновесия возвращаться в положение равновесия при устранении причин, вызывающих отклонение, называется устойчивостью плавающего тела.

Понятие устойчивости может быть применено как к телам, полностью погруженным в жидкость (находящимся в подводном положении), так и к телам, плавающим на поверхности жидкости.

На тело, находящееся в жидкости, действуют сила тяжести и гидростатическая (архимедова) выталкивающая сила со стороны жидкости. Точка приложения силы тяжести тела – центр тяжести. Точкой приложения выталкивающей силы является центр давления D. Центр давления в общем случае не совпадает с центром тяжести тела C. Центр давления – это центр тяжести объема жидкости, вытесненной погруженной в жидкость частью тела. Его положение зависит от формы подводной части тела. Положение центра тяжести самого плавающего тела зависит от распределения в нем масс. В случае плавания судна положение центра тяжести определяется совокупностью масс корпуса судна, надстроек, установленного оборудования, груза, топлива, людей. Меняя расположение оборудования или груза, можно изменить положение центра тяжести судна.

Определим условия устойчивого плавания тел.

Рассмотрим случай подводного плавания тел (рис. 2.15).

В положении равновесия (рис. 2.15.а) центр давления D и центр тяжести C находятся на одной вертикали.

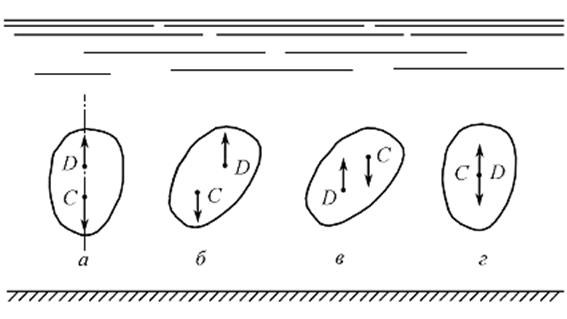
Рис. 2.15

При нарушении равновесного положения устойчивость плавающего тела зависит от взаимного расположения центра давления и центра тяжести:

· если центр давления D расположен выше центра тяжести C (рис. 2.15.б), то выталкивающая сила и сила тяжести создают момент сил, стремящийся вернуть тело в положение равновесия; следовательно, равновесие тела будет устойчивым;

· если центр давления D расположен ниже центра тяжести C (рис. 2.15.в), пара сил создает момент, увеличивающий отклонение тела от положения равновесия (опрокидывающий момент); устойчивость отсутствует;

· если точки приложения выталкивающей силы и силы тяжести совпадают (рис. 2.15.г), момента сил не возникает, тело продолжает находиться в положении безразличного равновесия, однако в исходное положение оно не возвращается.

Таким образом, устойчивостью при подводном плавании тело обладает только в случае, когда центр тяжести тела расположен ниже центра давления.

Для тел (судов), плавающих на поверхности жидкости, различают продольную и поперечную устойчивость. Различие заключается в плоскости отклонений из положения равновесия: при продольной устойчивости суда возвращаются в прямое положение из отклонений, происходящих в продольной диаметральной плоскости, то есть из дифферента, при поперечной устойчивости отклонения происходят в поперечной диаметральной плоскости, суда возвращаются в прямое положение из крена.

Рассмотрим условия поперечной устойчивости. Будем считать, что грузы на судне закреплены неподвижно, поэтому при крене судна положение его центра тяжести по отношению к корпусу остается неизменным. Иначе обстоит дело с центром давления. Напомним, что центр давления – это центр тяжести объема жидкости, вытесненной погруженной в жидкость частью тела, его положение зависит от формы подводной части тела. При крене судна меняется форма подводной его части и соответственно изменяется положение центра давления (рис. 2.16).

Как видно из рис. 2.16.а при наклоне судна грузовая ватерлиния AB переходит в положение 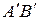. При этом клинообразный объем 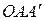корпуса судна переходит из подводного положения в надводное, а равный ему объем 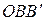уходит под поверхность воды. Общий объем вытесненной жидкости при этом не меняется, однако правая (погрузившаяся) половина корпуса вытесняет теперь жидкости больше, чем левая, симметрия нарушается. Поэтому центр давления D смещается с оси симметрии корпуса судна в сторону погрузившейся части (в точку 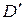). При малых углах крена (10° – 15°) смещение центра давления происходит таким образом, как если бы центр давления переместился по дуге окружности с центром в точке M, лежащей на оси корпуса судна.

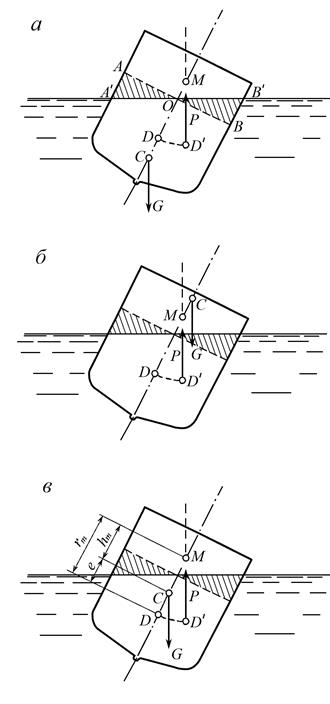
Рис. 2.16

Эта точка называется метацентром. При малых углах крена положение метацентра определяется пересечением линии действия архимедовой силы P с осью симметрии корпуса.

Если центр тяжести судна C расположен ниже центра давления D (рис. 2.16.а) при крене судна сила тяжести и подъемная сила образуют пару сил, которые стремятся возвратить судно в равновесное положение, судно устойчиво.

Если центр тяжести располагается не только выше центра давления, но и выше метацентра (рис. 2.16.б) сила тяжести и подъемная сила образуют пару, которая стремится перевернуть судно. Условия устойчивости не выполняются.

Если центр тяжести судна расположен выше центра давления, но ниже метацентра (рис. 2.16.в), образующаяся при крене пара сил возвращает судно в первоначальное положение, устойчивость обеспечена.

Таким образом, для обеспечения устойчивости судна требуется выполнение следующего условия: центр тяжести судна должен располагаться ниже метацентра.

У реальных судов при нормальных условиях работы обеспечивается именно случай, когда центр тяжести располагается выше центра давления, но ниже метацентра.

Расстояние между метацентром и центром давления r_m (рис. 2.16.в) называется метацентрическим радиусом, превышение метацентра над центром тяжести судна h_m называется метацентрической высотой. Напомним (формула (2.15)), что расстояние между центром тяжести и центром давления называется эксцентриситетом давления e.

Тогда условие устойчивости судна можно записать так:

e < r_m,

то есть эксцентриситет давления должен быть меньше метацентрического радиуса. Иначе говоря,

,

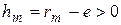метацентрическая высота должна быть величиной положительной.

Зная метацентрическую высоту и водоизмещение судна (определяемое величиной выталкивающей силы P) можно для каждого малого угла крена определить величину момента, возвращающего судно в положение равновесия:

,

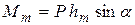где 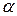– угол крена, 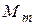– метацентрический момент.

Для углов крена больших 15° пользоваться этой формулой нельзя, так как при больших углах метацентр уже не лежит на оси симметрии плавания. Зависимость метацентрического момента от угла крена при больших 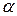определяют опытным путем и представляют в виде графика.

В случаях продольной устойчивости, то есть возвращении плавающих судов в прямое положение из дифферента, оказывается, что метацентрический радиус r_m всегда бывает большим, поэтому продольная устойчивость плавающих судов всегда обеспечивается.