Нагрузка на соединение
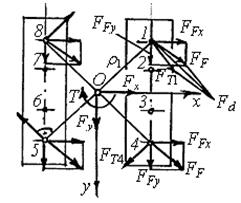
1. Определяют координаты центра масс О (рис. 2.8) плоскости стыка.
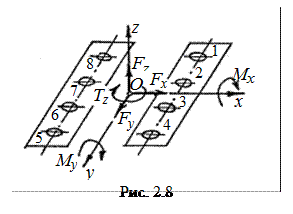
| 2. Число болтов z. Болты нумеруют в любой последовательности (1, 2… z). 3. Внешнюю нагрузку приводят к центру О и раскладывают на проекции по осям x, y, z. В самом общем случае нагружения будем иметь (рис. 2.8): – три проекции силы – Fx, Fy, Fz; – три проекции момента – Mx, My, Tz. Под действием Fx, Fy, Тz стык и болты испытывают сдвиг в плоскости стыка; под дей |
ствием Mx, My, Fz – отрыв в плоскости, перпендикулярной стыку. Прочность болтов на сдвиг и отрыв рассматривают раздельно.
4. Нагрузку FFj от центральных сил Fj, где j = x, y, z, считают распределенной по болтам равномерно:
FFj = Fj / z. (2.7)
2.3.2. Сдвиг соединения под действием Fx, Fy, Тz
В дальнейшем индекс z у Тz опускаем, т.е. Tz обозначаем Т.
|
FF = (Fx2 + Fy2)1/2. (2.8)
| Рис. 2.9 | 2. Принято допущение, что под действием момента Т соединение стремится повернуться вокруг центра масс. Нагрузка от момента Т распределяется по болтам пропорционально их расстояниям r от центра масс О и направлена перпендикулярно r. Из условия равновесия имеем Т = FT1r1 + FT2r2 + … + FTiri . (2.9) Из условия пропорциональности FT1 / r1 = FT2 / r2 = … = FTi / ri. |
Выразив силы FT2 , FT3 … FTi_ через FT1 –наибольшую по величине, находящуюся на наибольшем расстоянии r1 – FT2 = FT1r2 /r1 , …, FTi = FT1ri / r1, – и, подставив их в условие (2.9), получим
Т = FT1r12 /r1 + FT1r22 /r1 + … + FT1ri2 /r1.
Отсюда FT1 = Тr1 / (r12 + r22 + … + ri2). В общем виде для i-го болта
FТi = 103Тri / (Sri2) , (2.10)
где Т, Н×м; ri, мм; i = 1, 2…z.
3. При совместном действии силы FF и силы FТi определяют полную сдвигающую силу Fd, действующую на наиболее нагруженный болт. На рис. 2.9 это болт 1 – угол между векторами FF и FТ1 острый. Для него по теореме косинусов сдвигающая сила будет равна:
Fd1 = [FТ12 + FF2 – 2FТ1FFcos(FТ1ÙFF)]1/2.
4. Условием надежности соединения является отсутствие сдвига деталей в стыке под действием силы Fd.
Соединение может быть выполнено в двух вариантах:
а) на болтах, установленных в отверстия деталей с зазором;
б) на болтах (по ГОСТ 7817-80), установленных в отверстия плотно, без зазора.
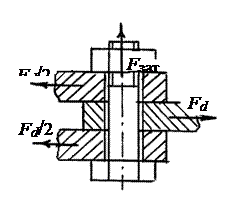
5. Болт с зазором.СилаFd уравновешивается силами трения Ff на стыках. Они создаются силой затяжки Fзат болта при сборке (рис. 2.10): Ff = iFзатf ³ Fd . Откуда требуемая сила затяжки
Fзат = KFd / (if), (2.11)
где К = 1,5…2 – коэффициент запаса затяжки на сдвиг; i – число плоскостей стыка; f – коэффициент трения материалов деталей на стыке.
 Если, например, принять К = 1,5, f = 0,15, i = 1, то требуемая сила Fзат должна быть в 10 раз больше внешней сдвигающей силы Fd . Отсюда большие
Если, например, принять К = 1,5, f = 0,15, i = 1, то требуемая сила Fзат должна быть в 10 раз больше внешней сдвигающей силы Fd . Отсюда большие
| размеры диаметров болтов, но этот способ самый простой и дешевый. Для уменьшения диаметров болтов применяют болты без зазора или устройства, разгружающие стык от силы Fd: например, штифты, шпонки, насечку на поверхностях, втулки, кольца, замковые уступы и др. 7. Болт без зазора. Сила Fd (рис. 2.11) воспринимается стержнем болта, который установлен плотно в отверстие из-под развертки (dC > d). Предва рительной затяжки болта для восприятия | Рис. 2.10 | ||
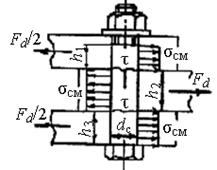
| силы Fd не требуется. Болты специальные по ГОСТ 7817-80. Они работают на срез и смятие. При расчете из условия среза определяют диаметр стержня dC dC¢ ³ [4Fd / (p[t]ср]1/2 с округлением до стандартного dC из условия dC ³ ≥ dC¢ и проверкой напряжений смятия по формуле sсм = Fd / (dCShmin) £ [s]см, где Shmin – наименьшая сумма толщин соединяемых деталей, сминаемых с одной стороны (на |
Рис. 2.11 |
рис. 2.11 – это h2 или h1 + h3).
2.3.3. Отрыв соединения под действием Fz, Mx, My
1. Нагрузка в зоне болта от центральной силы Fz:FF=Fz/z.
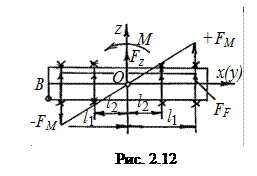 2. Сила FМ от изгибающих моментов М распределяется по болтам (рис. 2.12) пропорционально их расстояниям от центральных осей.
2. Сила FМ от изгибающих моментов М распределяется по болтам (рис. 2.12) пропорционально их расстояниям от центральных осей.
Из условия равновесия и пропорциональности сил FМi и расстояний li будем иметь для наиболее нагруженного болта (вывод аналогичен выводу формулы (2.10))
FМ 1 = 103Ml1 / (2m 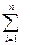 li2), (2.12)
где li – расстояние от центра масс до оси i-го болта с одной стороныот центральной оси, мм; li2), (2.12)
где li – расстояние от центра масс до оси i-го болта с одной стороныот центральной оси, мм;
|
n – число поперечных рядов болтов с одной стороныот центральной оси (множитель 2 в формуле (2.12) учитывает обе стороны); m – число болтов в одном поперечном ряду.
3. Суммарная внешняя осевая сила в зоне наиболее нагруженного болта
F = ± FF + FМxmax + FМymax ,(2.13)
|
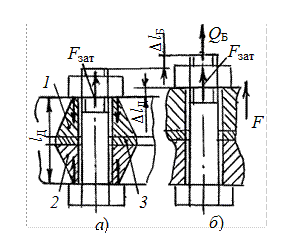
| Рис. 2.13 | 4. Возможность раскрытия стыка силой F устраняется предварительной затяжкой болтов Fзат . Применяют болты с зазором. При сборке соединения силой Fзат (рис. 2.13, а) стержень болта растягивается, а соединяемые детали сжимаются (условно считают в пределах конусов 1, 2 и цилиндра 3 сжатия). После приложения к деталям внешней силы F (рис. 2.13, б)болт дополнительно растянется на величину DlБ, а детали ослабят свое первоначальное сжатие на DlД (разгрузка стыка). |
Условие равновесия сил:
QБ + QД = F, (2.14)
где QБ – часть внешней нагрузки, приходящейся на болт, QД – часть внешней нагрузки, идущей на ослабление сжатого силой Fзат стыка.
Условие совместности деформаций болта DlБ и деталей DlД:
DlБ = DlД , (2.15)
где по закону Гука Dl = Ql / (EA) = Ql, здесь Е – модуль упругости материала; А – площадь поперечного сечения на длине l; l = l / (EA) – податливость, мм/Н.
Тогда из условия (2.14) QД = F – QБ и из условия (2.15) будем иметь QБlБ = (F – QБ)lД. Откуда QБ = FlД / (lБ + lД) .
Соотношение податливостей называют коэффициентом c основной(внешней) нагрузки: c = lД / (lБ + lД) .
Тогда QБ = cF и QД = (1 – c)F. Только часть внешней силыcF идет на дополнительное растяжение болта, остальная часть (1 – c)F расходуется на разгрузку сжатого стыка деталей (уменьшение силы затяжки в них).
Для жесткого стыка (стальные, чугунные детали) определено, что c =
= 0,2… 0,3. При наличии в стыке упругих прокладок (медь, алюминий, картон, резина и т.д.) c растет и стремится к единице. Если QД = Fзат или F = Fзат / (1 –
– c), то произойдет раскрытие стыка. Следовательно, чем больше сила затяжки Fзат , тем большая сила необходима для раскрытия стыка.
Расчетная сила на болт с учетом скручивания стержня при затяжке гайки:
FБ = 1,3 Fзат + cF . (2.16)
Сила затяжки
Дата добавления: 2021-07-22; просмотров: 557;