ДАВЛЕНИЕ НА ВЫКИДЕ НАСОСА И НАГРУЗКА НА ПЛУНЖЕР

При ходе штанги вверх, когда закрыт нагнетательный кла­пан, υ₀ = υ^в и Q= υ^в (F_пл - F_шт), получаем

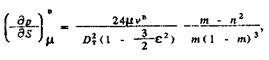(52)

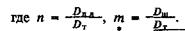
При 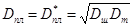перепад давления вследствие вязкого сопротивления отсутствует [3]. В этом случае расход опре­деляется количеством жидкости, увлекаемой штангами, а гра­диент давления - только гидростатическим слагаемым γ_см*соsα.

Если 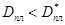, то градиент давления меньше гидроста­тического, а при 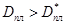больше гидростатического (по аб­солютным величинам).

При ходе штанг вниз υ₀ = - υ^н, закрытом всасывающем кла­пане Q_н = v^нF_шт

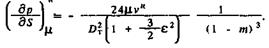(53)

В этом случае градиент давления всегда больше гидроста­тического. С помощью найденного отклонения оси штанги η(S) можно определить эксцентриситет в любой точке колонны штанг

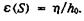
Так как градиент давления не очень сильно зависит от экс­центриситета, то для простоты вычислений примем для экс­центриситета некоторое постоянное значение 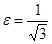, так что

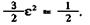
Тогда имеем

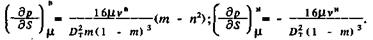(54)

Чтобы учесть дополнительные потери давления при обтекании муфт, можно также воспользоваться формулами (52) и (53). Примем для муфт ε = 1 и учтем, что l_м/l_ш ≈ 0,01. Тогда до­полнительное значение градиента давления, усредненное по длине штанги, равно

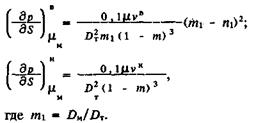(55)

Величины (55) сравним с (54) только для одного сочетани труб и штанг D_Г = 62 мм и D_ш = 25 мм. В остальных случая величины (55) можно не учитывать, и поэтому в общие формулы они далее не включаются.

Интегрируя (48) и (54) по длине колонны штанг, получай для давления на выкиде насоса

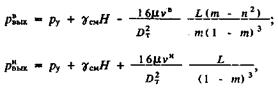(56)

где Н - глубина подвески насоса.

Выражения легко обобщаются на многоступенчатую колонну. Из условия статического равновесия плунжера определяем нагрузку на штанги в точке подвеса насоса:

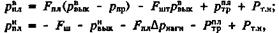(57)

где Р_пр - давление на приеме насоса; 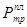- сила трения в плунжерной паре; Р_т.н. - вес тяжелого низа; ∆р_нагн - потеря давления в нагнетательном клапане насоса.

Сила вязкого сопротивления движению штанг может быть рассчитана с помощью вычисленного выше распределения скоро­стей (50) в зазоре между штангами и трубами. На единицу длины штанг действует сила

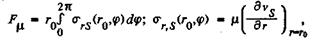
где σ_r,S (r₀,φ) - касательное напряжение на поверхности штанг.

С помощью (50) находим

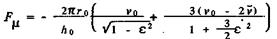(58)

Формулу нельзя использовать при ε→ 1, так как F_μ→ ∞.

Физический смысл этого результата в том, что при малом зазоре между штангами и трубой нельзя использовать модель Ньютона для жидкости. Случай ε = 1 соответствует касанию труб и штанг и рассматривался в разделе, посвященном граничному трению. Здесь примем ε = 0, тогда получаем

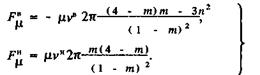(59)

При 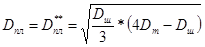сопротивление движению штанг вверх отсутствует. В этом случае градиент продоль­ной скорости υ_S в радиальном направлении, вызванный

движением штанг, равен по абсолютной величине и обратен по знаку градиенту скорости, вызванному расходом жидкости. При

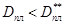сила сопротивления направлена противоположно движению. При 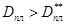расход жидкости настолько большой, что результирующая сила действует в направлении движения штанг. При движении колонны вниз сила сопротивления 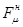всегда направлена против движения штанг. Чтобы учесть до­полнительное сопротивление при обтекании муфт, можно также воспользоваться формулами (59). Дополнительное сопротивление муфт, усредненное по длине штанги, можно рассчитать по формулам

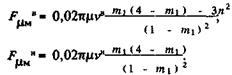(60)

Величины (60) следует учитывать только в случае исполь­зования штанг D_ш = 25 мм и труб D_т = 62 мм.