Условия работоспособности зубьев

<5 6 789 10 11 >

Напомним, что меньшее из пары зубчатых колес называется шестерней (z₁), большее – колесом (z₂). Параметры, относящиеся к шестерне, обозначают с индексом «1», к колесу – с индексом «2». Термин «зубчатое колесо» относят как к шестерне, так и к колесу.

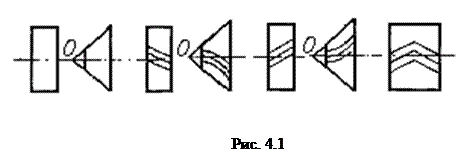На рис. 4.1 изображены направления наклонов линий зубьев и их названия: а) прямые зубья; б) правый наклон; в) левый наклон; г) шевронный наклон.

г)

в)

а)

б)

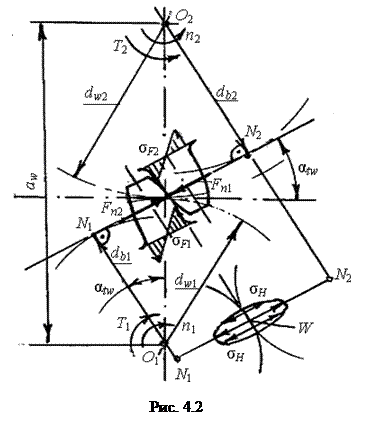
При передаче вращающего момента Т в зацеплении (рис. 4.2) действует нормальная сила F_n = 2000 Т / / d_b_{_}(d_b = d_wcosα_tw – диаметр основной окружности, где d_w – диаметр начальной окружности; α _t_w – угол зацепления), направленная по линии зацепления N₁N₂. По отношению к зубу колеса сила F_n₂ активна, т.е. движущая, и направлена в сторону вращения z₂, по отношению к зубу z₁ сила F_n₁реактивна (сила сопротивления колеса) и направлена против вращения шестерни. По закону Ньютона F_n₁ = F_n₂ = F_n. Деформацию зубьев под действием силы F_n рассматривают как сжатие двух цилиндров в плоскости заце

пления – задача Герца с первоначальным контактом по линии.

Кроме того, относительно заделки ножки зуба сила F_n действует на некотором плече, что вызывает изгибающий момент в основании зуба.

За счет скольжения поверхностей зубьев между ними возникает сила трения F_f = fF_n, где f – коэффициент трения скольжения.

Зуб испытывает сложное напряженное состояние. Решающее влияние на его работоспособность оказывают два основных напряжения: контактное σ_Н и

изгиба σ_F (“F” - Foot – ножка). Эти напряжения – переменные, изменяются по отнулевому циклу и приводят к усталостному разрушению зубьев. Число циклов изменения напряжений σ_Н и σ_F за один оборот равно с, где с – число зацеплений фиксированного зуба за один оборот.