Внешняя нагрузка и внутренние усилия

Рассмотрим прямой брус круглого поперечного сечения (рис.12.1,а), нагруженный внешними моментами m₁ и m₂, которые действуют в плоскостях, перпендикулярных к его оси и имеют разные направления действия. Такой брус называется валом и используется для передачи мощности от двигателя к разнообразным станкам или агрегатам. При условии, что m₁ = m₂ вал будет уравновешен относительно своей оси. На участке между плоскостями действия внешних моментов вал будет скручиваться, то есть одно поперечное сечение получит некоторый угол поворота относительно другого поперечного сечения. При этом в произвольном сечении этого вала возникнут внутренние моменты, которые имеют название крутящих моментов.

Выявить внутренние крутящие моменты и определить их величины позволяет известный метод сечений. Рассечем вал на две части плоскостью, перпендикулярной к его оси (рис.12,1,а). Разъединим эти части и каждую из них нагрузим соответствующими внешними моментами и неизвестными внутренними крутящими моментами М_кр. Последние должны быть направлены так, чтобы каждая часть вала находилась в равновесии. На рис.12.1,б и 12.1,в показанные крутящие моменты, которые действуют на каждую из частей вала. Из условия равновесия какой-либо части вала можно составить уравнение равновесия и определить величину и направление действия крутящего момента. Например, рассматривая равновесие левой отсеченной части вала (рис.12.1,б) и используя условие равновесия 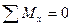, найдем: М_кр - m₁ =0, откуда М_кр = m₁

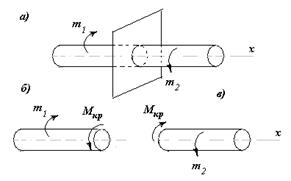
Рис.12.1

Если слева от сечения действуют несколько внешних моментов, то крутящий момент будет определяться алгебраической суммой этих моментов.

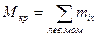(12.1)

Крутящий момент принимается с положительным знаком, если он действует против движения часовой стрелки относительно внешней нормали поперечного сечения вала. На рис.12.1,б М_кр имеет положительный знак.

Крутящий момент можно определить из условия равновесия правой отсеченной части вала. Используя условие 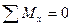, найдем:

М_кр- m₂=0, откуда М_кр= m₂. Если справа от сечения действует несколько внешних моментов, то крутящий момент будет определяться алгебраической суммой этих моментов, то есть:

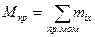(12.2)

В практических расчетах вала на прочность или жесткость, необходимо определить крутящие моменты на разных участках вала и построить эпюры этих моментов. Аналогично деформации растяжения стержня системой сосредоточенных сил, на участках вала, ограниченных плоскостями действия внешних моментов, крутящие моменты имеют постоянные значения, которые определяются по формулам (12.1) или (12.2).

Построим, например, эпюру крутящих моментов для вала, нагруженного тремя внешними моментами, если его правый торец закреплен с помощью жесткой опоры (рис.12.2,а).

Рассмотрим три участка вала, которые ограничены плоскостями действия внешних моментов, учитывая момент жесткой опоры. Этот момент можно не определять потому, что крутящие моменты на каждом участке можно определить, рассматривая последовательно участки от свободного (левого) торца вала.

Рассечем вал в пределах каждого участка произвольными поперечными сечениями 1-1, 2-2, 3-3, и составим уравнение равновесия его левых частей (рис.12.2,б,в,г), используя условие равновесия: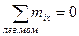

В результате получим: М_1кр - m₁ =0, откуда М_1кр = m₁= 2 кНм;

М_2кр = m₁ + m₂=2 +2 = 4 кНм;

М_3кр = m₁ + m₂ - m₃=2 +2 -6,5=2 +2-6,5 = -2,5 кНм;

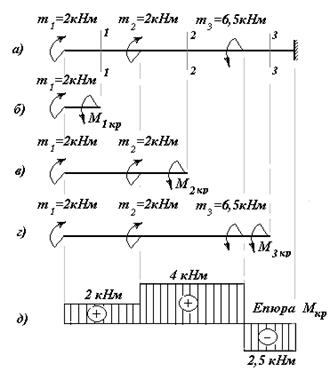
Рис.12.2

На рис.12.2,д построенная эпюра крутящих моментов, которая характеризует изменение этих моментов по длине вала.

Ордината эпюры крутящих моментов в опорном сечении вала равняется опорному моменту. В данном случае опорный момент равняется 2,5 кНм и действует в направлении часовой стрелки, если рассматривать вал от внешней нормали правого торца.

В рассмотренном выше примере внешние моменты были заданы и измерялись в килоньютонометрах. При решении практических задач на кручение задают чаще всего мощность N и угловую скорость вращения вала ω или n (скорость ω измеряется в радианах за секунду, а скорость n измеряется в количестве оборотов вала за минуту).

Если мощность, которая передается валу в некоторой плоскости (через некоторый шкив, насаженный на вал), задается в киловаттах, а скорость вращения ω в радианах за секунду, то внешний момент будет равняться:

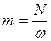(кНм). (12.3)

Если мощность, которая передается валу в некоторой плоскости, задается в киловаттах, а скорость вращения n в оборотах за минуту, то внешний момент будет определяться по формуле:

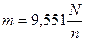(кНм) (12.4)

Выводы: 1) Кручением круглого вала называется такой вид его деформации, при котором в поперечных сечениях возникают лишь внутренние крутящие моменты;

2) Крутящий момент в произвольном сечении вала равняется алгебраической сумме внешних моментов, которые действуют по одну сторону от сечения (слева или справа);

3) Эпюра крутящих моментов имеет ступенчатую форму, то есть, ограничена прямыми линиями, параллельными оси вала. В сечениях вала, где действуют внешние моменты, эпюра крутящих моментов имеет скачки, которые равняются внешним моментам. Скачки направлены вверх или вниз, в зависимости от направления действия внешнего момента. Если вал рассматривать от левого торца и видеть, что внешний момент действует против часовой стрелки, то скачок эпюры будет направлен вверх. При действии внешнего момента по часовой стрелке скачок эпюры будет направлен вниз;

4) Эпюра крутящих моментов дает возможность определить расчетный крутящий момент. Он равняется наибольшей по модулю ординате построенной эпюры.