Расчет на контактную прочность
Согласно теории Герца - Беляева имеем
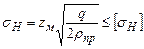 . (7.1)
. (7.1)
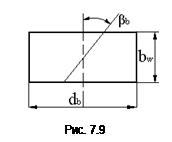
Т.к. в зацеплении косозубой передачи всегда работает более одной пары зубьев, то нагрузка распространяется на несколько зубьев. Суммарная длина контактных линий определяется
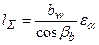 (рис. 7.9), тогда
(рис. 7.9), тогда 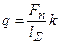
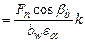 .
.
Так как 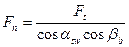 , а
, а 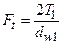 ,то окончательно имеем
,то окончательно имеем
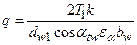 . (7.2)
. (7.2)
Определим теперь приведенный радиус кривизны. Расчет делаем в полюсе зацепления. Индекс «t» означает, что мы рассматриваем параметры зацепления в плоскости перпендикулярной осям колес. Из рис 7.10,а видно, что мы имеем 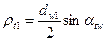 и
и 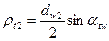 .
.
|

Рассмотрим основной цилиндр О с диаметром db. Выделим плоскость М, касательную к основному цилиндру по образующей АВ. Проведем в плоскости М прямую A'B'под углом bb к линии АВ. При обкатывании плоскости М без скольжения вокруг основного цилиндра прямая A'B'опишет эвольвентный профиль косого зуба. Выделим на эвольвентном профиле некоторую точку С (она лежит в полюсе зацепления).
Из рис. 7.10 следует, что
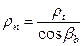 ,
,
где rn – радиус кривизны эвольвенты в плоскости нормальной поверхности зуба, rt – радиус кривизна эвольвенты в плоскости перпендикулярной оси цилиндра.
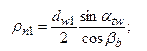
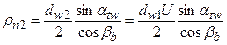 ,
,
тогда 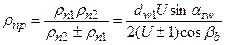 . (7.3)
. (7.3)
Подставляя уравнения (7.2) и (7.3) в уравнение (7.1), получим выражение для контактных напряжений в виде
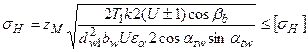 .
.
Обозначим 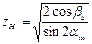 - коэффициент, учитывающий форму сопряженных поверхностей;
- коэффициент, учитывающий форму сопряженных поверхностей; 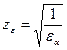 - коэффициент, учитывающий влияние торцевого перекрытия.
- коэффициент, учитывающий влияние торцевого перекрытия.
Использовав последние обозначения, окончательно получим выражение
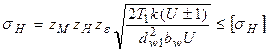 .
.
Эта формула отличается от формулы проверочного расчета высокоточных прямозубых колес только значениями zH и ze, поэтому обозначим их zHk и zek 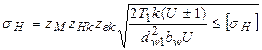 .
.
По аналогии, учитывая, что 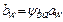 и
и 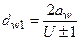 , получим
, получим
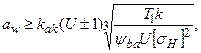
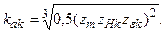
где
Это формула проектировочного расчета.
Дата добавления: 2017-03-12; просмотров: 1690;

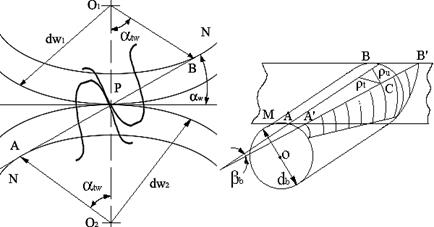 а б
Рис. 7.10
а б
Рис. 7.10










