Передачи коническими колесами
Конические колеса применяют в передачах с пересекающимися валами. Конические колеса выполняют с прямыми, косыми, круговыми и другими криволинейными зубьями. В настоящее время наибольшее распространение получили колеса конические с круговыми зубьями. Прямозубые колеса уместно применять при невысоких окружных скоростях (до 8 м/с). При высоких скоростях целесообразно применять колеса с круговыми зубьями как обеспечивающие более плавное зацепление, большую несущую способность и более технологичные.
Недостатки конических передач:
1) сложность изготовления;
2) сложность регулировки пятна контакта зубьев;
3) относительно низкий К.П.Д. (h к = 0,94…0,97).
Последнее объясняется тем, что при несовпадении вершин начальных конусов колес резко увеличивается скольжение в контакте зубьев. В связи с этим в конструкции редуктора должна быть предусмотрена возможность регулировки зацепления конических колес.
Элементы геометрического расчета
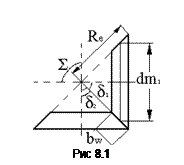
Угол между осями валов S, может быть любым, но наибольшее распространение получил угол S=900. Очевидно, что S=d1+d2, где d1 и d2– углы делительных конусов шестерни и колеса соответственно.
Внешнее конусное расстояние Re определяет габариты передачи (рис. 8.1).
Рабочая ширина зубчатого венца bw может быть выражена формулой
bw=ybd dm1=ybR Re,
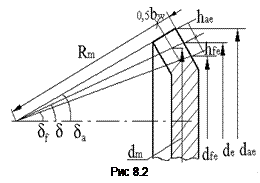
где ybd – коэффициент ширины шестерни относительно её делительного диаметра, 
– коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, dm – делительный диаметр в среднем сечении.
Вместо начальных и делительных цилиндров цилиндрических колес в конических колесах вводят понятия - начальный и делительный конуса, которые обладают теми же свойствами, что и делительные и начальные цилиндры. Все размеры зубчатого колеса определяются по наружному торцу:
hae= mte – внешняя высота головки зуба;
hfe= 1,2mte – внешняя высота ножки зуба;
mte – окружной модуль на внешнем торце;
df – угол конуса впадин зубьев;
da – угол конуса выступов зубьев;
de=mte z– диаметр внешней делительной окружности;
dae= de+2ha cosd – внешний диаметр окружности выступов;
dfe= de -2hf·cosd – внешний диаметр окружности впадин.
Под диаметром делительной окружности конического зубчатого колеса понимают диаметр основания делительного конуса колеса de= mte z=2Re sinδ,откуда
.
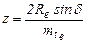Размеры зуба по длине различны, поэтому вводятся понятия о диаметре и модуле в среднем сечении:
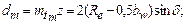
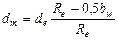
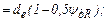
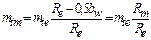, где Rm – среднее конусное расстояние.
Передаточное число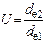 
, т.к. de1=2Re sind1 и de2=2Re sind2, то 
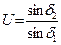. Для ортогональных передач, в которых S=900 , sind1 = cosd2 и U=tgd2=ctgd1.
Усилия в зацеплении
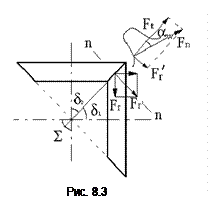Усилия в зацеплении рассмотрим на примере конической прямозубой передачи. Условно считаем, что все силы приложены в середине зуба на диаметрах dm1 и dm2 (см. рис. 8.3). В сечении плоскостью “n-n” нормальной поверхности зуба действует полное усилие Fn, которое раскладывается на окружное усилие Ft и усилие Fr'. В свою очередь усилие Fr' во фронтальной плоскости раскладывается на Fa (осевое усилие) и Fr (радиальное усилие). Для определения всех сил исходной является
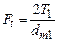
через него определяются усилия
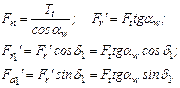
Для колеса направление сил противоположно, при этом
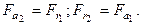
Эквивалентные колеса и определение их параметров
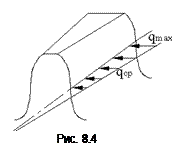Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса. Все поперечные сечения зуба геометрически подобны. При этом удельная нагрузка q (рис. 8.4) распределяется неравномерно по длине зуба. Она изменяется в зависимости от величины деформации и жесткости зуба в различных сечениях по закону треугольника, вершина которого совпадает с вершиной делительного конуса. Контактные и изгибные напряжения одинаковы по всей длине зуба. Это позволяет вести расчет на прочность по любому из сечений. Практически удобно принять за расчетные сечения среднее сечение зуба с нагрузкой qср.
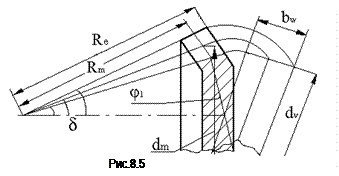
Для расчета на прочность конические колеса заменяют эквивалентными цилиндрическими, размеры которых определяются по развертке дополнительного конуса j, в среднем сечении (рис 8.5), при этом mtv = mtm.
Диаметр эквивалентного колеса
 |
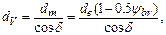
но
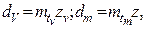получаем 
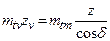, т.к mtv = mtm, то 
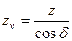, т. е.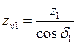 
.
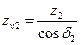Расчет на контактную прочность
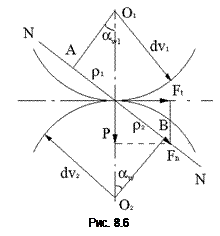Рассмотрим расчет конического колеса с прямым зубом и S=900. Расчет сводится к расчету эквивалентного цилиндрического колеса с прямым зубом (рис. 8.6). Опытом установлено, что коническое колесо все же менее прочно, чем цилиндрическое с размерами эквивалентного. Коническое колесо может передать в среднем 0,85 нагрузки цилиндрического с размерами эквивалентного, т. е.
bv=0,85bw.
По теории Герца - Беляева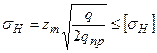 
.
Полная нагрузка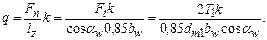 
Приведенный радиус кривизны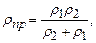 
где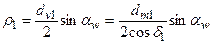 
;
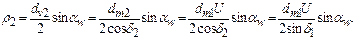
Запишем отношение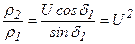 
, откуда 
.
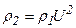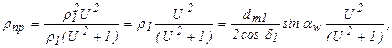
но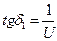 
или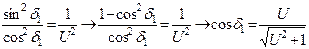 
.
Тогда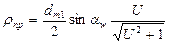 
.
После подстановки в формулу Герца - Беляева имеем
.
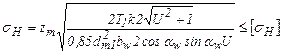Обозначим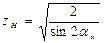 
- коэффициент, учитывающий форму сопряженных поверхностей, тогда имеем
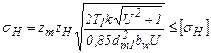
В проектировочном расчете bw=ybddm1. Возводим в квадрат обе части уравнения
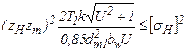или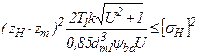 
.
Получаем, что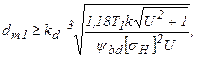 
где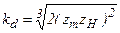 
- вспомогательный коэффициент.
Расчет на изгибную прочность зубьев конического колеса
Расчет сводится к расчету эквивалентного цилиндрического колеса.
Для цилиндрического колеса имеем выражение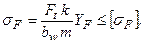 
Для проверочного расчёта после подстановки параметров конического колеса
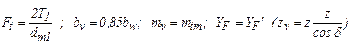получим
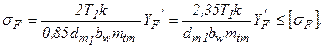
Для проектировочного расчета имеем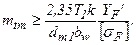 
Потери в зацеплении и определение КПД зубчатых передач
Потери мощности в зубчатых передачах в основном складываются из:
1) потерь на трение в зацеплении;
2) потерь на разбрызгивание масла;
3) потерь в подшипниках;
4) вентиляционных потерь (в особо быстроходных передачах).
Коэффициент полезного действия зубчатой передачи
h =1- Nr / N1,
где N1 – мощность на входе; Nr – мощность, потерянная в передаче.
Nr = NЗ +NГ +NП,
где NЗ, NГ, NП – соответственно мощности, потерянные на трение в зацеплении, на разбрызгивание и перемешивание масла (гидравлические потери), на трение в подшипниках.
Введем понятия
y З = NЗ /N1 – коэффициент потерь в зацеплении,
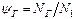- коэффициент гидравлических потерь,
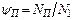- коэффициент потерь в подшипниках.
Тогда КПД можно записать
.
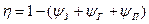Потери в зацеплении составляют главную часть потерь передачи и определяются как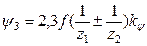 
,
где f – коэффициент трения; ky =1 – для некорригированной передачи;
ky =1,15…1,4 - для зацепления с высокой коррекцией.
Гидравлические потери растут с увеличением скорости, вязкости смазки, ширины колес, глубины погружения колес в масляную ванну. Они не зависят от нагрузки и поэтому относятся к числу так называемых постоянных потерь. Раздельное измерение потерь затруднено, поэтому измеряют суммарные потери в передаче.
Лекция №9
Червячные передачи
Общая характеристика
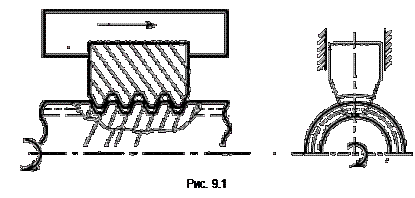Представление о работе червячной передачи можно получить, рассматривая кинематику резьбовой пары. Рассмотрим винт с трапецеидальной резьбой и сцепляющийся с ним сегмент гайки (рис 9.1).
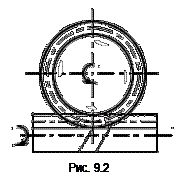
. При вращении винта сегмент гайки будет совершать поступательное движение в направляющих. Если взять сегмент гайки достаточно большой длины и согнуть его в кольцо, то получим зубчатое колесо, сцепляющееся с винтом и при вращении винта совершающее вращательное движение относительно своей оси. Такой механизм и называется червячной передачей (рис 9.2). Винт в ней называется червяком (ч), а колесо – червячным колесом (ч.к.). Движение червячной передачи преобразуется по принципу винтовой пары. В червячной передаче движение передаётся между скрещивающимися осями. Угол перекрещивания практически всегда равен 900. Этот вариант и будет рассматриваться в дальнейшем. Ведущим звеном обычно является червяк, но может быть и червячное колесо.
Червячные передачи по сравнению с зубчатыми передачами обладают следующими достоинствами:
1. Плавность и малошумность в работе;
2. Высокое передаточное отношение;
3. Возможность самоторможения (из-за трения движение от червячного к червяку не передаётся). Это свойство используется в подъёмных механизмах.
Недостатки червячной передачи:
1. 
Большие потери на трение, следовательно, большое тепловыделение и необходимость охлаждения;
2. Необходимость применения цветных металлов для снижения трения. Они дороги, следовательно, стоимость передачи высокая;
3. Сложность конструкции и, следовательно, повышенные эксплуатационные расходы. Это обусловлено необходимостью соблюдения высокой точности изготовления и сборки, а также необходимостью регулировки.
Типы червячных передач
Червячные передачи бывают двух типов:
а) цилиндрические (с цилиндрическим червяком) (рис. 9.3, а);
б) глобоидные (с глобоидным червяком) (рис. 9.3, б).
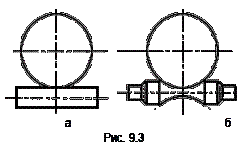В глобоидных передачах червяк как бы охватывает червячное колесо и увеличивает площадь контакта. При этом растёт нагрузочная способность в 2…4 раза. Технология изготовления этих передач значительно сложнее, поэтому их применение ограничено.
Цилиндрические червячные передачи в зависимости от формы зуба червяка бывают:
а) с архимедовым червяком;
б) с конволютным червяком;
в) с эвольвентным червяком.
Червяк, торцовым профилем которого является архимедова спираль,называется архимедовым червяком и его обозначают ZA. В осевом сечении он имеет трапецеидальный профиль и представляет собой обычный винт (рис 9.4).
Конволютный червяк (обозначение ZN1) в осевом сечении очерчен выпуклым профилем, в нормальном сечении А-А квинтовой линии – прямолинейный, а в торцовом сечении имеет профиль удлинённой эвольвенты.
Эвольвентный червяк (обозначаютZ1) в осевом сечении также имеет выпуклый профиль, а в торцовом сечении – эвольвентный.
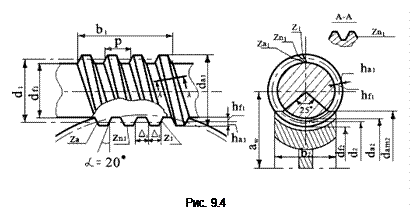
Он представляет собой, по существу, косозубое зубчатое колесо с очень большим углом наклона и малым числом зубьев. Архимедовы червяки имеют стандартный угол профиля a=200 в осевом сечении, конволютные в нормальном, а у эвольвентных – в нормальном сечении косозубой рейки, сцепляющейся с червяком. Нагрузочная способность червяков всех форм приблизительно одинаковая. Архимедов червяк может быть нарезан на обычных токарных и резьбофрезерных станках (не требуется специальных станков), однако шлифование его затруднено, так как необходим круг специального профиля. Поэтому архимедовы червяки широко применяют в передачах, где твёрдость червяка НВ<350. Конволютные червяки используют редко. Для их шлифования также требуется специальное профилирование шлифовального круга. Эвольвентные червяки применяют при необходимости высокой твёрдости (HRС > 45) и малой шероховатости поверхности. Они нарезаются и шлифуются инструментом с плоскими кромками путём обкатки, подобно зубчатым колёсам на специальных станках. Червячные колёса нарезаются червячными фрезами, которые являются копией червяка.
Дата добавления: 2017-03-12; просмотров: 1930;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
