Усилия в зацеплении
Усилие нормально поверхности зуба, т.е. действует по линии зацепления (в плоскости зацепления) и должно преодолевать момент сопротивления на колесе Т2 (рис. 7.5).
Рассмотрим зубчатое колесо в плане. Сделаем сечение плоскостью n-n нормально поверхности зуба. В плоскости n-n действует полное усилие Fn, которое дает на фронтальной плоскости, проекцию Ft'. Сила Ft' раскладывается в системе координат xoy на составляющие – окружное усилие Ft и осевое усилие Fa.
Повернем плоскость n-n на 90° в сторону чертежа. Здесь усилие Fn раскладывается на F't и Fr – радиальное усилие.
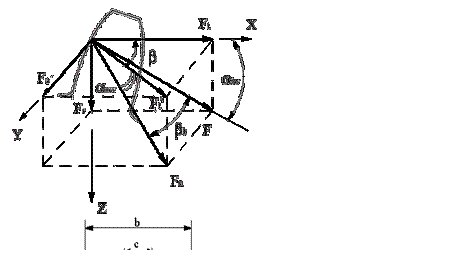
В системе координат xyz ( рис.7.6) разложение силы Fn принимает вид параллелепипеда. Сила Fn является диагональю параллелепипеда. Исходной всегда является сила Ft.
Усилия для косозубого зацепления можно записать в следующем виде:

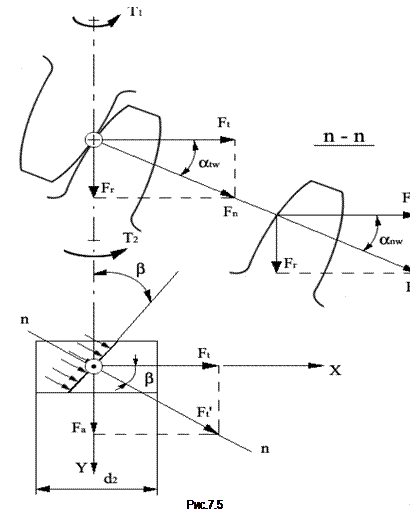

С увеличением b растет осевое усилие Fa, что является недостатком, т.к. дополнительно нагружаются опоры валов. С целью его уменьшения ограничиваются углы b = 8¸20°. Это не нужно делать на шевронных колесах.
Шеврон – это колесо с двумя зубчатыми венцами, на которых направление зубьев противоположно (рис.7.7). Осевые усилия здесь уравновешиваются на самом колесе. Для шевронных колёс значения угла наклона зубьев могут быть b = 30¸45°.
Понятие об эквивалентных колесах и определение их размеров
В косозубом цилиндрическом колесе прочность зуба определяется его формой и размерами в нормальном сечении. Форма зуба в нормальном сечении n-n (рис. 7.8) соответствует форме зуба условного прямозубого колеса с модулем mn и диаметром dv=2rv, где rv – радиус кривизны эллипса в точке Р.
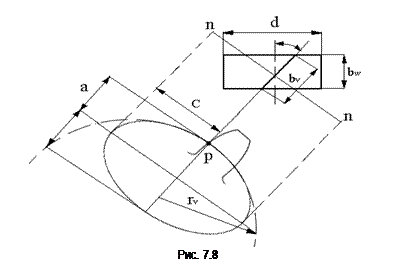 Размеры полуосей эллипса определяются в виде
Размеры полуосей эллипса определяются в виде 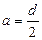 и
и 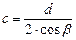 .
.
Известно, что для эллипса 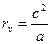 , тогда диаметр эквивалентного колеса
, тогда диаметр эквивалентного колеса
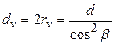 .
.
С другой стороны диаметр эквивалентного колеса можно выразить как 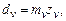
где 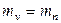 ;
; 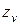 - эквивалентное число зубьев.
- эквивалентное число зубьев.
Так как 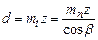 , то
, то 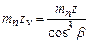 , откуда
, откуда 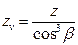 .
.
Если принять ширину колеса 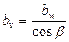 , то такое колесо будет равнопрочным косозубому и называется эквивалентным колесом.
, то такое колесо будет равнопрочным косозубому и называется эквивалентным колесом.
Дата добавления: 2017-03-12; просмотров: 1781;











