Проектировочный расчет. Для проектировочного расчета представим ширину зубчатого венца в виде

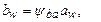(6.6)

где 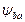-коэффициент ширины зубчатого венца относительно межосевого расстояния .

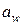Начальный диаметр шестерни выразим через передаточное отношение U и межосевое расстояние

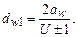(6.7)

Подставив выражения (6.6) и (6.7) в уравнение (6.5) и возведя обе части в квадрат, получим

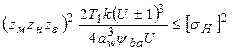
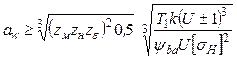откуда

или

,

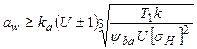где 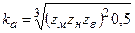- вспомогательный коэффициент.

Для зубчатых передач низкой точности среднее значение этого коэффициента определяется по таблицам или графикам, приводимым в справочниках.

Расчет на изгибную прочность

Расчет зубьев на изгиб производится в предположении:

1. Вся нагрузка зацепления передается одной парой зубьев и приложена к вершине зуба, что возможно в том случае, если их деформации 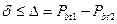(разность основных шагов);

2. Зуб рассматривается как консольная балка, для которой справедливы методы сопротивления материалов;

3. Силами трения пренебрегаем.

Под нагрузкой зуб деформируется (рис 6.2), тогда угол .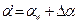

Рассмотрим отдельно один зуб шестерни (рис.6.3).

Перенесём силу F_n вдоль линии зацепления, что возможно, ибо это окажет действие только на участке переноса, но никак не в опасном сечении по изгибу. Опасным будет сечение а-а' там, где балка равнопрочного сечения, имеющая вид параболы, пересекается с поверхностью зуба. Сила F_t' изгибает, а F_r' сжимает зуб. Согласно эпюре (рис. 6.3) напряжение в наиболее опасной точке a

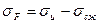. (6.8)

Изгибающие напряжения

,

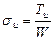где T_и – изгибающий момент;W– момент сопротивления изгибу в опасном сечении.

Размеры опасного сечения S₀ и b_w,а расстояние от точки приложения усилия до опасного расчетного сечения l₀.

Принимая 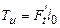и 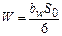, получим

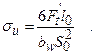(6.9)

Напряжения сжатия определяются в виде

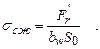(6.10)

Подставив выражения (6.9) и (6.10) в равенство (6.8), с учетом концентрации напряжений у ножки зуба (учитывается коэффициентом k_s ), получим

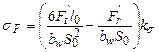, (6.11).

где 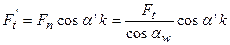; (6.12)

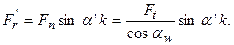(6.13)

В опасном сечение принимаем S₀=S’ 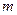и 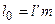, где S’ и l’– безразмерные коэффициенты.

Подставив выражения (6.12) и (6.13) в уравнение (6.11), получим

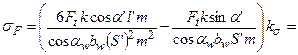
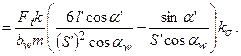
Обозначим 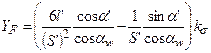- коэффициент формы зуба. Это безразмерный коэффициент, величина которого зависит только от формы зуба (l’, S’, a’), в том числе и от формы галтели (k_s). Ранее было показано, что форма зуба при одинаковом исходном контуре инструмента зависит в основном от числа зубьев колеса z и коэффициента смещения инструмента x,таким образом, Y_F=f(z, x, a).

Для колес с внутренним зацеплением

.

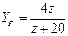Условие прочности по изгибу будет

.

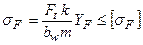Учитывая, что 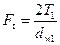, получим формулу для проверочного расчета

. (6.14)

Так как число зубьев шестерни и колеса различно, то различны Y_F1 и Y_F2, поэтому проверочный расчет для шестерни и колеса нужно делать отдельно.

Проектировочный расчет на изгиб. Возможны два варианта решения.

1. Рассмотрим случай, когда из расчета по контактным напряжениям известны a_w и b_w. Из формулы (6.14) выражаем 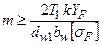, учитывая,

что 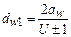, окончательно получаем выражение для модуля

.

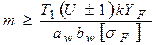2. Если габариты передачи определяются изгибной прочностью и известно z₁, то для некорригированной передачи d_w1=d₁=mz₁.

Обозначим 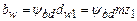, тогда

.

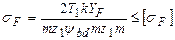Откуда получаем выражение для определения модуля при проектировочном расчете

.

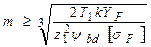Лекция №7

Передача цилиндрическими колесами с косыми зубьями.