Локальный алгоритм А.
Рассмотрим задачу Z ЦЛП с бинарными переменными :
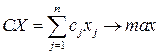 (8.1)
(8.1)
при ограничениях
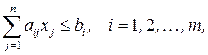 (8.2)
(8.2)
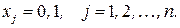 (8.3)
(8.3)
Определение 8.1. Множество 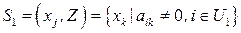 называется окрестностью первого порядка переменной
называется окрестностью первого порядка переменной 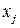 , здесь
, здесь 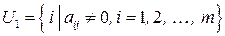 .
.
Введем понятия 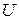 -окрестности и
-окрестности и 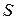 -окрестности:
-окрестности:
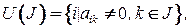
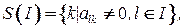
где 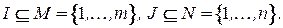
Окрестность произвольного порядка переменной 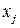 определяется по индукции. Пусть известна окрестность
определяется по индукции. Пусть известна окрестность 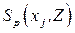 р-го порядка. Окрестность
р-го порядка. Окрестность 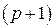 -го порядка определим так:
-го порядка определим так: 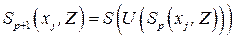 .
.
Замечание. Введенное выше, в параграфе 8.1, понятие окрестности 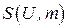 является весьма общим и пригодно для построения локальных алгоритмов вычисления информации в задачах дискретной математики общего вида, понятие окрестности переменной
является весьма общим и пригодно для построения локальных алгоритмов вычисления информации в задачах дискретной математики общего вида, понятие окрестности переменной 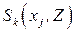 , используемое в локальном алгоритме декомпозиции задач ДО, является частным случаем окрестности
, используемое в локальном алгоритме декомпозиции задач ДО, является частным случаем окрестности 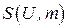 , причем окрестность переменной является изоморфной вершинной окрестности вершины графа, это становится понятным, если рассмотреть графовую интерпретацию системы ограничений задачи ДО, при которой каждой переменной
, причем окрестность переменной является изоморфной вершинной окрестности вершины графа, это становится понятным, если рассмотреть графовую интерпретацию системы ограничений задачи ДО, при которой каждой переменной 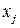 задачи ДО ставится в соответствие вершина
задачи ДО ставится в соответствие вершина 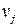 графа
графа 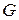 , причем две вершины
, причем две вершины 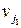 и
и 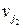 соединяются ребром
соединяются ребром 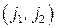 , если существует хотя бы одно ограничение задачи ДО, в которое входят обе переменные
, если существует хотя бы одно ограничение задачи ДО, в которое входят обе переменные 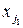 и
и 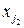 , при данной интерпретации окрестности вершин графа
, при данной интерпретации окрестности вершин графа 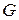 взаимно однозначно соответствуют окрестностям переменных задачи ДО.
взаимно однозначно соответствуют окрестностям переменных задачи ДО.
Введем так называемое внешнее кольцо 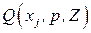 , т.е. следующее множество переменных:
, т.е. следующее множество переменных: 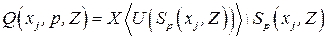 .
.
Опишем ЛА 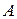 .
.
1. Выберем некоторую переменную 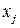 задачи
задачи 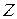 .
.
2. Построим окрестность 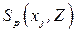 и множество
и множество 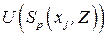 .
.
3. Определим внешнее кольцо: 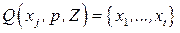 .
.
4. Рассмотрим задачу 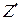 , переменные которой составляют окрестность
, переменные которой составляют окрестность 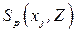 , с ограничениями с индексами
, с ограничениями с индексами 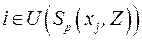 , целевая функция получается из исходной целевой функции задачи
, целевая функция получается из исходной целевой функции задачи 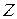 удалением переменных
удалением переменных 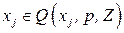 , а значения переменных
, а значения переменных 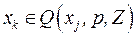 фиксированы.
фиксированы.
5. Решим задачу 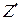 для всевозможных булевых наборов
для всевозможных булевых наборов 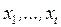 (всего их
(всего их 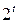 ).
).
6. Если в результате решения этих задач получим, что либо
а) 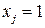 во всех оптимальных решениях задач
во всех оптимальных решениях задач 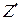 , либо
, либо
б) 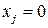 во всех оптимальных решениях задач
во всех оптимальных решениях задач 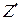 ,
,
тo в случае а) 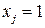 в оптимальном решении исходной задачи
в оптимальном решении исходной задачи 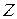 , а в случае б)
, а в случае б) 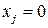 в оптимальном решении исходной задачи
в оптимальном решении исходной задачи 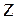 .
.
7. Если в п. 6 имел место случай а) или б), переменной присваивается соответствующее значение и она исключается из задачи 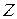 .
.
8. Перейти к п.1.
Как следует из вышеизложенного, в ЛА каждой переменной ставится в соответствие информационный вектор 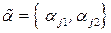 , содержащий информацию о предикатах
, содержащий информацию о предикатах 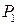 : «
: « 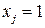 во всех оптимальных решениях задачи
во всех оптимальных решениях задачи 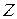 » и
» и 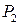 : «
: « 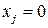 во всех оптимальных решениях задачи
во всех оптимальных решениях задачи 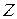 ». Если
». Если 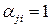 , то
, то 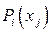 ‑ истинный; если же
‑ истинный; если же 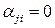 , то
, то 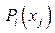 ‑ ложный; если
‑ ложный; если 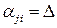 , то информация об истинности предиката
, то информация об истинности предиката 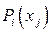 отсутствует. Таким образом, ЛА
отсутствует. Таким образом, ЛА 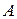 позволяет переходить от одного множества переменных
позволяет переходить от одного множества переменных 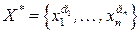 к другому множеству
к другому множеству 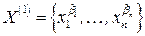 , содержащему больше информации о решении задачи
, содержащему больше информации о решении задачи 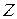 ,т.е.
,т.е.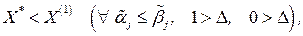 причем
причем 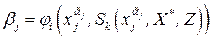 ,
, 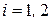 , где
, где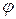 ‑функция ЛА.
‑функция ЛА.
8.2.3. Локальный декомпозиционный алгоритм 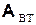 решения задач дискретной оптимизации с блочно-древовидной структурой
решения задач дискретной оптимизации с блочно-древовидной структурой
В настоящем разделе рассматривается ЛА 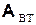 решения блочно-древовидных задач ДО, т.е. задач, в которых возможно выделить систему окрестностей различных переменных такую, что одна переменная может быть обшей самое большее лишь для двух окрестностей и граф пересечений этих окрестностей представляет собой дерево. С помощью ЛА
решения блочно-древовидных задач ДО, т.е. задач, в которых возможно выделить систему окрестностей различных переменных такую, что одна переменная может быть обшей самое большее лишь для двух окрестностей и граф пересечений этих окрестностей представляет собой дерево. С помощью ЛА 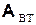 можно решить подобнуюзадачу ДО, двигаясь от окрестностей, соответствующих листьям дерева, к окрестности, соответствующей корню дерева.
можно решить подобнуюзадачу ДО, двигаясь от окрестностей, соответствующих листьям дерева, к окрестности, соответствующей корню дерева.
Введем необходимые для дальнейшего изложения понятия. Пусть 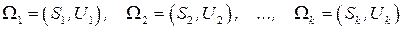 ‑ система окрестностей некоторых переменных
‑ система окрестностей некоторых переменных 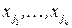 , где
, где 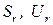 ‑ соответственно множества индексов переменных и ограничений для
‑ соответственно множества индексов переменных и ограничений для 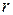 -й окрестности,
-й окрестности, 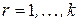 , причем
, причем
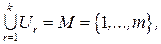 (8.4)
(8.4)
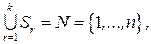 (8.5)
(8.5)
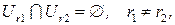 (8.6)
(8.6)
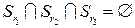 (8.7)
(8.7)
для любой тройки индексов 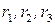 .
.
Замечание. Отметим, что при определении понятия блочно-древовидной структуры мы пользуемся понятием окрестности, а не блока, хотя эти два понятия тесно связаны. Дело в том, что блочную структуру в матрице инциденций задачи ДО можно выделить с помощью анализа окрестностей переменных, нетрудно видеть, что если путем перестановки строк и столбцов матрицы инциденций и переменных и ограничений (8.2) задачи ДО (8.1)‑(8.3) можно собрать вместе ограничения с индексами из 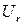 и переменные с индексами из
и переменные с индексами из 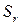 , то мы получим подматрицу – блок.
, то мы получим подматрицу – блок.
Нетрудно видеть, что блочно-древовидная структура является частным случаем древовидной декомпозиции.
Введем понятие графа инцидентности (или графа пересечений) 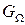 окрестностей
окрестностей 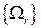 аналогично понятию графа пересечений
аналогично понятию графа пересечений 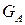 булевой матрицы
булевой матрицы 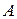 . Граф пересечений окрестностей
. Граф пересечений окрестностей 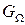 имеет вершины
имеет вершины 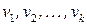 , соответствующие выделенным окрестностям
, соответствующие выделенным окрестностям 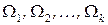 , причем две вершины графа
, причем две вершины графа 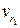 и
и 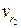 , отвечающие окрестностям
, отвечающие окрестностям 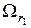 и
и 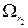 , соединены ребром
, соединены ребром 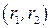 , если
, если 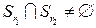 .
.
Определение 8.2.Блочно-древовидной назовем задачу ДО, для которой можно выделить систему окрестностей 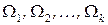 , удовлетворяющую свойствам (8.4) ‑ (8.7), причем граф пересечений окрестностей
, удовлетворяющую свойствам (8.4) ‑ (8.7), причем граф пересечений окрестностей 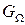 является деревом.
является деревом.
Будем говорить, что описанная задача ДО имеет блочно-древовидную (БД) структуру.
Замечание. Частным случаем БД структуры является квазиблочная структура, для которой граф пересечений окрестностей (или блоков) является линейным деревом (путем) (рис. 8.1).
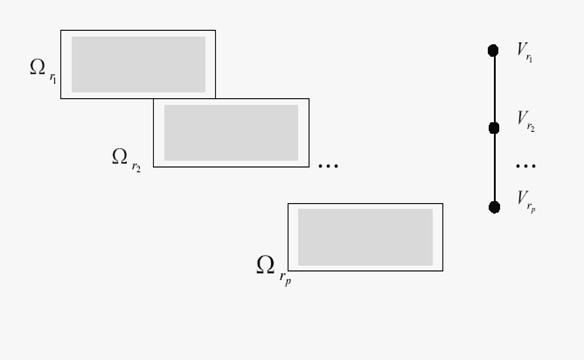
Рис 8.1. Квазиблочная структура.
Одним из первых классов больших разреженных задач линейного программирования, которые начал изучать создатель линейного программирования G. Dantzig, был класс квазиблочных (или «лестничных») задач ЛП для динамического планирования[2]. Имеются другие примеры квазиблочных задач ЛП для многоэтапного планирования, составления расписаний, назначений и многоэтапного структурного проектирования. Квазиблочную структуру имеют задачи оптимального резервирования гостиничных номеров[3], аналогичные последним темпоральные задачи о ранце[4], получившие в последнее время применение при решении задач предварительного резервирования вычислительных ресурсов в Grid Computing, задачи линейного динамического программирования[5], некоторые задачи управления трудовыми ресурсами, динамические модели экономики, учитывающие в явном виде фактор времени, задачи управления в иерархических (обычно древовидных)структурах, сетевые задачи.
Для решения квазиблочных задач ДО достаточно эффективен локальный алгоритм декомпозиции, использующий специфику квазиблочной матрицы ограничений. Локальный алгоритм (ЛА) имеет декомпозиционный характер, т.е. сводит решение исходной задачи ДО большой размерности к решению ряда задач меньших размерностей, которые уже можно решить известными методами, т.е. с помощью имеющихся решателей.
Изложим ЛА 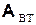 решенияБД задач ЦЛП вида (8.1) ‑(8.3),где матрица
решенияБД задач ЦЛП вида (8.1) ‑(8.3),где матрица 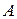 имеет БД структуру, содержащую
имеет БД структуру, содержащую 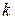 блоков, и этой структуре соответствует дерево
блоков, и этой структуре соответствует дерево 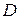 инцидентности блоков.
инцидентности блоков.
Рассмотрим вершину 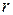 дерева
дерева 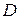 и дерево Dr, состоящее из вершины
и дерево Dr, состоящее из вершины 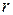 и всех ее потомков. Введем необходимые обозначения:
и всех ее потомков. Введем необходимые обозначения: 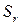 ‑ множество индексов переменных, принадлежащих блоку
‑ множество индексов переменных, принадлежащих блоку 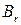 ;
; 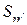 ‑ множество индексов переменных, принадлежащих одновременно блокам
‑ множество индексов переменных, принадлежащих одновременно блокам 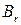 и
и 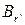 ; если
; если 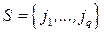 , то
, то 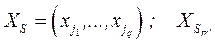 ‑ вектор переменных, общих для блоков
‑ вектор переменных, общих для блоков 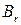 и
и 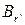 .
.
Обозначим через 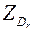 следующую задачу: для каждого вектора
следующую задачу: для каждого вектора 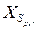 найти
найти 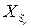 и
и 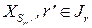 , такие, чтобы
, такие, чтобы
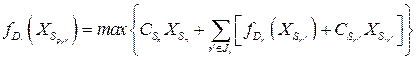
при ограничениях
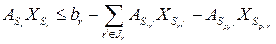 ,
,
здесь 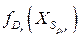 ‑ значение целевой функции задачи
‑ значение целевой функции задачи 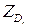 , соответствующей дереву
, соответствующей дереву 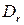 .
.
Решение задачи 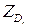 для вершины
для вершины 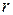 графа
графа 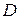 при фиксированном векторе
при фиксированном векторе 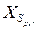 обозначим таким образом:
обозначим таким образом:
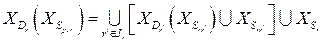 .
.
Понятно, что 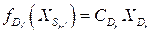 .
.
Нетрудно заметить, что если зафиксировать вектор 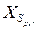 , то задача (8.1)‑(8.3) распадается на две задачи: первая соответствует дереву
, то задача (8.1)‑(8.3) распадается на две задачи: первая соответствует дереву 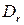 ; а вторая –
; а вторая – 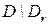 . На этом свойстве и основано применение ЛА
. На этом свойстве и основано применение ЛА 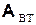 для решения БД задач ДО.
для решения БД задач ДО.
Алгоритм 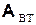 вычисляет информацию, поднимаясь от листьев дерева к корневой вершине. Изложим ЛА
вычисляет информацию, поднимаясь от листьев дерева к корневой вершине. Изложим ЛА 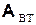 решения БД задачи ДО, характеризующейся деревом
решения БД задачи ДО, характеризующейся деревом 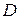 инцидентности блоков с
инцидентности блоков с 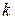 вершинами, состоящим из
вершинами, состоящим из 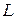 слоев. Пусть в
слоев. Пусть в 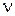 -м слое имеется
-м слое имеется 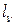 вершин
вершин 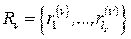 , разбитых на подмножества
, разбитых на подмножества 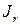 .
.
Алгоритм
Шаг 1. Положить 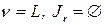 для всех
для всех 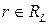 .
.
Шаг 2. Для каждой вершины 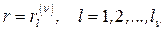 слоя
слоя 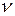 дерева
дерева 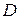 решить задачу
решить задачу 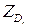 . Если эта задача не имеет решения ни для одной вершины данного слоя ‑ перейти к шагу 5, в противном случае ‑ к шагу 3.
. Если эта задача не имеет решения ни для одной вершины данного слоя ‑ перейти к шагу 5, в противном случае ‑ к шагу 3.
Шаг 3. Если 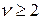 , то перейти на слой выше, т.е. положить
, то перейти на слой выше, т.е. положить 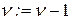 и перейти к шагу 2, иначе ‑ к шагу 4.
и перейти к шагу 2, иначе ‑ к шагу 4.
Шаг 4.Конец вычислений. Решение задачи 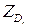 на уровне
на уровне 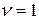 является решением исходной задачи:
является решением исходной задачи: 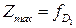 .
.
Шаг 5. Конец вычислений. Задача не имеет допустимых решений.
Пример, иллюстрирующий работу алгоритма 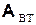 . Решим имеющую БД структуру задачу ЦЛП, которой соответствует дерево инцидентности блоков на рис.8.2:
. Решим имеющую БД структуру задачу ЦЛП, которой соответствует дерево инцидентности блоков на рис.8.2:
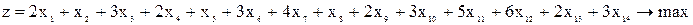 при ограничениях:
при ограничениях:
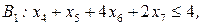
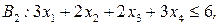
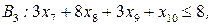
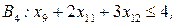
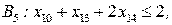
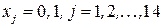 .
.
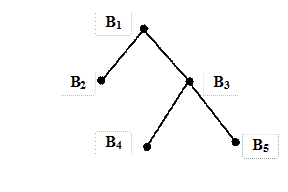
Рис. 8.2. Дерево инцидентности блоков в примере.
Начнем решение со слоя 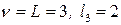 . Рассмотрим задачу, соответствующую
. Рассмотрим задачу, соответствующую 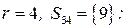
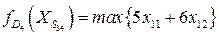
при ограничениях 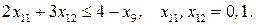
Если 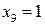 , то
, то 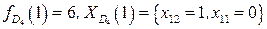 . Если
. Если 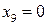 , то
, то 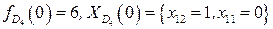 .
.
Для 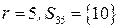 соответствующая задача имеет вид
соответствующая задача имеет вид
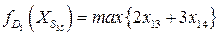
при ограничениях 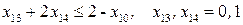 .
.
Если 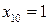 , то
, то 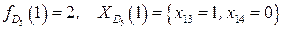 . Если
. Если 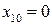 , то
, то 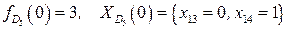 .
.
Таким образом, все вершины слоя 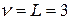 рассмотрены.
рассмотрены.
Перейдем на слой 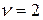 . Рассмотрим вершину
. Рассмотрим вершину 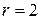 . Для нее
. Для нее 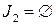 , вершина-предок
, вершина-предок 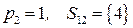 . Соответствующая задача имеет вид
. Соответствующая задача имеет вид 
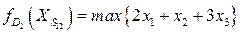
при ограничениях 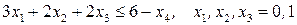 .
.
Если 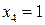 , то
, то 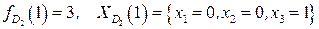 .
.
Если 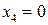 , то
, то 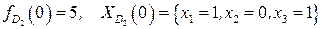 .
.
Рассмотрим вершину 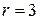 . Для нее
. Для нее 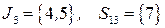 . Нужно решить задачу
. Нужно решить задачу
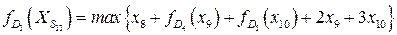
при ограничениях 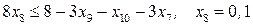 .
.
Если 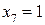 , то
, то 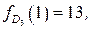
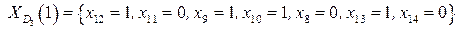 ,
,
если 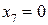 , то
, то 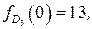
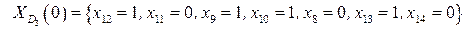 .
.
Все задачи слоя 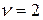 рассмотрены.
рассмотрены.
Перейдем к слою 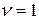 , здесь всего одна вершина
, здесь всего одна вершина 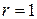 , причем
, причем 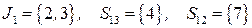 . Соответствующая задача
. Соответствующая задача 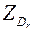 имеет вид
имеет вид 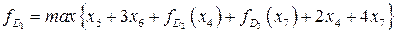
при ограничениях 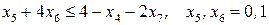 .
.
Решаем эту задачу, получаем, что оптимальному решению соответствуют 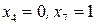 , причем
, причем 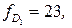
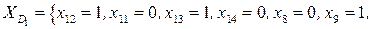
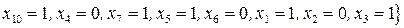 .
.
Упорядочивая переменные, приходим к тому, что решение исходной задачи (которое, как уже отмечено, совпадает с решением задачи 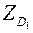 ) имеет вид x1=1, x2=0, x3=1, x4=0, x5=1, x6=0, x7=1, x8=0, x9=1, x10=1, x11=0, x12=1, x13=1, x14=0, Zmax=23.
) имеет вид x1=1, x2=0, x3=1, x4=0, x5=1, x6=0, x7=1, x8=0, x9=1, x10=1, x11=0, x12=1, x13=1, x14=0, Zmax=23.
Дата добавления: 2016-06-05; просмотров: 1489;











