Несериальное динамическое программирование и локальные элиминационные алгоритмы для разреженных задач дискретной оптимизации.

При изучении сложных объектов не всегда возможно получить (или вычислить) полную информацию об объекте в целом, поэтому представляет интерес получение информации об объекте, рассматривая его по частям, т.е. локально, производя локальные вычисления.

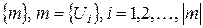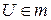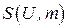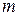Ю.И. Журавлев [7] ввел и исследовал локальные алгоритмы вычисления информации. Локальный алгоритм задается следующим образом. Для заданной системы множеств и для каждого элемента определим окрестность в , причем окрестности должны удовлетворять следующим условиям:

1) 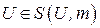; 2) 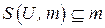; 3) Если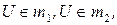 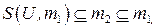то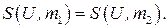

Если на паре 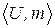определены окрестности 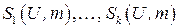, говорят, что на множестве 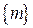введена система окрестностей.

Приведенное определение окрестности является весьма общим. В качестве конкретного примера может служить понятие окрестности вершины графа. Ниже, в разделе 8.2 приведены примеры окрестностей переменной в задаче дискретной оптимизации.

Если для некоторого 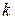выполнено условие 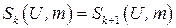для всех пар 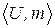, тo система окрестностей 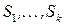называется конечной.

Будем считать, что на парах 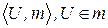определена система двухместных предикатов 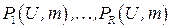, которая разбита на два непересекающихся под­мно­жества 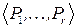, 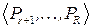. Элементы первого подмножества называются основными предикатами, а элементы второго – вспомогательными.

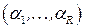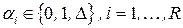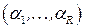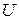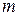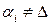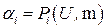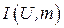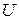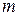Вектор называется информационным, если . Вектор называется допустимым для в , если для всех выполнено соотношение , информационной системой называется множество всех допустимых для в информационных векторов.

Пусть 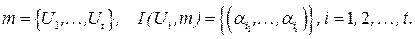Множество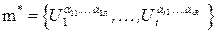называется допустимым для 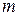; класс 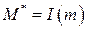всех допустимых для 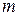множеств 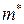называется информационным классом множества 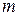по системе предикатов .

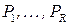Понятно, что окрестность 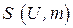определяет окрестность 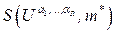. Введем систему функций 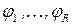, порождающих алгоритм:

.

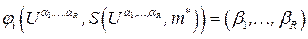Функции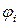определены на всех парах 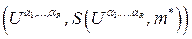,таких, что 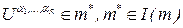и удовлетворяют следующим условиям:

1) 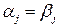, если ;

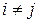2) множество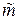 ,которое получается из 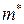заменой элемент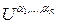а на 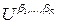, допустимодля .

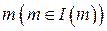Пары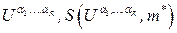обозначим 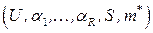.Введем отношение частичного порядка:

1. Если 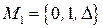, то.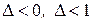

2. Пусть 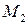‑ множество информационных векторов длины 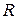:тогда 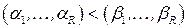.если .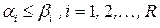

3. для множеств элементов с отметкам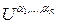и и 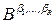полагаем 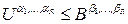, есл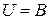и и .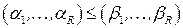

4. для множества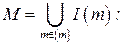 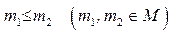, если

а) 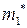и 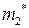принадлежат одному информационному классу 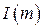и

б) если , ,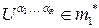

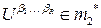то .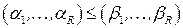

5. Для множества окрестностей :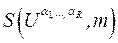

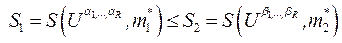, если 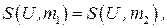а из условий 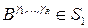, , 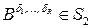следует ,что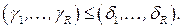

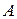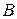Пусть и – элементы одного из множеств, перечисленных выше в п.п. 1-5. Есл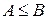и и 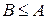, то элементы 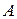и 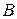назовем равными по информации и обозначим это так: .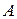

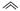
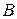Функцию 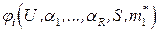назовем монотонной, если из соотношения 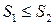следует, что .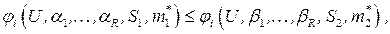

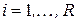Для определения локального алгоритма введем также алгоритм упорядочения 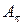и 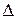‑ оператор по системе предикатов. Пусть 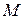– произвольное множество, составленное из элементов с информационными векторами; 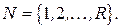Рассмотрим множество 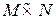всех пар 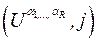таких, что 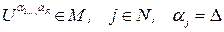, алгоритм 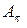упорядочивает множество 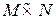. 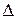‑ оператор по системе 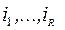над 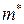, который заменяет в информационных векторах всех элементов из 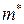значения всех координат, кроме координат с номерами 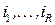, на 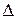, обозначим этот оператор 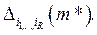Алгоритм 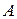полностью определяется системой предикатов 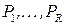, разбиением этой системы на основные 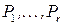и вспомогательные 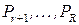предикаты, системой монотонных функций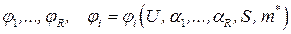и алгоритмом 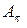. Пусть .

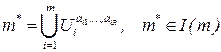Опишем первый шаг локального алгоритма 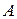. К множеству 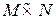( 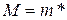, 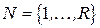) применим алгоритм 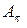, выделим первую по порядку пару 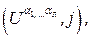вычислим функцию 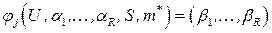, элемент 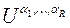заменяем на 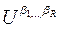, если 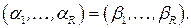Берем вторую по порядку пару и т.д., если для всех элементов 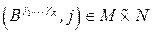выполнено ра­венство 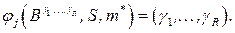Алгоритм 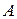заканчивает свою работу пос­ле просмотра всех пар из 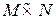, в противном случае найдется первая по порядку пара 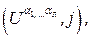для которой 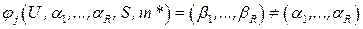. Элемент 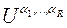заменяем на 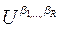. Множество 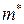переходит в 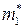. Производится проверка: остались ли в 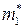элементы, у которых на первых r местах в информационных векторах имеется хотя бы один символ 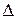, если таких элементов нет, алгоритм 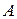заканчивает работу; если они есть ‑ заканчивается первый шаг локального алгоритма .

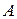Пусть выполнено 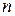шагов локального алгоритма 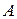, описание 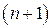-го шага алгоритма в точности повторяет описание первого шага, если вместо множества 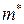рассматривать множество 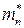, в которое перешло 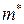после 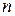шагов алгоритма 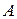. В силу монотонности функции 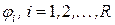, алгоритм 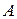заканчивает работу после конечного числа шагов.

Таким образом, локальный алгоритм характеризуется двумя параметрами: величиной окрестности, изучаемой на каждом шаге работы алгоритма, и числом признаков, запоминающихся о каждом элементе изучаемого множества (последний параметр называют еще памятью локального алгоритма). Основными теоремами теории локальных алгоритмов вычисления информации являются теорема единственности и теорема существования наилучшего (или мажорантного) локального алгоритма, первая теорема утверждает, что результат вычисления основных предикатов локального алгоритма с монотонными функциями не зависит от алгоритма 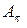(т.е. от порядка рассмотрения элементов множества 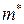). Вторая теорема доказывает существование для всякого класса локально равных алгоритмов с одинаковой памятью мажорантного локального алгоритма, т.е. алгоритма, который по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой алгоритм из рассматриваемого класса. Отметим, что доказательство этой теоремы имеет неконструктивный характер, т.е. не позволяет осуществить прямое построение эффективного наилучшего алгоритма. Построение мажорантного локального алгорит­ма в явной форме реализовано лишь в отдельных случаях: для задачи построения минимального покрытия множества 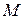системой множеств 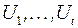; для задач вы­числения информации о том, входит или не входит ребро графа в какой-либо тупи­ковый путь между двумя полюсами; построены также мажорантные локальные алгоритмы минимизации дизъюнктивных нормальных форм алгебры логики.