Алгоритм Боуера и Мура

Алгоритм Бойера-Мура, разработанный двумя учеными - Бойером (Robert S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке. Прежде чем рассмотреть работу этого алгоритма, уточним некоторые термины. Под строкой мы будем понимать всю последовательность символов текста. Собственно говоря, речь не обязательно должна идти именно о тексте. В общем случае строка - это любая последовательность байтов. Поиск подстроки в строке осуществляется по заданному образцу, т. е. некоторой последовательности байтов, длина которой не превышает длину строки. Наша задача заключается в том, чтобы определить, содержит ли строка заданный образец.

Главное отличие алгоритма Бойера-Мура от алгоритма грубой силы заключается в том, что мы начинаем проверку совпадения образца и фрагмента строки не с первого, а с последнего символа образца. Таким образом, если в образце последний символ не совпадает с соответствующим символом строки, мы можем выполнить смещение образца относительно строки более чем на один символ (часто - на всю длину образца).

Простейший вариант алгоритма Бойера-Мура состоит из следующих шагов. На первом шаге мы строим таблицу смещений для искомого образца. Процесс построения таблицы будет описан ниже. Далее мы совмещаем начало строки и образца и начинаем проверку с последнего символа образца. Если последний символ образца и соответствующий ему при наложении символ строки не совпадают, образец сдвигается относительно строки на величину, полученную из таблицы смещений, и снова проводится сравнение начиная с последнего символа образца. Если же символы совпадают, производится сравнение предпоследнего символа образца и т. д. Если все символы образца совпали с наложенными символами строки, значит мы нашли подстроку и поиск окончен. Если же какой-то (не последний) символ образца не совпадает с соответствующим символом строки, мы сдвигаем образец на один символ вправо и снова начинаем проверку с последнего символа. Весь алгоритм выполняется до тех пор, пока либо не будет найдено вхождение искомого образца, либо не будет достигнут конец строки.

Величина сдвига в случае несовпадения последнего символа вычисляется исходя из следующих соображений: сдвиг образца должен быть минимальным, таким, чтобы не пропустить вхождение образца в строке. Если данный символ строки встречается в образце, мы смещаем образец таким образом, чтобы символ строки совпал с самым правым вхождением этого символа в образце. Если же образец вообще не содержит этого символа, мы сдвигаем образец на величину, равную его длине, так что первый символ образца накладывается на следующий за проверявшимся символ строки.

Величина смещения для каждого символа образца зависит только от порядка символов в образце, поэтому смещения удобно вычислить заранее и хранить в виде одномерного массива, где каждому символу алфавита соответствует смещение относительно последнего символа образца. Поясним все вышесказанное на простом примере. Пусть у нас есть алфавит из пяти символов: a, b, c, d, e и мы хотим найти вхождение образца "abbad" в строке "cbeccacbadbabbad". Следующие схемы иллюстрируют все этапы выполнения алгоритма:

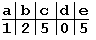
Таблица смещений для образца "abbad".

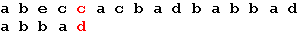
Начало поиска. Последний символ образца не совпадает с наложенным символом строки. Сдвигаем образец вправо на 5 позиций:

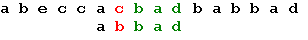
Три символа образца совпали, а четвертый - нет. Сдвигаем образец вправо на одну позицию:

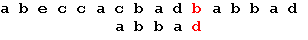
Последний символ снова не совпадает с символом строки. В соответствии с таблицей смещений сдвигаем образец на 2 позиции:

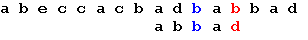
Еще раз сдвигаем образец на 2 позиции:

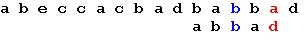
Теперь, в соответствии с таблицей, сдвигаем образец на одну позицию, и получаем искомое вхождение образца:

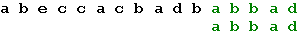
Подстроку в строке совпала.

ЛЕКЦИЯ 21. МЕТОДЫ ПОИСКА ВО ВНЕШНЕЙ ПАМЯТИ.ФАЙЛОВЫЕ СТРУКТУРЫ ДАННЫХ

Цели и задачи лекции:Ознакомиться с файловыми структурами данных.

Основные вопросы: классификация файлов, файлы с плотным и неплотным индексом, хэширование.

Файлы и файловые структуры, которые используются для хранения информации во внешней памяти, можно классифицировать следующим образом:

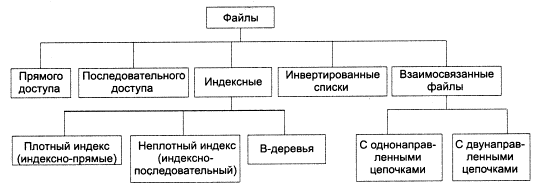
Файл – поименованная область памяти на внешнем носителе. С точки зрения пользователя, файл - линейная последовательность записей, расположенных на внешних носителях.

На устройствах с последовательным доступом вся память рассматривается как линейная последовательность информационных элементов.

Файлы с постоянной длиной записи, расположенные на устройствах прямого доступа, являются файлами прямого доступа. В этих файлах физический адрес расположения нужной записи может быть вычислен по номеру записи (NZ).

Прямой доступ к данным. Для файлов с постоянной длиной записи адрес размещения записи с номером К может быть вычислен по формуле:
ВА+ (К- 1) * LZ + 1, где ВА - базовый адрес, LZ - длина записи.
Файлы прямого доступа обеспечивают наиболее быстрый доступ к произвольным записям.

На устройствах последовательного доступа могут быть организованы файлы только последовательного доступа. Файлы с переменной длиной записи всегда являются файлами последовательного доступа. Они могут быть организованы двумя способами:

1.Конец записи отличается специальным маркером.

Запись1 ХХ Запись2 ХХ Запись3 ХХ

2.В начале каждой записи записывается ее длина (LZ).

LZ1Запись1LZ2Запись2LZ3Запись3… LZN ЗаписьN.

Хеширование данных

Метод хэширования для таблиц данных мы уже рассматривали. Коротко рассмотрим его применимость при работе с файлами. Суть методов хеширования состоит в том, что мы берем значения ключа (или некоторые его характеристики) и используем его для начала поиска, то есть мы вычисляем некоторую хеш-функцию h(k) и полученное значение берем в качестве адреса начала поиска. То есть не требуется полного взаимно-однозначного соответствия, но, с другой стороны, для повышения скорости мы ограничиваем время этого поиска (количество дополнительных шагов) для окончательного получения адреса. Таким образом, мы допускаем, что нескольким разным ключам может соответствовать одно значение хеш-функции (один адрес). Подобные ситуации называются коллизиями. Значения ключей, которые имеют одно и то же значение хеш-функции, называются синонимами. Поэтому при использовании хеширования как метода доступа необходимо принять два независимых решения: выбрать хэш-функцию; выбрать метод разрешения коллизий.

Стратегия разрешения коллизий с областью переполнения
Первая стратегия условно может быть названа стратегией с областью переполнения. При выборе этой стратегии область хранения разбивается на 2 части: основную область; область переполнения.

Для каждой новой записи вычисляется значение хэш-функции, которое определяет адрес ее расположения, и запись заносится в основную область в соответствии с полученным значением хэш-функции.
Если вновь заносимая запись имеет значение функции хеширования такое же, которое использовала другая запись, уже имеющаяся в БД, то новая запись заносится в область переполнения на первое свободное место, а в записи-синониме, которая находится в основной области, делается ссылка на адрес вновь размещенной записи в области переполнения. Если же уже существует ссылка в записи-синониме, которая расположена в основной области, то тогда новая запись получает дополнительную информацию в виде ссылки и уже в таком виде заносится в область переполнения. При этом цепочка синонимов не разрывается, но мы не просматриваем ее до конца, чтобы расположить новую запись в конце цепочки синонимов, а располагаем всегда новую запись на второе место в цепочке синонимов, что существенно сокращает время размещения новой записи. При таком алгоритме время размещения любой новой записи составляет не более двух обращений к диску, с учетом того, что номер первой свободной записи в области переполнения хранится в виде системной переменной.

Рассмотрим механизмы поиска произвольной записи и удаления записи для этой стратегии хеширования. При поиске записи также сначала вычисляется значение ее хэш-функции и считывается первая запись в цепочке синонимов, которая расположена в основной области. Если искомая запись не соответствует первой в цепочке синонимов, то далее поиск происходит перемещением по цепочке синонимов, пока не будет обнаружена требуемая запись. Скорость поиска зависит от длины цепочки синонимов, поэтому качество хэш-функции определяется максимальной длиной цепочки синонимов. Хорошим результатом может считаться наличие не более 10 синонимов в цепочке.
При удалении произвольной записи сначала определяется ее место расположения. Если удаляемой является первая запись в цепочке синонимов, то после удаления на ее место в основной области заносится вторая (следующая) запись в цепочке синонимов, при этом все указатели (ссылки на синонимы) сохраняются.

Если же удаляемая запись находится в середине цепочки синонимов, то необходимо провести корректировку указателей: в записи, предшествующей удаляемой, в цепочке ставится указатель из удаляемой записи. Если это последняя запись в цепочке, то все равно механизм изменения указателей такой же, то есть в предшествующую запись заносится признак отсутствия следующей записи в цепочке, который ранее хранился в последней записи.