Дифференциальное уравнение теплопроводности

При решении задач, связанных с теплопроводностью тел, необходимо определить температурное поле, т.е. характер изменения температуры в исследуемой области. Это может быть сделано с помощью дифференциального уравнения теплопроводности.

Вывод этого уравнения сделаем при следующих упрощающих задачу предположениях:

1) рассматриваемое тело однородно, а его физические свойства (плотность 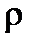, удельная теплоёмкость c и коэффициент теплопроводности 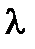) не зависят от температуры;

2) внутренние источники теплоты отсутствуют.

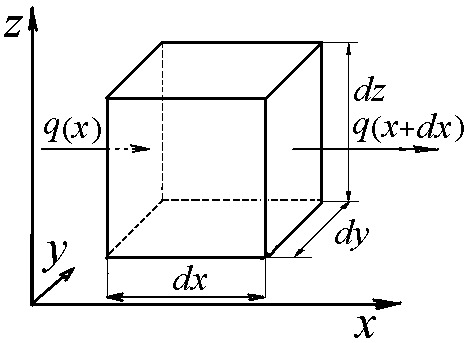
Рис. 1.2

Сначала рассмотрим тело, температурное поле в котором одномерное, т.е. температура изменяется только в одном направлении, например, вдоль координаты x (рис. 1.2).

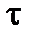Выделим в рассматриваемом теле элементарный параллелепипед, объём которого равен dxdydz, а грани, нормальные к оси x, являются изотермическими поверхностями. За некоторое время в этот параллелепипед поступает количество теплоты, равное q(x)dydzd , а выходит теплота в количестве, равном q(x+dx)dydzd 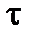. В результате за это же время температура выделенного параллелепипеда (массой dM = изменится на dT. В соответствии с законом сохранения энергии получим

,

где полная производная 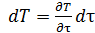, a ,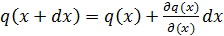

тогда .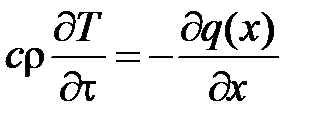

Частные производные в этой формуле подчёркивают, что как Т, так и q могут зависеть и от 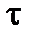, и от x.

Кроме того, по закону Фурье в данном случае q(x) 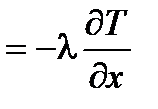. Подставляя это значение q(x) в последнее уравнение, получим дифференциальное уравнение теплопроводности для нестационарногоодномерноготемпературного поля: c 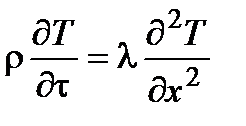, или ,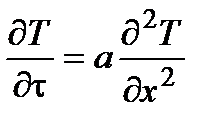

где величина a = 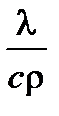(с единицей измерения м 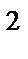/с) называется коэффициентом температуропроводности.

Соответственно дифференциальное уравнение теплопроводности дляслучая нестационарноготрёхмерноготемпературного поля будет иметь вид:

.

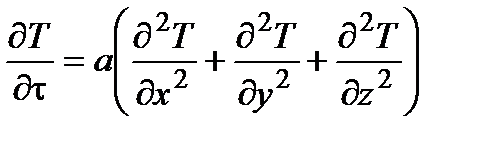Из этих уравнений видно, что скорость изменения температуры 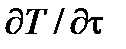в любой точке тела тем выше, чем больше значение а. Поэтому можно считать, что коэффициент температуропроводности является мерой теплоинерционных свойств материала тела. Коэффициент температуропроводности зависит только от физических параметров вещества ( 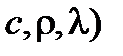и поэтому сам является физическим параметром данного вещества.

Чтобы получить решение полученных уравнений, соответствующее конкретной задаче, надо к этому уравнению присовокупить математическое описание частных особенностей данной задачи. Эти частные особенности называются краевыми условиями. К ним относятся: тепловое состояние тела в начальный момент времени (начальные условия), форма, размеры тела и особенности процесса теплообмена на его границах (граничные условия).

Ниже будут рассмотрены процессы стационарной теплопроводности в твёрдых телах простых форм.