Теплопроводность плоской стенки
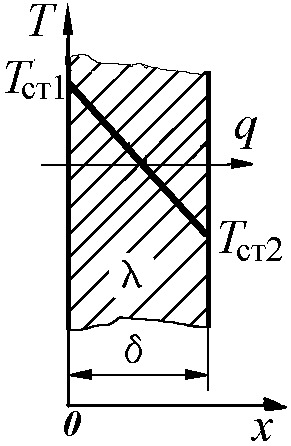
Однослойная стенка. Рассмотрим плоскую стенку (рис. 1.3) толщиной d, с коэффициентом теплопроводности 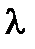 , у которой температура меняется лишь вдоль оси x, нормальной к её поверхности. Тогда изотермические поверхности являются плоскостями, перпендикулярными оси x. Пусть температуры наружных поверхностей стенки равны
, у которой температура меняется лишь вдоль оси x, нормальной к её поверхности. Тогда изотермические поверхности являются плоскостями, перпендикулярными оси x. Пусть температуры наружных поверхностей стенки равны 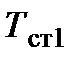 и
и 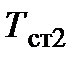 .
.
По закону Фурье в данном случае  . Интегрируя это выражение при
. Интегрируя это выражение при  const, получим формулу, описывающую температурное поле плоской стенки
const, получим формулу, описывающую температурное поле плоской стенки 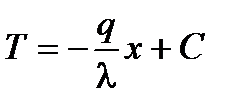 .
.
Таким образом, температура в плоской стенке изменяется по линейному закону (рис. 1.3). Используя указанные выше краевые условия: T = Т 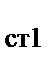 при x = 0 и T = T
при x = 0 и T = T  при x =
при x = 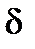 , из этого уравнения получим
, из этого уравнения получим
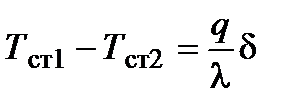 , откуда
, откуда 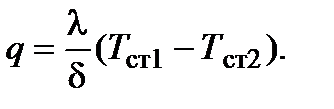
Введём обозначения:
-  - температурный напор в стенке;
- температурный напор в стенке;
- R = 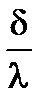 - тепловое сопротивлениестенки.
- тепловое сопротивлениестенки.
Тогда, с учётом принятых обозначений, получим 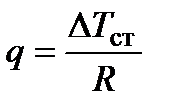 .
.
Итак, плотность теплового потока через плоскую стенку при теплопроводности пропорциональна температурному напору на стенке и обратно пропорциональна её тепловому сопротивлению.
| 
|
| Рис. 1.3 | Рис. 1.4 |
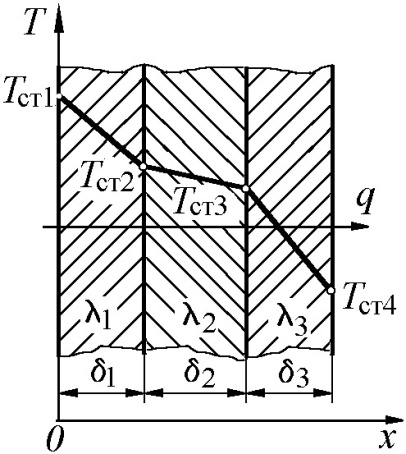
Многослойная стенка. Пусть каждый слой стенки (рис. 1.4) имеет разные коэффициенты теплопроводности ( 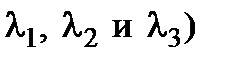 и разную толщину (
и разную толщину ( 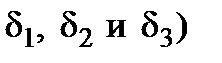 . Примем допущение, что каждый из соседних слоёв имеют одинаковую температуру. Температуры на наружных поверхностях стенки
. Примем допущение, что каждый из соседних слоёв имеют одинаковую температуру. Температуры на наружных поверхностях стенки 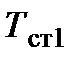 и
и 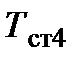 известны.
известны.
Для каждого слоя на основании выражения 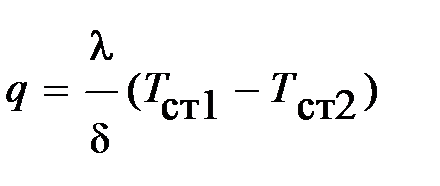 можно записать:
можно записать:
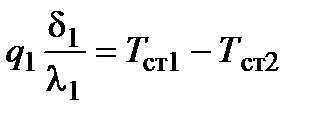 ;
;
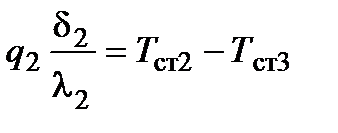 ;
;
 .
.
Просуммируем левые и правые части данных уравнений, принимая, что
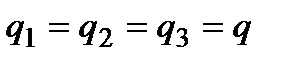 , и тогда получим
, и тогда получим
 .
.
Отсюда 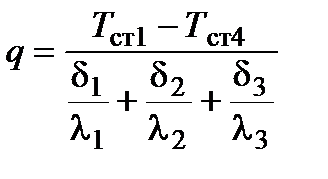 или
или  ,
,
где числитель представляет собой суммарный температурный напор, а знаменатель - полное тепловое сопротивление стенки.

|
| Рис. 1.5 |
Итак, плотность теплового потока через плоскую многослойную стенку пропорциональна суммарному температурному напору (разности температур на наружных поверхностях стенки) и обратно пропорциональна полному тепловому сопротивлению стенки, равному сумме тепловых сопротивлений ее отдельных слоёв.
Изменение температуры по сечению многослойной стенки графически представляется ломаной линией (см. рис. 9.4), причём интенсивность изменения температуры в каждом слое тем больше, чем меньше коэффициент теплопроводности данного слоя.
Определив величину q, далее, применяя для каждого слоя выражение для q, можно последовательно найти значения температур на границах соседних слоёв 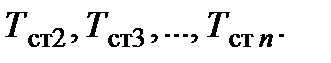
Дата добавления: 2021-06-28; просмотров: 698;











