Основное уравнение переноса субстанций
Выделим в жидкости, находящейся в движении произвольный объем V, ограниченный поверхностью S. Объем жидкости расположен в неоднородном поле физического потенциала переноса φ. Задача сводится к выводу дифференциальных уравнений, описывающих распределение скоростей, концентраций и температур во времени и пространстве, что необходимо для решения многих задач гидродинамики, тепло- и массообмена.
Процессы тепло- и массопереноса через рассматриваемую поверхность S осуществляются двумя видами механизма переноса:
- молекулярным, т.е. переносом, возникающим в результате стремления системы к термодинамическому равновесию, отклонения от которого объясняются неоднородностью поля потенциала;
- макроскопическим - конвективным переносом, вызванным наличием поля скоростей жидкости в объеме V.
B случае переноса количества движения (импульса) к указанным двум видам переноса добавляется также перенос, вызванный наличием поля гидростатического давления, а при переносе теплоты - перенос за счет теплового излучения.
Поток субстанции, вызванный стремлением системы к термодинамическому равновесию (молекулярный перенос), определяется хаотическими перемещениями молекул среды, переносящих массу, энергию и импульс и тем самым усредняющих потенциал в рассматриваемом объеме. Молекулярный перенос является определяющим в неподвижных средах и в ламинарно движущихся потоках и описывается следующими известными линейными градиентными законами.
Для переноса массы - первым законом Фика:
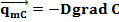
D – коэффициент молекулярной диффузии, м2/с.
Для переноса энергии (теплоты) – законом Фурье:
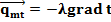
λ- коэффициент теплопроводности.
Для переноса импульса (с учетом закона внутреннего терния Ньютона):
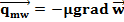
Таким образом, молекулярный перенос (плотность потока) массы qMс ‚ энергии qMt и импульса qMw описывается идентичными по форме уравнениями, которые могут быть обобщены следующим выражением:
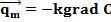
где k - коэффициент пропорциональности, в зависимости от вида переноса принимающий значение D, a (коэффициент температуропроводности a = l/(срr)) или n.
При конвективном переносе масса, энергия и импульс транспортируются в объеме макрочастиц, движущихся со скоростью w. Плотность конвективного потока 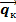 энергии или импульса на каждом участке поверхности можно выразить следующим образом:
энергии или импульса на каждом участке поверхности можно выразить следующим образом:
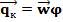
Таким образом, в случае молекулярного и конвективного переноса массы или энергии плотность потока q складывается из двух составляющих:
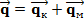
При анализе процесса переноса теплоты в правую часть этого уравнения следует добавить еще одну величину (qл)‚ учитывающую вклад в общий перенос теплоты теплового излучения.
Выделим на поверхности S, ограничивающей произвольный объем V, элемент поверхности dS. Представим его в векторной форме, умножив на единичный вектор 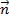 , расположенный по нормали к этому элементу и направленный из объема V:
, расположенный по нормали к этому элементу и направленный из объема V:
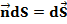
Найдем результирующий поток массы, энергии или количества движения, входящий в объем V:
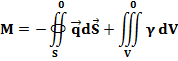
Где g - удельная объемная плотность потока.
Знак минус перед интегралом первого члена правой части этого уравнения необходим потому, что направление вектора элемента поверхности dS противоположно направлению векторов плотности входящих потоков массы, энергии и количества движения, и результирующий поток будет представлять собой разность между входящим и выходящим потоками.
Также результирующий поток массы или энергии можно найти как сумму изменения удельной объемной энергии или массы (потенциала j) во времени по всему объему V:
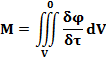
Приравняв правые части последних двух уравнений получим:

Согласно теореме Остроградского-Гаусса, интеграл от нормальной составляющей вектора по поверхности равен интегралу от дивергенции вектора по объему:
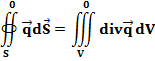
Divergentia (лат) - расхождение. Плотность потока в точке является пределом отношения потока вектора через поверхность S, ограничивающую объем V, к этому объему при его стремлении к нулю:
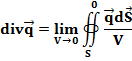
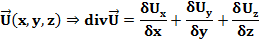
После замены получаем:
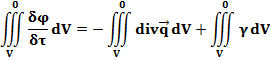
С учетом вышеизложенного уравнение принимает вид:
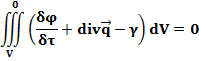
Поскольку по правилам интегрирования, интеграл будет равен нулю в том случае, если подынтегральное выражение также равно нулю, можно записать:
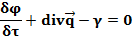
Полученное уравнение и есть основное уравнение переноса субстанций - массы, энергии и количества движения. Переписав это уравнение относительно производной потенциала по времени, получим новое выражение основного уравнения переноса субстанций:
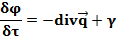
Дата добавления: 2017-03-12; просмотров: 5144;











