Условия термодинамического равновесия

Условия равновесия в процессах переноса теплоты (теплового равновесия) определяют сравнительно простыми измерениями температур соприкасающихся фаз. Механическое равновесие (при переносе импульса) обнаруживают по равенству непосредственно измеренных давлений в соприкасающихся фазах. Намного сложнее определение условия равновесия системы в процессах переноса массы. Поэтому здесь данному виду равновесия будет уделено основное внимание.

Процесс перехода массы из одной фазы в другую в изолированной замкнутой системе, состоящей из двух или большего числа фаз, возникает самопроизвольно и протекает до тех пор, пока между фазами при данных условиях (температуре и давлении) установится подвижное фазовое равновесие. Оно характеризуется тем, что в единицу времени из первой фазы во вторую переходит столько же молекул компонента, сколько из второй в первую (т.е. преимущественного перехода вещества из одной фазы в другую нет). Достигнув состояния равновесия, система может находиться в нем без количественных и качественных изменений сколь угодно долго, пока какое-либо внешнее воздействие не выведет ее из этого состояния. Таким образом, состояние изолированной системы при равновесии определяется только внутренними условиями. Поэтому градиенты интенсивных параметров и соответствующие им потоки должны быть равны нулю:

dT = 0; dP = 0; dm_i = 0

где Т - температура; Р - давление; m_i - химический потенциал i-гo компонента.

Эти выражения называют условиями соответственно термического, механического и химического (материального) равновесия. Все самопроизвольные процессы протекают в направлении достижения равновесия. Чем в большей степени состояние системы отклоняется от равновесия, тем выше скорость процесса переноса субстанций между фазами вследствие увеличения движущей силы, обусловливающей этот процесс. Поэтому для осуществления процессов переноса субстанций необходимо не допускать установления состояния равновесия, для чего к системе подводят вещество или энергию. На практике в открытых системах это условие обычно реализуется путем создания относительного движения фаз в аппаратах с противоточной, прямоточной или другими схемами движения потоков.

Из второго закона термодинамики следует, что в самопроизвольных процессах энтропия S системы возрастает и в условии равновесия достигает максимального значения, т.е. в этом случае dS = 0.

Это условие, а также три предыдущих определяют условие равновесия системы.

Химический потенциал dm_i определяется как приращение внутренней энергии U системы при добавлении к системе бесконечно малого количества молей i-гo компонента, отнесенное к этому количеству вещества, при постоянных объеме V, энтропии S и количествах молей каждого из остальных компонентов n_j (где n = l, 2, 3, …, j).

В общем случае химический потенциал может быть определен как приращение любого из термодинамических потенциалов системы при различных постоянных параметрах: энергии Гиббса G – при постоянных давлении Р, температуре Т и n_j; энтальпии H – при постоянных S, P и n_j.

Таким образом

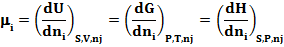
Химический потенциал зависит не только от концентрации данного компонента, но и от вида и концентрации других компонентов системы. Для смеси идеальных газов m_i зависит лишь от концентрации рассматриваемого компонента и температуры:

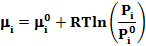
где 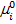-значение m_i при стандартном состоянии (обычно при Р_i = 0,1 МПа), зависит только от температуры; Р_i - парциальное давление i-гo компонента смеси; 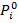– давление i-гo компонента в стандартном состоянии.

Химический потенциал характеризует способность рассматриваемого компонента к выходу из данной фазы (испарением, кристаллизацией и т.п.). В системе, состоящей из двух и более фаз, переход данного компонента может происходить самопроизвольно только из фазы, в которой его химический потенциал больше в фазу с меньшим химическим потенциалом. В условиях равновесия химический потенциал компонента в обеих фазах одинаков.

В общем случае химический потенциал может быть записан в виде:

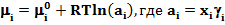
где a_i - активность i-гo компонента смеси; x_i и g_i соответственно мольная доля и коэффициент активности i-гo компонента.

Коэффициент активности g_i является количественной мерой неидеальности поведения i-гo компонента в смеси. При g_i > 1 отклонение от идеального поведения называют положительным, при g_i < 1 - отрицательным. Для отдельных систем g_i £ 1. Тогда а_i = х_i ‚ и уравнение принимает вид:

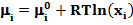
Для идеальных систем химический потенциал можно выразить также c помощью летучести f_i компонента:

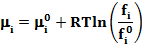
Где 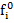-летучесть i-гo компонента в стандартных условиях. Значения величин a_i и f_i находят в справочной литературе.

При проведении технологических процессов рабочие среды (газ, пар, жидкость) находятся в неравновесном состоянии, которое не может быть описано термодинамическими параметрами. Для описания неравновесного состояния систем вводят дополнительные неравновесные, или диссипативные, параметры, в качестве которых используют градиенты интенсивных термодинамических величин - температуры, давления, химического потенциала и плотности соответствующих диссипативных потоков, связанных с переносом энергии‚ массы и импульса.

Правило фаз

Существование данной фазы в системе или равновесие фаз возможны лишь в определенных условиях. При изменении этих условий равновесие системы нарушается, происходит сдвиг фаз или переход вещества из одной фазы в другую. Возможное существование данной фазы в равновесии с другими определяется правилом фаз, или законом равновесия фаз Гиббса:

С + Ф = k + n

где C - число степеней свободы (давление, температура, концентрация) – минимальное число параметров, которые можно изменять независимо друг от друга, не нарушая равновесия данной системы; Ф - число фаз системы; k - число независимых компонентов системы; n - число внешних факторов, влияющих на положение равновесия в данной системе.

Для процессов переноса массы n = 2, так как внешними факторами в этом случае являются температура и давление. Тогда выражение принимает вид

С + Ф = k + 2

Отсюда С = k - Ф + 2.

Таким образом, правило фаз позволяет определить число параметров, которое можно менять, не нарушая фазового равновесия системы. Например, для однокомпонентной равновесной системы «жидкость – пар» число степеней свободы будет:

C = 1 – 2 + 2 = 1

T.е., в этом случае произвольно может быть задан только один параметр - давление или температура. Таким образом, для однокомпонентной системы имеется однозначная зависимость между температурой и давлением в условиях равновесия. В качестве примера можно привести широко распространенные справочные данные - зависимости между температурой и давлением насыщенных паров воды.

Для однокомпонентной равновесной системы, состоящей из трех фаз «твердое тело – жидкость – пар», число степеней свободы равно нулю: С = 1 - 3 + 2 = 0.

Например, система «вода – лед – водяной пар» находится в равновесии при давлении 610,6 Па и температуре 0,0076 °C.

Для двухкомпонентной равновесной системы «жидкость – пар» число степеней свободы С = 2 - 2 + 2 = 2. В этом случае одной из переменных величин (например, давлением) задаются и получают однозначную зависимость между температурой и концентрацией или (при постоянной температуре) между давлением и концентрацией. Зависимость между параметрами (температура - концентрация, давление - концентрация) строят в плоских координатах. Такие диаграммы обычно называют фазовыми.

Таким образом, правило фаз определяет возможность сосуществования фаз, но не указывает количественных зависимостей переноса вещества между фазами.