ОСНОВЫ ТЕОРИИ КРЫЛА
В судостроении широко используются различные конструкции, на которых возникает подъемная сила при обтекании потоком жидкости или воздуха. Наибольшее распространение получили крыльевые конструкции. Такие конструкции имеют специальную форму, обеспечивающую при обтекании их потоком подъемную силу, во много раз превосходящую силу лобового (профильного) сопротивления. На судах крылья применяют в качестве рулей, лопастей гребных винтов, лопастей крыльчатых движителей, лопаток насосов, лопастей вентиляторов
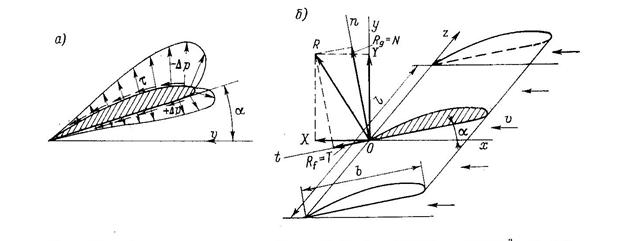
Рис. 3.21. Возникновение сил на крыле: а — эпюры давлений на элементе профиля крыла; б — схема сил на крыле У —подъемная сила; X — сила лобового сопротивления; N, Т — нормальная и тангенциальная силы соответственно
и т. д. Для выявления механизма возникновения подъемной силы рассмотрим крыло (рис. 3.21), ориентированное относительно системы координат, в которой ось х совпадает с направлением потока, ось у перпендикулярна к пей, а ось z
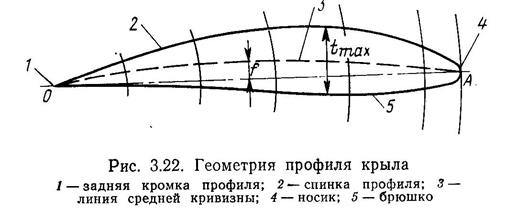
Рис. 3.22. Геометрия профиля крыла
/ — задняя кромка профиля; 2— спинка профиля; 3 — линия средней кривизны; 4 — носик; 5 — брюшко
направлена вдоль крыла. Установим некоторые терминологические понятия. Протяженность крыла в направлении оси г называется удлинением (размахом крыла) / (рис. 3.21). Если рассечь крыло плоскостью уОх, то в ее пересечении с крылом получится профиль крыла. В зависимости от требований к гидродинамическим характеристикам применяют сегментные, авиационные и другие профили (см. рис. 3. 14).
Рассмотрим геометрию профиля крыла произвольной формы (рис. 3.22). Форма профиля крыла характеризуется следующими геометрическими параметрами: относительной толщиной профиля (в процентах), т. е. отношением его максимальной толщины к хорде:
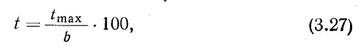 где хорда профиля b — ОА — радиус окружности, проведенной из его задней кромки 0 через крайнюю точку носика Л; относительной кривизной профиля (в процентах)
где хорда профиля b — ОА — радиус окружности, проведенной из его задней кромки 0 через крайнюю точку носика Л; относительной кривизной профиля (в процентах)
 где f — максимальная ордината кривой, соединяющей середины отрезков дуг, проведенных концеитрично из задней кромки профиля как из центра (линии кривизны профиля);
где f — максимальная ордината кривой, соединяющей середины отрезков дуг, проведенных концеитрично из задней кромки профиля как из центра (линии кривизны профиля);
средней геометрической хордой — отношением площади проекции крыла в плане 5 к его размаху: определяет нормальную силу а на ось t — тангенциальную силу T=Rf (см. рис. 3.21). Соотношения между этими составляющими следующие:
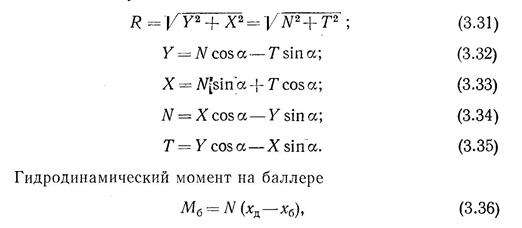 где хя — абсцисса центра давления на профиле; Хб — расстояние от начала координат до оси баллера.
где хя — абсцисса центра давления на профиле; Хб — расстояние от начала координат до оси баллера.
Гидродинамические силы Y, X, N и Т определяют продувкой крыльев в аэродинамических трубах и характеризуют с помощью следующих безразмерных коэффициентов:

Различают крылья малого, конечного и бесконечного удлинения. Если относительное удлинение крыла Л<2, то такое крыло называется крылом малого удлинения; 2<А,<6— крылом конечного удлинения, а в случае К>6 — крылом бесконечного удлинения.
Угол между направлением скорости набегающего потока и хордой крыла называется углом атаки. При движении крыла в жидкости со скоростью v под некоторым углом атаки а на верхней части профиля, называемой спинкой, будет наблюдаться сужение потока и, следовательно, увеличение скорости, а на нижней части — уменьшение скорости потока (см. рис. 3.21).
В соответствии с законом Бернулли, на спинке профиля будет наблюдаться разрежение (—Ар), а на нижней его части — повышение давления ( + Ар). Спинка профиля соответствует засасывающей, а нижняя — нагнетательной поверхности лопасти гребного винта. Разность давлений обусловливает результирующую сил давлений ЯЛ. Вязкость потока определяет наличие на профиле силы трения Rf. Результирующая этих сил R (см. рис. 3.21) называется гидродинамической силой. Проекция этой силы на ось х называется силой лобового или профильного сопротивления X, проекция силы R на ось у — подъемной силой Y. При изучении сил, возникающих на руле как на крыле, используют систему координат, связанную с крылом. В этом случае проекция равнодействующей гидр. По данным продувок крыльев и представления результатов в форме безразмерных коэффициентов для определенных значений удлинений и относительных толщин строят график зависимостей Су (а), Сх(а) или Сп(а) и Ct{a) (рис. 3.23).
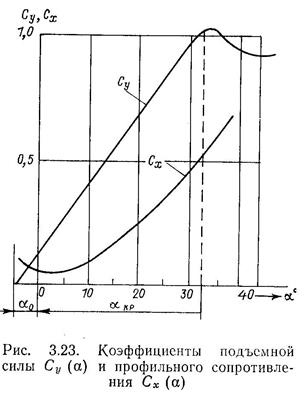
Для данного профиля коэффициенты Су, Сх, Сп и Ct являются функциями угла атаки а, а также критериев динамического подобия, т. е. чисел Fr и Re. На рис. 3.23 видно, что кривая Су(а) имеет максимум при некотором угле атаки аКр. Этот угол называется критическим. Для крыльев конечного удлинения акр = 32-^35°.
В закритических углах атаки наблюдается быстрое уменьшение Су и значительный рост Сх, т. е. наблюдается режим резкого снижения качества крыла. Это объясняется отрывом вязкого потока от спинки профиля, в результате которого нарушается плавность обтекания верхней стороны крыла и возникают вихревые дорожки за крылом. В связи с этим по Правилам Регистра СССР на судах устанавливают ограничитель угла поворота пера руля на 32°. Из рис. 3.23 видно, что при угле атаки а = 0 подъемная сила не равна нулю. Только для симметричных профилей при а=0 Су=0. Во всех других случаях Су = 0 только при каком-то отрицательном угле атаки (см. рис. 3.23), т. е. при обтекании профиля по направлению, не совпадающему с направлением хорды. Прямая, проходящая в этом направлении через заднюю острую кромку профиля, называется направлением нулевой подъемной силы (НШ1С). Угол а0 называется углом нулевой подъемной силы. Фактический гидродинамический угол атаки профиля a, = a0+aK, где ак — кромочный угол атаки, т. е. угол между хордой профиля и направлением потока.
На рис. 3.23 видно, что коэффициент подъемной силы до критического угла возрастает по закону, близкому к линейному,
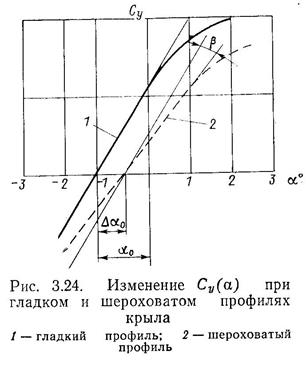
В процессе эксплуатации судна изменяется состояние поверхности наиболее ответственных механизмов и устройств, работающих по принципу крыла, и в первую очередь лопастейодинамической силы на ось п гребного винта и руля. Изменение толщины и характера распределения пограничного слоя при обтекании профиля вследствие шероховатости вызывает уменьшение подъемной силы. Из-за различного отклонения линии тока на спинке и брюшке профиля уменьшается эффективная кривизна средней линии профиля по сравнению с геометрической fc = f/b, и тем больше, чем толще пограничный слой. В результате этого уменьшается угол нулевой подъемной силы ао- Одновременно уменьшается тангенс угла наклона кривой Су (<ц), увеличивается сила профильного сопротивления и снижается подъемная сила (рис. 3.24).
§ 23. ОСНОВЫ
ЛОПАСТНОЙ ТЕОРИИ ГРЕБНОГО ВИНТА
Для того чтобы гребной винт мог приводить в движение судно, необходимо передать ему от главного двигателя через гребной вал некоторый крутящий момент М при частоте вращения п. При проходе через диск винта массы воды воспринимают воздействие момента М и получают, следовательно, приращение момента количества движения относительно оси винта; поэтому поток жидкости за винтом закручивается в сторону его вращения, т. е. в нем кроме вызванных осевых скоростей wa на бесконечности за винтом и wa/2 в диске винта (в соответствии с теоремой Фруда — Финстервальдера) возникают также и окружные вызванные скорости wt на бесконечности.
Из теории гребного винта известна связь между осевыми и
окружными вызванными скоростями wt 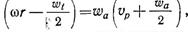 т. е. вызванная идеальным гребным винтом окружная скорость в плоскости его диска равна половине вызванной скорости за винтом и направлена в сторону, противоположную окружной скорости потока.
т. е. вызванная идеальным гребным винтом окружная скорость в плоскости его диска равна половине вызванной скорости за винтом и направлена в сторону, противоположную окружной скорости потока.
Рассмотрим многоугольник скоростей потока, натекающего па кольцевой элемент лопасти винта, толщиной dr, образованный сечениями винта двумя соосными с ним цилиндрами радиусами г и r+dr (рис. 3.25). Очевидно, что этот элемент можно рассматривать как элемент крыла, расположенный в потоке жидкости под дикулярными сторонами этого многоугольника являются окружная скорость ыг:2лгп, обусловленная вращением гребного винта, и осевая скорость vp, вызванная поступательным движением элемента лопасти в жидкости в направлении движения судна.
Соответственно угол 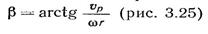 называется углом поступи.
называется углом поступи.
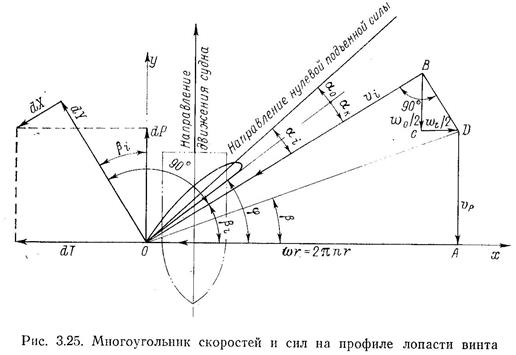
Третьей стороной многоугольника скоростей, расположенной по нормали к замыкающей стороне — вектору результирующей скорости натекающего потока, равному
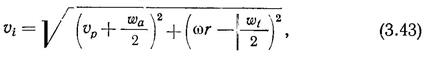
является результирующая вызванная скорость в диске винта
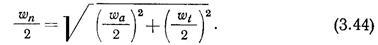
Поскольку углы Pi = АОВ и CBD равны, то угол р, определится формулой
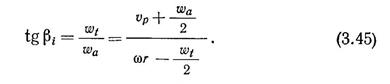
с учетом индуктивных потерь, являющихся следствием появления вызванных скоростей wa и wt.
Направление вектора результирующей скорости Vi и хорды элемента лопасти определяют три угла, показанных на рис. 3.25: угол атаки элемента лопасти щ, кромочный угол ак, угол нулевой подъемной силы .
В соответствии с теорией крыла на рассматриваемом элементе лопасти возникнут сила профильного сопротивления dX, направленная вдоль вектора скорости v, и перпендикулярная к ней подъемная сила dY. Проецируя эти силы па ось Ох, совпадающую с направлением окружной скорости элемента лопасти, и перпендикулярную к пей ось Оу, совпадающую с направлением поступательной скорости винта, получаем соответственно элементарные упор и касательную силу
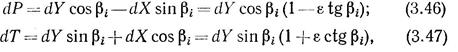
где e =--обратное количество элемента лопасти
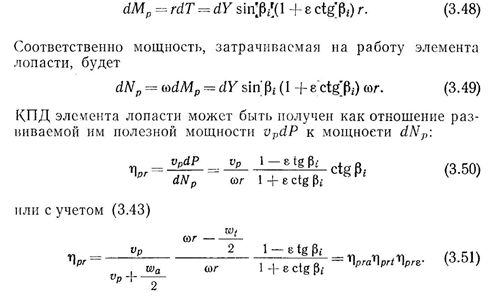
Первый и второй сомножители в выражении (3.51) характеризуют потери на вызванные скорости wa и wt\ третий сомножитель — профильное сопротивление и потери, обусловленные конструктивными особенностями элемента лопасти.
Подставляя в формулы (3.46) и (3.48) выражение для подъемной силы крыла,

заменяя в нем площадь dF площадью элемента лопасти и интегрируя полученные выражения с учетом числа лопастей в пределах от радиуса ступицы гстдо внешнего радиуса винта R, получаем выражения для полных упора Р и момента сопротивления Мр гребного винта
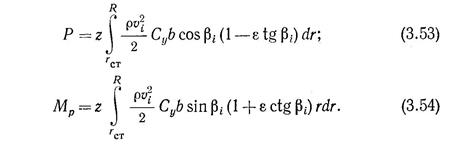
Для преодоления момента Мр к гребному винту должен быть приложен равный по величине и обратный по направлению крутящий момент, развиваемый главным двигателем. Равенство, этих моментов обусловливает вращение гребного винта с постоянной частотой.
При вращении гребного винта на его лопастях, как на крыльях, наряду с моментом возникает сила упора, приложенная вдоль оси вала к упорному подшипнику, жестко связанному с корпусом судна. Эта сила, уравновешивая силу сопротивления среды, придает судну поступательное движение.
Гидродинамические характеристики гребного винта.Упор Р и момент Мр являются гидродинамическими характеристиками гребного винта, выраженными в размерной форме. Однако в теории и практике проектирования и эксплуатации гребных винтов, как правило, используют безразмерные гидродинамические характеристики, для определения которых интегральные выражения (3.53) и (3.54) представляют в безразмерной форме, приводя к ней все члены подынтегральных выражений:
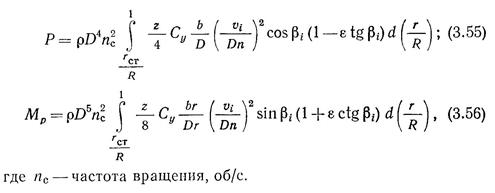
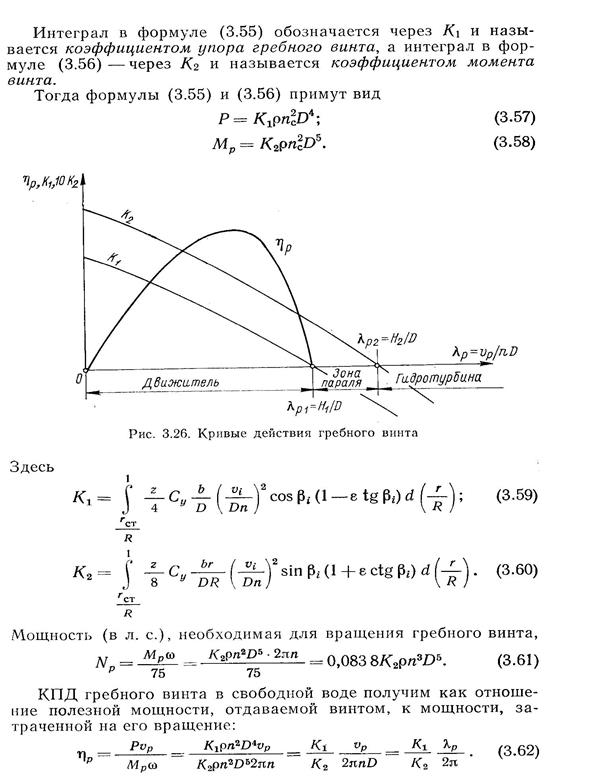
„Безразмериые гидродинамические характеристики r\p, К\, К2, представленные графически в зависимости от относительной поступи Кр, называются кривыми действия гребного винта в свободной воде (рис. 3.26). Для геометрически подобных гребных винтов и их моделей при соответствующих состояниях поверхностей лопастей и ступиц кривые действия в свободной воде тождественны.
Дата добавления: 2017-03-12; просмотров: 6844;











