ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАБОТЫ ГРЕБНЫХ ВИНТОВ В СВОБОДНОЙ ВОДЕ

<3 4 567 8 9 >

Изучение гребных винтов, накопление исходных материалов для практических расчетов и решение многих эксплуатационных задач, связанных с гребными винтами, базируется на экспериментальных данных, полученных на основе испытаний моделей винтов.

При проведении таких экспериментов винты и их модели должны быть геометрически, кинематически и динамически подобны. В § 9 установлено, что при соблюдении динамического ПОДОБИЯ:

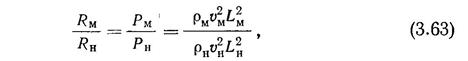
где Р — сила упора винта и модели; L характеризует линейные размеры винта и модели, т. е. их диаметры D, а скорость v определяется скоростью вращения винта nnD. Тогда

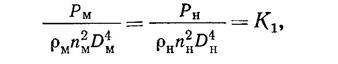
и аналогично можно получить К₂ .

Таким образом, при соблюдении динамического подобия коэффициенты К₁ и К2 должны быть одинаковыми для модели гребного винта и его натуры. Динамическое подобие предполагает наличие геометрического подобия, т. е. у натурного винта и его модели должны быть равны дисковые отношения θ, число лопастей z, относительные толщины, шаговое отношение при одинаковом контуре лопасти. Должны быть пропорциональны линейные размеры и т. д.

Из условия кинематического подобия вытекает постоянство отношений сходственных скоростей. Например, отношение поступательной скорости v_p к окружной скорости n_cD у натурного винта и модели должно быть одинаковым, т. е.

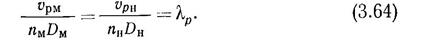
Следовательно, у геометрически подобных гребных винтов динамическое подобие существует только при равенстве их относительных поступей λрм=λ_Рн-

В соответствии с теорией подобия необходимо, чтобы, кроме того, для модели и натурного винта были равны числа Рей-польдса. При испытаниях модели и в условиях эксплуатации натурного винта коэффициенты кинематической вязкости среды практически равны (v_M = v_n). Тогда равенство чисел Рейнольдса может быть представлено в форме

Заменяя скорости с_м и v_n окружными скоростями концов лопастей, получаем

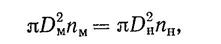
Откуда

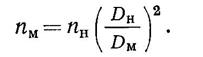
Упор модели при этом будет равен упору натурного винта, т. е.

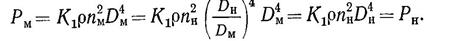
Установлено, однако, что если проводить испытания моделей гребных винтов с числами Рейнольдса, которые на 10— 20% выше критических, то получаются стабильные результаты и надежные данные эксперимента.

Числа Рейнольдса для винтов подсчитываются как

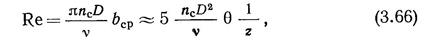
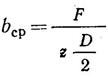-средняя относительная ширина лопасти. Кри-

тпческое число Рейнольдса для гребных винтов (Re)_I_!_p=(3-5) 10⁵.

С учетом этих факторов осуществляют испытания систематических серий моделей гребных винтов в бассейнах и специальных лабораторных установках, называемых кавитационными трубами. Эти испытания позволяют установить взаимосвязь всех геометрических характеристик {HID; 0; z; d_CT/D и др.) и их влияние на эффективность работы гребных винтов. Помимо этого, систематические испытания моделей гребных винтов позволяют получить исходный материал для построения специальных диаграмм, с помощью которых выбирают геометрические элементы винтов при их проектировании и решают все практические задачи по ходкости судна, связанные с работой гребных винтов.

Испытания моделей гребных винтов заключаются в измерении упора Р и момента М_р гребного винта при различных частотах вращения п и различной скорости поступательного движения v_p. Результаты испытаний обрабатываются в виде кривых действия гребного винта (см. рис. 3.26). Серии моделей винтов обычно варьируются по H/D, θ, z при сохранении контура лопастей, формы лопастных сечений, их относительной толщины и относительного диаметра ступицы. Кривые действия гребного винта позволяют решать проектные и эксплуатационные задачи, причем обычно достаточно располагать кривыми ƞ_Р = λ_Р и К₂=(λ_Р) либо Kz = f(λ_Р)и ƞ_Р =(λ_р) в зависимости от того, какая задача решается.

В мировой практике для этих целей широко используются диаграммы, построенные на основе кривых действия гребных винтов. Оригинальная форма таких диаграмм, получившая признание в нашей стране, предложена Э. Э. Папмелем. Существо ее заключается в том, что на кривых действия серийных винтов соединяются точки с одинаковым значением КПД на линиях К₁= (λ_Р) и K₂=(λ_P), В результате получаются две диаграммы— одна для решения задач, когда выбирается двигатель, другая — обратная, когда его характеристики известны и для них с помощью диаграммы рассчитываются элементы винта н скорость судна. По обеим диаграммам легко определить оптимальные диаметр винта или частоту его вращения, скорость судна или упор винта, его шаговое отношение, потребляемую мощность двигателя и т. д. Если диаметр или частота вращения неизвестны, то такую задачу можно решить методом последовательных приближений. Для облегчения решений задач с помощью диаграмм Папмелем был предложен ряд расчетных коэффициентов, позволяющих в зависимости от условия задания решать прикладные задачи по ходкости судна. Упомянутые условия и расчетные коэффициенты, с помощью которых они решаются, сведены в табл. 3.1.

На рис. 3.28 представлены схема построения диаграммы и се общий вид. Схема построена в координатах К₁— λ_Р; что вторая половина диаграммы, в координатах К₂—λ_Р

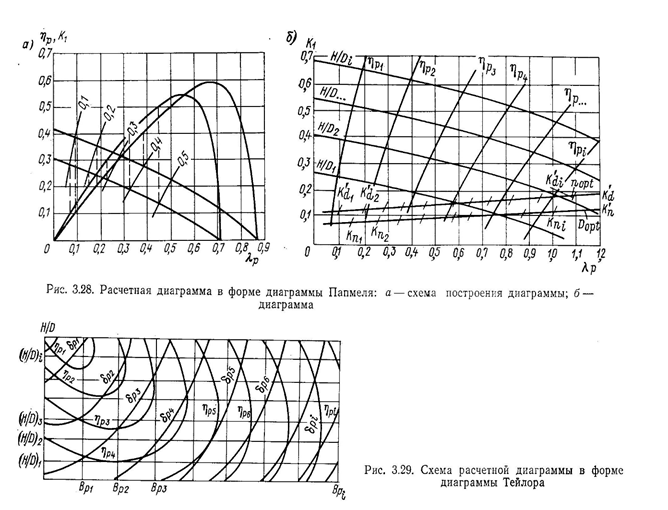
будет по своему виду аналогичной. На рис. 3.28, а показана схема построения диаграммы на базе кривых действия и линий постоянных КПД, на рис. 3.28, б — схема одной половины расчетной диаграммы К₁(λ_Р). Аналогичную форму имеют диаграммы многих серий винтов, обработанные или перестроенные в виде диаграмм Папмеля. На основе расчетных коэффициентов на диаграмме нанесены геометрические места точек максимального КПД гребного винта и определены линии оптимального диаметра D_ОПТ и оптимальной частоты вращения n_опт.

В зарубежной практике применяется другая форма представления расчетных диаграмм гребных винтов, предложенная Тейлором.

Наиболее широко известная зарубежная серия гребных винтов была испытана Троостом в голландском опытовом бассейне в Вагенингене. Исходными для этой серии были приняты модели с саблевидным контуром лопастей, авиационными сечениями у корня лопасти и сегментными на периферийных радиусах. В серию входили модели с числом лопастей Z = 2-6 и с дисковыми отношениями θ = 0,3-0,7. Диаграммы в форме диаграмм Тейлора строят в виде зависимостей общепринятых за рубежом коэффициентов нагрузки по мощности

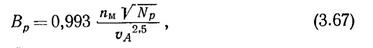
обратной относительной поступи

и КПД винта ƞ_Р, где п_М— частота вращения, об/м; N_p— мощность на валу у винта, л. с; v_A = v_s(1-Ψ)—скорость в диске винта, уз; 0,993 и 3,28 — числовые коэффициенты перевода в метрические меры (рис. 3.29).

Кривые действия гребного винта в этих диаграммах приводятся отдельно. На расчетных диаграммах строятся также линии оптимальных значений диаметра и частоты вращения гребных винтов.

Для решения проектных задач, в которых необходимо определить потребную мощность главного двигателя, в диаграммах Тейлора используется коэффициент нагрузки по упору

где Р — упор, кгс.

Для эксплуатационного анализа работы гребных винтов и построения паспортных диаграмм используются диаграммы в координатах μ — σ и μ — φ, где расчетные коэффициенты

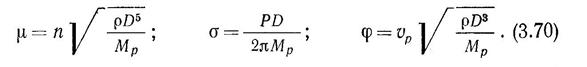
Схемы расчетов, связанных с выбором геометрических характеристик гребных винтов, определением потребной мощности судовой энергетической установки, анализом данных эксплуатации энергетической установки через винт, паспортных диаграмм и др., приводятся в учебно-методических пособиях.

<3 4 567 8 9 >

Дата добавления: 2017-03-12; просмотров: 4765;