Судовые магнитные силы
Результирующий вектор горизонтальной составляющей напряженности судового магнитного поля в районе картушки магнитного компаса удобно представлять его отдельными компонентами, которые получили название судовых магнитных сил (СМС). Состав этих сил и их взаимную ориентацию можно определить, используя равенства (4.12), в которых левые и правые их части следует умножить на 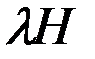 . В результате будем иметь:
. В результате будем иметь:
 (4.17)
(4.17)

| Важно! |
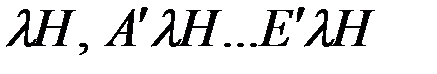 , входящие в полученное уравнение. Анализируя указанные коэффициенты, обратим внимание на то обстоятельство (см. равенства (4.9)), что СМС
, входящие в полученное уравнение. Анализируя указанные коэффициенты, обратим внимание на то обстоятельство (см. равенства (4.9)), что СМС 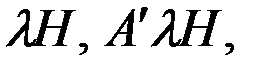
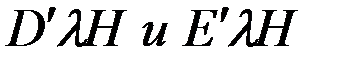 зависят от параметров и расположения на судне магнитомягких материалов, а СМС
зависят от параметров и расположения на судне магнитомягких материалов, а СМС 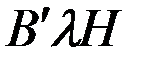 и
и 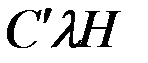 - как магнитомягких, так и магнитотвёрдых. Также нетрудно заметить, что первая группа СМС зависит от величины горизонтальной составляющей Н напряженности магнитного поля Земли, в то время как вторая группа – от вертикальной составляющей Z. Все СМС не зависят от курса судна. Поскольку СМС представляют собой компоненты вектора напряжённости судового магнитного поля, они также являются векторными величинами.
- как магнитомягких, так и магнитотвёрдых. Также нетрудно заметить, что первая группа СМС зависит от величины горизонтальной составляющей Н напряженности магнитного поля Земли, в то время как вторая группа – от вертикальной составляющей Z. Все СМС не зависят от курса судна. Поскольку СМС представляют собой компоненты вектора напряжённости судового магнитного поля, они также являются векторными величинами.
Для определения ориентации СМС обратимся к равенствам (4.17).
Будем условно полагать, что все СМС, кроме 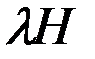 и
и 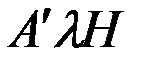 , равны нулю.
, равны нулю.
В этом случае указанные равенства примут вид:
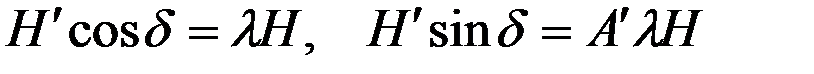 (4.18)
(4.18)
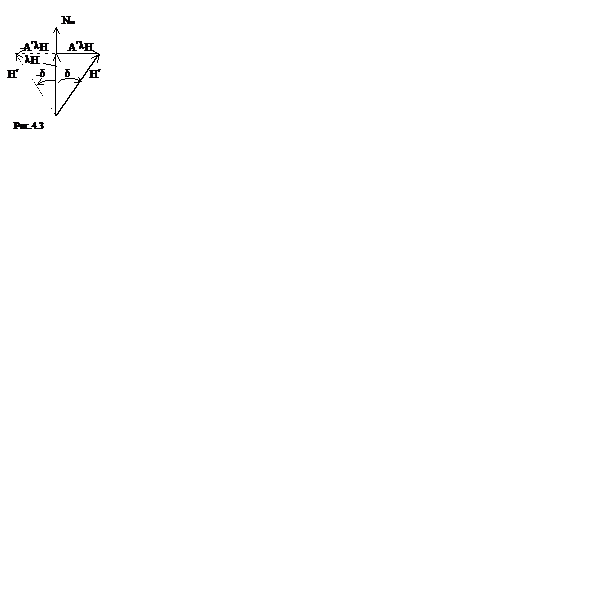 Из них следует, что вектор
Из них следует, что вектор 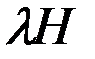 равен проекции результирующего вектора Н¢ напряжённости судового магнитного поля на направление магнитного меридиана (рис. 4.3), а вектор
равен проекции результирующего вектора Н¢ напряжённости судового магнитного поля на направление магнитного меридиана (рис. 4.3), а вектор 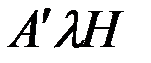 - на направление, перпендикулярное магнитному меридиану. При этом, если δ > 0, то СМС
- на направление, перпендикулярное магнитному меридиану. При этом, если δ > 0, то СМС 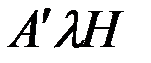 ориентирована на Восток, в противном случае, как это показано штриховыми линиями, – на Запад. Очевидно, будучи направленной воль магнитного меридиана, СМС
ориентирована на Восток, в противном случае, как это показано штриховыми линиями, – на Запад. Очевидно, будучи направленной воль магнитного меридиана, СМС 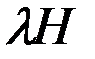 является полезной, стремящейся установить картушку магнитного компаса в этот меридиан. Поэтому следует стремиться сделать коэффициент
является полезной, стремящейся установить картушку магнитного компаса в этот меридиан. Поэтому следует стремиться сделать коэффициент 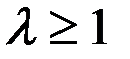 .
.
Для того чтобы определить направление СМС 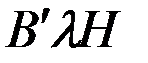 , будем условно считать, что в равенствах (4.17) все СМС, кроме
, будем условно считать, что в равенствах (4.17) все СМС, кроме 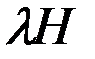 и
и 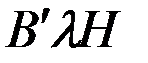 , равны нулю. Тогда, указанные выражения примут вид:
, равны нулю. Тогда, указанные выражения примут вид:
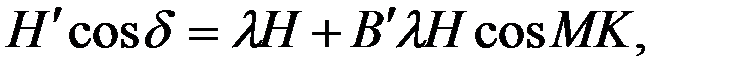
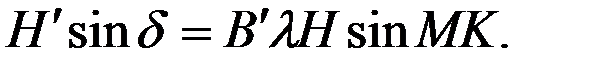 (4.19)
(4.19)
Этим равенствам соответствует схема векторов, показанная на рис. 4.4. Из рисунка следует, что СМС 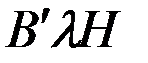 направлена по курсу судна. Действительно, только в этом случае ее проекция на направление магнитного меридиана и на перпендикулярное к нему направление будет определяться выражениями (4.19).
направлена по курсу судна. Действительно, только в этом случае ее проекция на направление магнитного меридиана и на перпендикулярное к нему направление будет определяться выражениями (4.19).
Поступая аналогично, определим направление СМС С¢lН. Для этого будем полагать неравными нулю только силы lН и С¢lН. Тогда получим:
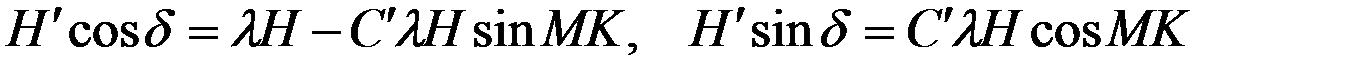 . (4.20)
. (4.20)
Схема векторов, соответствующая равенствам (4.20), имеет вид, показанный на рис. 4.5. Из рисунка следует, что СМС С¢lН направлена под углом 900+МК по отношению к магнитному меридиану и, следовательно, перпендикулярно СМС В¢lН.
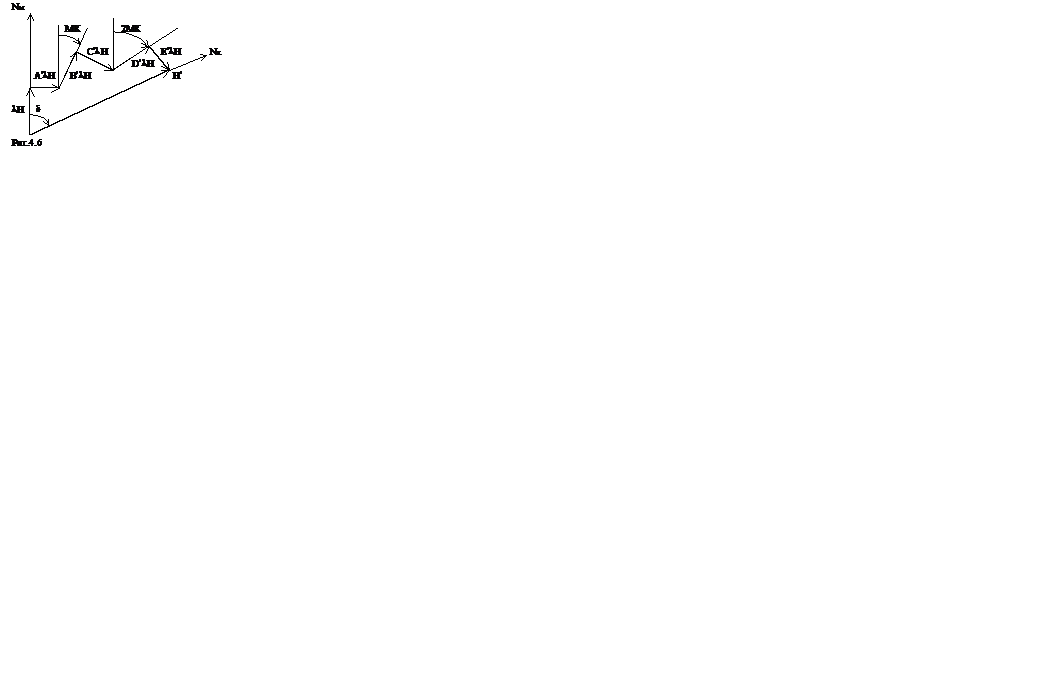

Учитывая, что выражения для D¢lH и Е¢lH отличаются от рассмотренных только удвоенным значением МК, можно утверждать, что СМС D¢lH направлена под углом 2МК к направлению магнитного меридиана, а СМС Е¢lH - под углом 2МК+900 по отношению к магнитному меридиану или перпендикулярно судовой магнитной силе D¢lH.
Таким образом, в общем случае ориентация векторов судовых магнитных сил будет иметь вид, показанный на рис. 4.6. На этом рисунке Nk
соответствует направлению компасного меридиана, в плоскости которого находится результирующий вектор Н¢ напряжённости судового магнитного поля. Проектируя векторы СМС на направление компасного меридиана, найдём выражение, определяющее значение вектора Н¢:
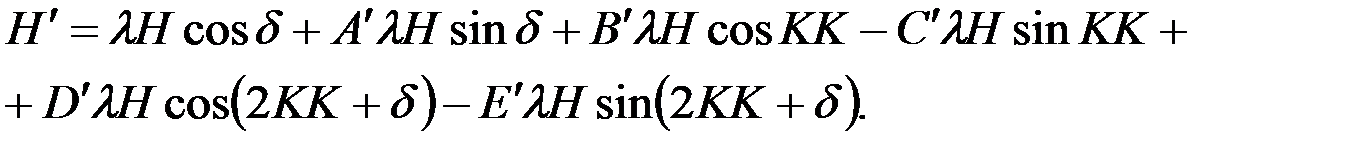
Дата добавления: 2017-02-13; просмотров: 3195;











