Основные характеристики земного и судового магнитных полей. Уравнения Пуассона и А. Смитта. Судовые магнитные силы (СМС)

Общая характеристика земного магнитного поля

2

N_и

N_м

о

1

3

S_м

S_и

Т

Рис.1.1

Земное магнитное поле может быть приближённо представлено как поле некоторого постоянного магнита 1 (рис. 1.1), полюса которого расположены вблизи полюсов Земли.* Плоскости 2, образованные магнитными силовыми линиями, являются плоскостями магнитных меридианов, а касательные к магнитным силовым линиям определяют направление векторов Т напряжённости магнитного поля Земли.

N_м

N_и

о

Н

Т

I

-d

Z

n

E_и

.1.2

Плоскость 3 магнитного экватора перпендикулярна оси, соединяющей между собой северный N_м и южный S_м магнитные полюсы§. Очевидно, что из-за несовпадения географических полюсов N_и и S_и с магнитными полюсами Земли, плоскости географических меридианов и экватора также не будут совпадать с плоскостями магнитных меридианов и экватора. Угол d, определяющий отклонение в плоскости горизонта магнитного меридиана относительно истинного (рис. 1.2), называется магнитным склонением и может изменяться в пределах .

Рис.1.2

Вектор Т напряжённости магнитного поля Земли лежит в плоскости магнитного меридиана и составляет с плоскостью горизонта некоторый угол I. Этот угол называется магнитным наклонением и может изменяться в пределах .

Наряду с указанным, рассматривают проекции Н и Z вектора Т на плоскость горизонта и на местную вертикаль, соответственно. Эти составляющие определяются следующими равенствами:

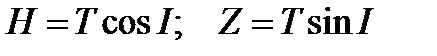. (1.1)
На навигационных картах могут наноситься линии равных значений указанных параметров. Изогонами называют линии равных значений магнитного склонения. Линии равных значений магнитного наклонения получили название изоклин. Линии равных значений Н и Z называются изодинамами.

Земное магнитное поле претерпевает медленное годовое изменение, а также достаточно быстрые вариации, обусловленные, например, активизацией процессов на Солнце. Кроме того, на равномерность магнитного поля Земли существенное влияние оказывают местные магнитные аномалии.

магнитомягкие материалы намагничиваются компонентами магнитного поля Земли. Будем представлять судовое и земное магнитные поля в виде соответствующих составляющих X¢,Y¢,Z¢ и X,Y,Z (рис. 4.1) векторов напряженности (или индукции) этих полей по осям системы координат охуz, жёстко связанной с судном. Особенности намагничивания магнитомягких материалов земным магнитным полем заключается в том, что они будучи намагниченными од

Важно!

ной из компонент этого поля, например компонентой Х, создают свое поле, имеющее, общем в случае, все три компоненты, величины которых пропорциональны намагничивающему полю. Таким образом, при намагничивании материала компонентой Х сам намагниченный материал создаёт поле, имеющее со ставляющие аХ, dХ и gХ, направленные по осям ох, оу и oz, соответственно (Рис. 4.1). Здесь а, d и g – коэффициенты пропорциональности, определяющие величину указанных составляющих в долях намагничивающего поля. Аналогично, материал, намагниченный составляющей Y земного поля, будет создавать собственное поле с компонентами bY, eY и hY, а намагниченный составляющей Z – с компонентами cZ, fZ и kZ.

Учитывая сказанное, результирующие напряженности судового магнитного поля вдоль осей, связанных с судном, можно представить в виде следующих равенств (рис. 1.33):

X¢ = X + aX + bY + cZ + P,

Y¢ = Y + dX + eY +fZ + Q, (4.1)

Z¢ = Z + gX + hY + kZ + R,

где H, Q и R – компоненты магнитного поля, порождаемые постоянным судовым магнетизмом. Уравнения (4.1) получили название уравнений Пуассона, а коэффициенты а…к – коэффициентов Пуассона. Полученные уравнения характеризуют структуру судового магнитного поля и являются исходными для проведения различных оценок на практике. Однако для процесса судовождения основной интерес представляет связь параметров судового поля с ошибками МК, т.е. с той девиацией, которая возникает у компаса, установленного в заданном месте на судне. Эта девиация определяется отклонением от плоскости магнитного меридиана горизонтальнойсоставляющей Н¢ (рис. 4.1) судового магнитного поля, образуемой геометрической суммой векторов X¢ и Y¢, в направлении которой устанавливаются оси магнитов картушки компаса. Найдём соотношения, определяющие указанную связь.

Уравнение девиации

Рассмотрим рис. 4.2, отображающий взаимную ориентацию векторов судового и земного магнитных полей. Как следует из рисунка, девиация 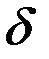магнитного компаса, равная разности магнитного МК и компасного КК курсов судна

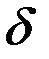=МК – КК , (4.2)

может быть определена следующим равенством:

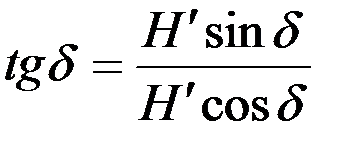. (4.3)

В свою очередь, из рисунка следует, что

H¢sin 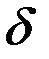=X¢sin MK + Y¢cos MK, а H¢cos 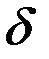=X¢cos MK – Y¢sin MK. (4.4)

Подставляя в полученные равенства значения X¢ и Y¢ из уравнений Пуассона (4.1), найдём:

H¢sin 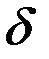=[(1+a)X + bY + cZ + P] sin MK + [(1+e)Y + dX + fZ +Q] cos MK,

H¢cos 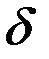=[(1+a)X + bY + cZ + P] cos MK – [(1 + e)Y +dX + fZ = Q] sin MK.

(4.5)

В последних равенствах учтём, что

Х=Н cosMK, Y= - H sinMK. (4.6) Тогда получим:

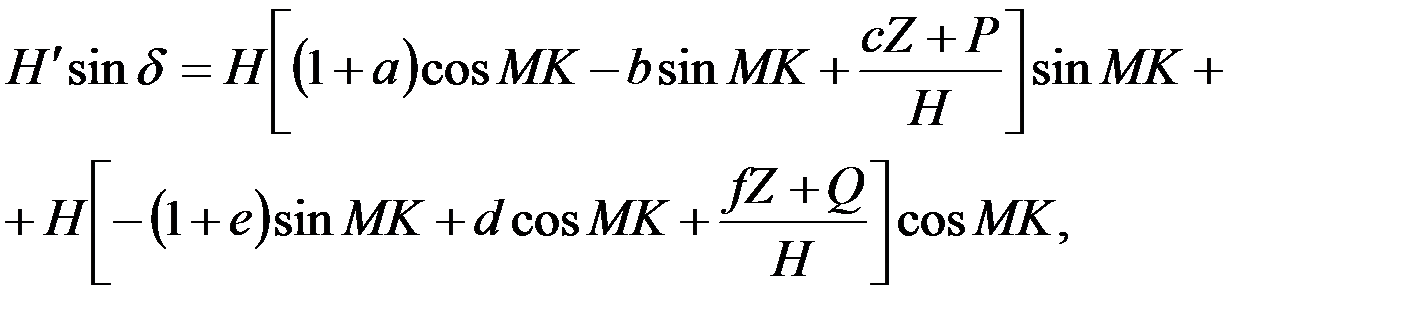
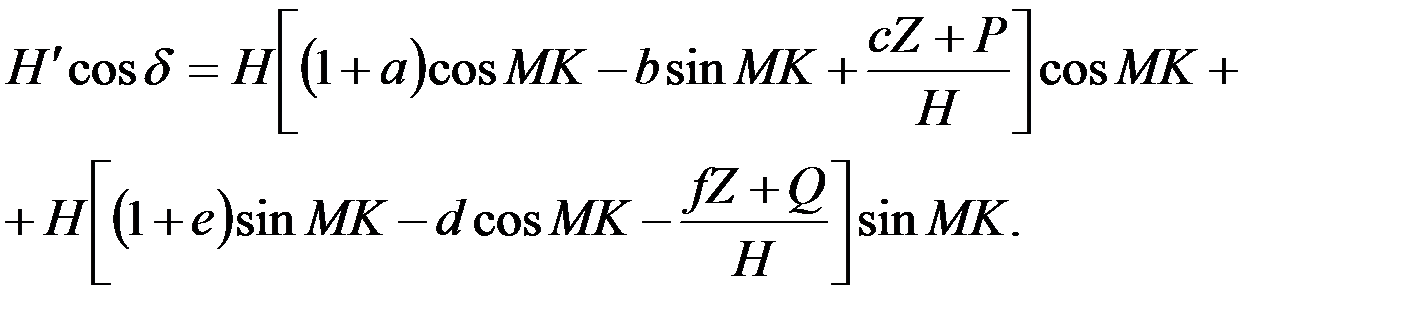(4.7)

Раскрывая квадратные скобки равенств (4.7), найдём:

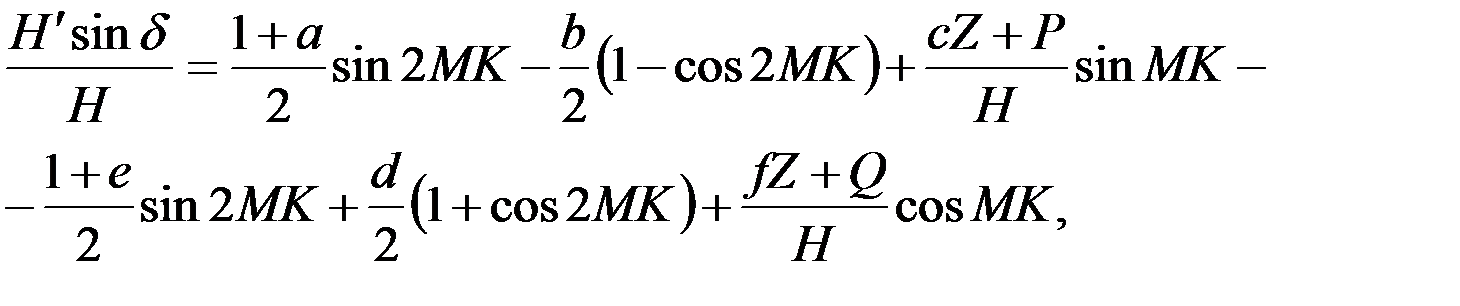
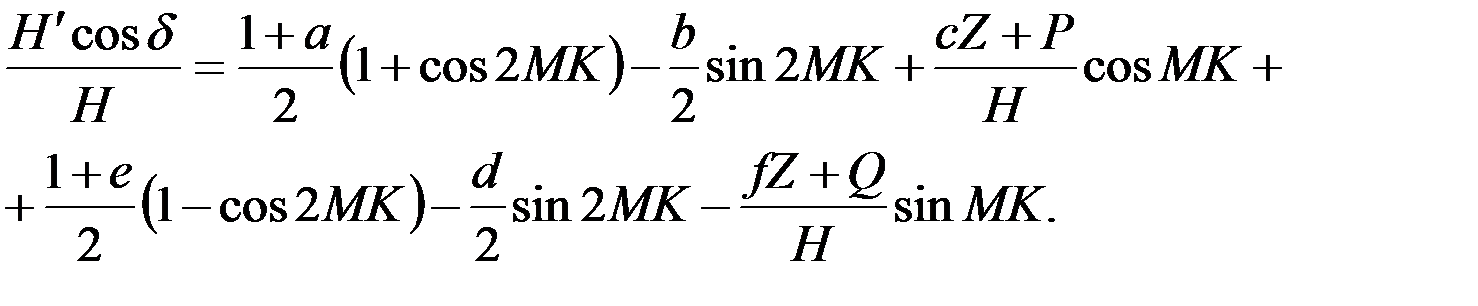(4.8)

Группируя члены по гармоникам, будем иметь:

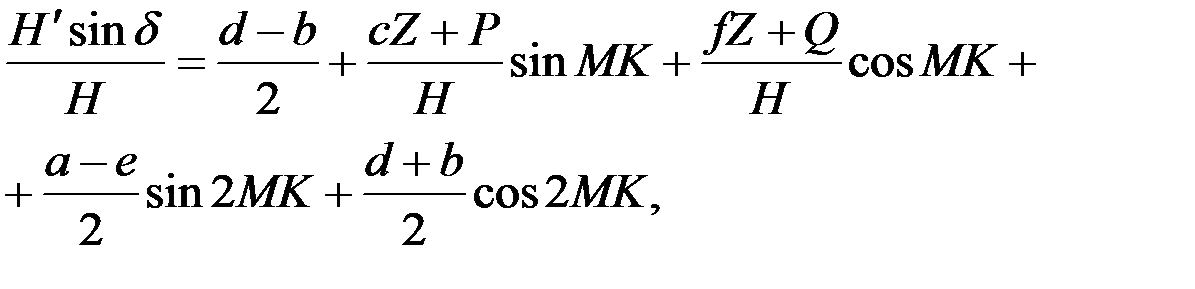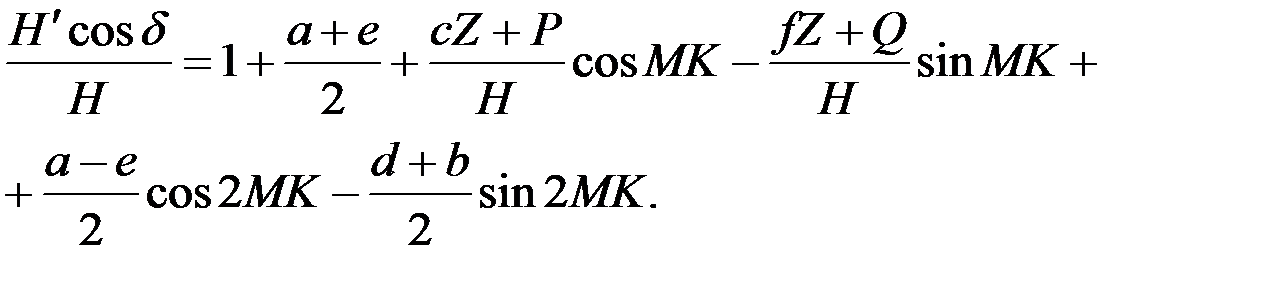(4.9)

Обозначим 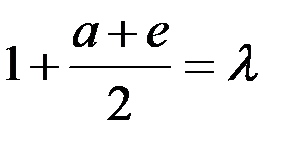и поделим левые и правые части равенств (4.9) на 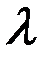. В результате получим:

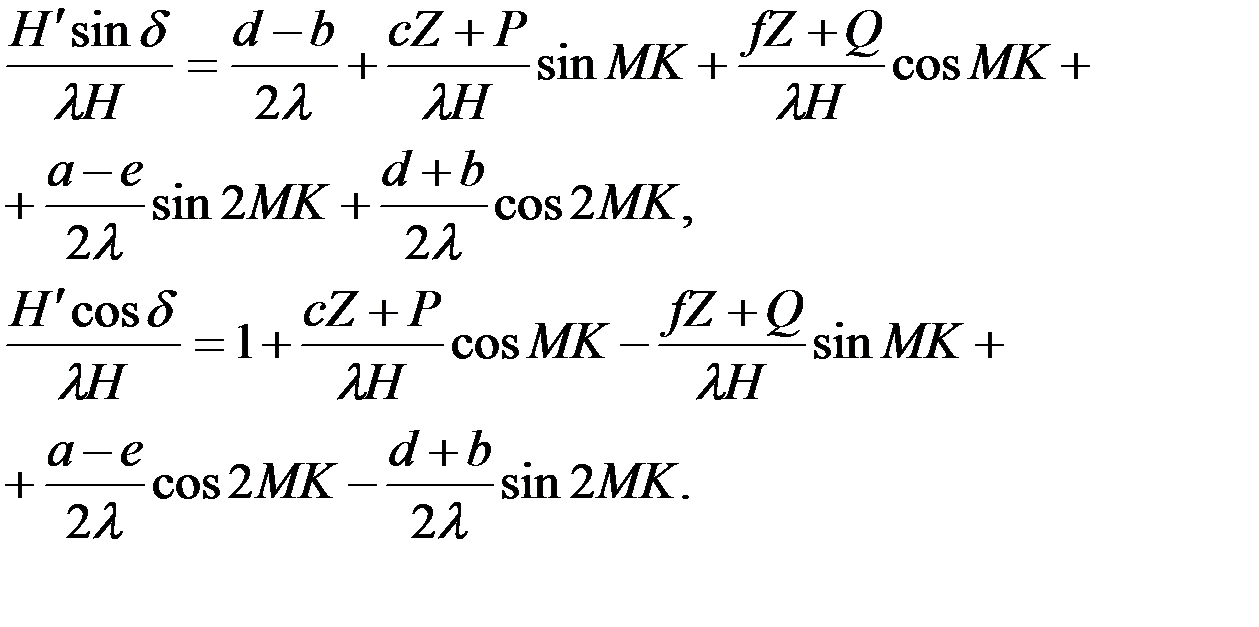(4.10)

Введём следующие обозначения:

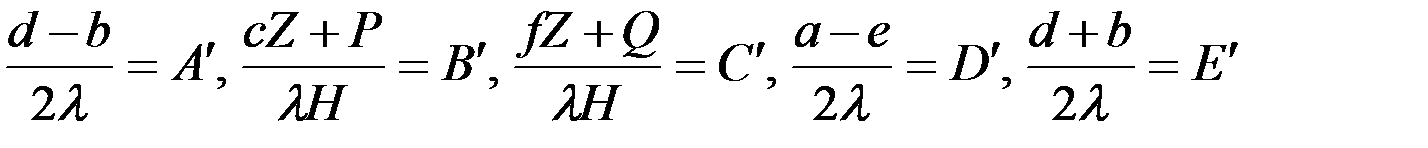(4.11)

и подставим их в равенства (4.10). В результате будем иметь:

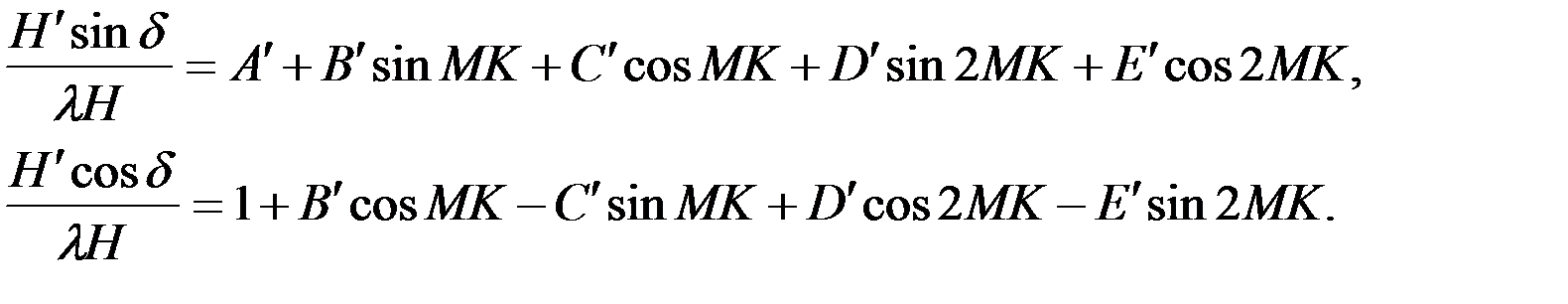
(4.12)

Поделив первое равенство (4.12) на второе, получим искомое выражение для тангенса девиации магнитного компаса:

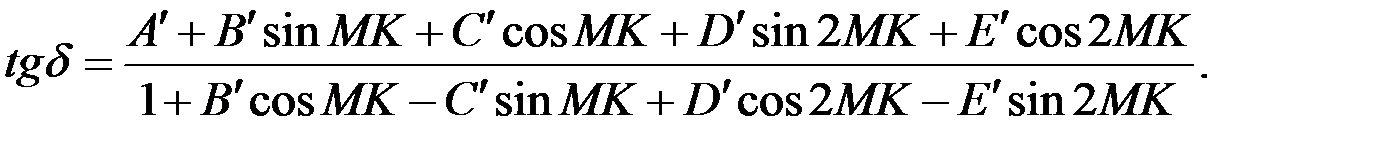
(4.13)

Это выражение получило название формулы Арчибальда Смита по имени английского учёного Х1Х века. Оно определяет зависимость девиации МК от параметров А¢…E¢ и магнитных курсов судна. Параметры A¢…E¢ получили название коэффициентов девиации.

На практике чаще представляют девиацию МК в функции компасных курсов судна [5]. Для того чтобы получить указанное выражение умножим равенство (4.13) на его знаменатель. В результате будем иметь:

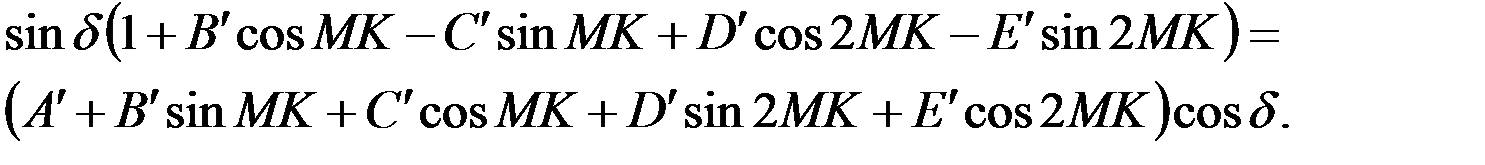(4.14)

Раскрывая скобки и перенося все члены кроме первого в правую часть равенства, найдём:

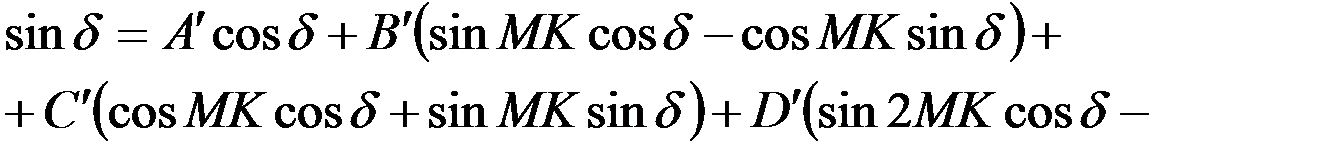
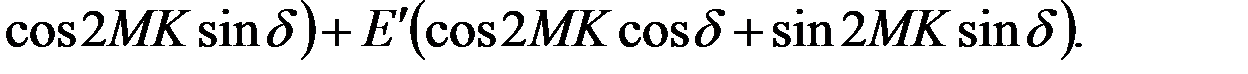(4.15)

Учитывая, что КК=МК - 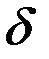, а 2МК-δ = 2КК+ 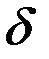, окончательно получим выражение для синуса девиации магнитного компаса как функцию компасных курсов судна:

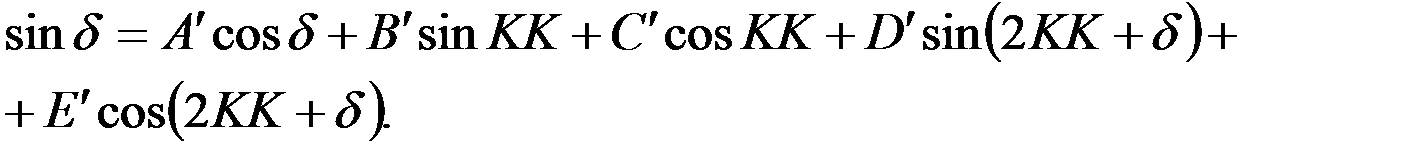(4.16)

Важно!

Таким образом, определены выражения, характеризующие закон изменения девиации МК и позволяющие дать её численную оценку в различных условиях плавания. Большее распространение для решения указанной задачи получило равенство (4.16). Однако, какое бы равенство не использовалось при выполнении оценок, следует иметь в виду (см. соотношения 4.11), что коэффициенты девиации А¢,D¢ и E¢ практически не зависят от места судна, а коэффициенты B¢ и C¢ изменяются с изменением широты места судна, так как от указанного параметра зависит горизонтальная составляющая Н напряжённости магнитного поля Земли. Из тех же выражений видно, что коэффициенты девиации не зависят от курса судна.