А поскольку нет силы обеспечивающей боковое смещение , то все остальное построено исключительно на фантазиях.
Версия Прямого Тяготения (версия Ньютона) имеет определенный дефицит качественной аргументации по направлениям:.
1. Равновесие тела на орбите .
2. Знак минус перед формой 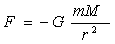 . (знак, не имеющий физической природы).
. (знак, не имеющий физической природы).
3. Равномерное распределение материи на макро уровне.
4. Возгонка хвоста кометы .
5 . Замороженный лунный прилив (вытянутая форма Луны).
6. Высота приливов.
7. Работа, совершаемая приливами.
8. Расширение Вселенной.
Из них официально признано (что явление физически не обеспечено):
1. Высота приливов
2 . Работа, совершаемая приливами.
3. Замороженный лунный прилив ( Явление могло бы иметь место при монолитности Луны.
В то же время официальная наука признает, что монолитность Луны – невозможна.)
Вся выше перечисленная проблематика убедительно разрешается по заявленной версии Комплексного Тяготения.
Решающим преимуществом версии Комплексного Тяготения – является наличие реального силового фактора обеспечивающего данные, наблюдаемые в природе физические явления.



 Подробнее о данной проблематике: По версии прямого притяжения, для тел связанных
Подробнее о данной проблематике: По версии прямого притяжения, для тел связанных 
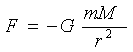 имеется два возможных сценария:
имеется два возможных сценария:
- либо находиться в лавинообразном процессе образования макротела,
- либо занимать место в пространстве согласно принципов взаимного силового равновесия.
Предположим, что тела в лавинообразном процессе не участвуют, тогда их положение в пространстве соответствует силовому равновесию и определяется только реальными физическими силами.


 Статический аспект взаиморасположения в пространстве для тел равной массы будет соответствовать состоянию, отображенному на рисунке №44 (равномерно заполненное пространство), а положение отдельно взятого тела будет соответствовать состоянию, отображенному на рисунке №45
Статический аспект взаиморасположения в пространстве для тел равной массы будет соответствовать состоянию, отображенному на рисунке №44 (равномерно заполненное пространство), а положение отдельно взятого тела будет соответствовать состоянию, отображенному на рисунке №45
 (поскольку при введении в схему расчетного тела большей массы, взаимное расположение остальных тел изменится).
(поскольку при введении в схему расчетного тела большей массы, взаимное расположение остальных тел изменится).
Вокруг каждого более массивного тела, образуется разряженная область, в физическом плане обеспеченная взаимным равенством сил.
Данная динамика сходится с наблюдениями (чем более массивным является скопление небесных объектов, тем значительнее разряженная область это скопление объектов содержащая (пример – галактики и окружающие их области.)
Из чего для системы отсчета связанной с Солнцем, расположение внешних тел (равной массы), будет силовым аналогом схемы отраженной на рис.№ 46:
, а для системы отсчета связанной с телом, аналогом схемы № 47:



 Из чего очевидно наличие разряженной области вокруг Солнца (схема № 48 и № 49), а так же очевидно, что данная область (как и на ранее приводимой схеме) - смещена относительно пробного тела. Из приведенной схемы наглядно видно, что если рассматривать материю, заключенную в сферу с центром, совпадающим с центром опытного тела - наблюдается изменение количества масс, для правой и левой половин, приведенного к сфере, комплекса удаленных объектов. Это и есть изменение положения тел относительно избранной системы отсчета.
Из чего очевидно наличие разряженной области вокруг Солнца (схема № 48 и № 49), а так же очевидно, что данная область (как и на ранее приводимой схеме) - смещена относительно пробного тела. Из приведенной схемы наглядно видно, что если рассматривать материю, заключенную в сферу с центром, совпадающим с центром опытного тела - наблюдается изменение количества масс, для правой и левой половин, приведенного к сфере, комплекса удаленных объектов. Это и есть изменение положения тел относительно избранной системы отсчета.
Таким образом, мы наглядно убедились, что данное физическое явление физически обосновано и действительно имеет место быть в природе.
 На данном этапе стоит отметить: Расположение тел определяется геометрией разряженной области, а само силовое взаимодействие в количественном плане определяется не разряженной областью, а конкретными массами.
На данном этапе стоит отметить: Расположение тел определяется геометрией разряженной области, а само силовое взаимодействие в количественном плане определяется не разряженной областью, а конкретными массами.
Следовательно, в расчете мы должны учитывать не разряженную область, а именно массы.
И из расчетного значения комплекса мы выводим не разряженную область, а линейное выражение конкретных масс.
 И если касательно области у нас может сложиться впечатление, что она окружает пробное тело, то ни одна из масс окружить тело не может, масса каждого тела находится относительно расчетного тела всегда с одной стороны (например, справа или слева в рамках телесного угла).
И если касательно области у нас может сложиться впечатление, что она окружает пробное тело, то ни одна из масс окружить тело не может, масса каждого тела находится относительно расчетного тела всегда с одной стороны (например, справа или слева в рамках телесного угла).
То есть в силовом плане расположение масс, характеризующих разряженную область и массы самого расчетного тела, всегда соответствует схеме, в которой расчетное тело находится на удалении и не проникает внутрь какой либо отдельной массы.



 Поскольку ситуацию с «разнокалиберными» телами довольно затруднительно анализировать приведем весь комплекс небесных тел к равномерной взвеси мелких тел равной массы (схема№50).
Поскольку ситуацию с «разнокалиберными» телами довольно затруднительно анализировать приведем весь комплекс небесных тел к равномерной взвеси мелких тел равной массы (схема№50).
Приведем к данному состоянию и Солнце
(Расчетное тело оставим в неизменном состоянии. Схема №51).
Динамика силовых взаимодействий в рамках условия взаимного равновесия приводит систему к однородному равномерному распределению тел в пространстве.
 Следует понимать, что данная схема хоть и наглядно представляет принципы распределения масс в пространстве, но в то же время для непосредственного определения сил данная схема должна быть видоизменена. Поскольку непосредственное воздействие фактически осуществляется не от «разнесенных» масс, а из вполне конкретных центров масс реальных тел.
Следует понимать, что данная схема хоть и наглядно представляет принципы распределения масс в пространстве, но в то же время для непосредственного определения сил данная схема должна быть видоизменена. Поскольку непосредственное воздействие фактически осуществляется не от «разнесенных» масс, а из вполне конкретных центров масс реальных тел.
 И в реальной ситуации между Солнцем и телом разнесенных откалиброванных масс нет, и нет возможности в них проникнуть. Де-факто массы находятся справа и слева на удалении. То есть в качестве векторной базы схема имеет вид, обозначенный на схеме №52 (с открытой зоной).
И в реальной ситуации между Солнцем и телом разнесенных откалиброванных масс нет, и нет возможности в них проникнуть. Де-факто массы находятся справа и слева на удалении. То есть в качестве векторной базы схема имеет вид, обозначенный на схеме №52 (с открытой зоной).
Рассмотрим количественное выражение данного реального физического явления.

 Перемещение разряженной области между поверхностями двух заданных концентрических сфер:
Перемещение разряженной области между поверхностями двух заданных концентрических сфер:

 При перемещении разряженной области между поверхностями двух концентрических сфер, изменяется объем конуса образованного телесным углом, следовательно, изменяется количество материи, заключенной между двумя сферическими поверхностями в рамках телесного угла обозначенного габаритами разряженной области (прямая геометрическая зависимость от телесного угла).
При перемещении разряженной области между поверхностями двух концентрических сфер, изменяется объем конуса образованного телесным углом, следовательно, изменяется количество материи, заключенной между двумя сферическими поверхностями в рамках телесного угла обозначенного габаритами разряженной области (прямая геометрическая зависимость от телесного угла).
При этом сами тела - ни куда не исчезли. Суммарно материи (масс в пространстве) осталось - ровно столько сколько было. А вот между поверхностями двух концентрических сфер, в рамках изменённого телесного угла - материи стало действительно меньше. В этом можно наглядно убедиться, сравнив объемы выделенных телесным углом областейна приведенных в тексте схемах Рис.№53 и №54.
На данном этапе стоит так же отметить следующее:


 Поскольку сфера* с равномерным распределением даёт ноль суммарного воздействия, то в дальнейшем расчете полные сферы - учитывать надобности нет. Их можно отбросить и учитывать только сферы* содержащие неравномерности.
Поскольку сфера* с равномерным распределением даёт ноль суммарного воздействия, то в дальнейшем расчете полные сферы - учитывать надобности нет. Их можно отбросить и учитывать только сферы* содержащие неравномерности.
Конечная расчетная схема, соответствует приведенной на рисунке № 55
Дополнительные пояснения: Для того чтобы привести комплекс удаленных объектов к сфере задействуется операция известная как: Центральная проекция на поверхность сферы (общий курс Пространственной Геометрии).
При данной операции положение всех точек (частных масс) проецируется на поверхность сферы заданного диаметра в направлении центра сферы (Рисунки № 56, №57, №58).

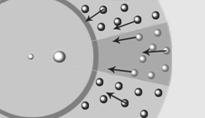

Рисунок № 56. Рисунок №57. Рисунок №58.

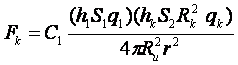
Сила как фактор, определяющий равновесие:
Силовое равновесие тела на орбите в рамках системы отсчета связанной с центрами масс (обоих тел), определено соотношением силы Тяготения и Центробежной силы.
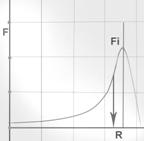
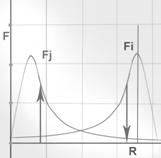
Рассмотрим графики изменения силы Тяготения и силы Центробежной от расстояния.
Для Центробежной силы график выглядит как 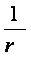 ,
,
а для тяготения как 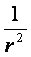
| R | 1/4 | 1/2 | |||
| F тягот. | 1/4 | 1/16 | |||
| F центр. | 1/2 | 1/4 |
 Точка пересечения графиков – точка равенства сил (точка силового равновесия /силовое состояние спутника на орбите).
Точка пересечения графиков – точка равенства сил (точка силового равновесия /силовое состояние спутника на орбите).
Силовое состояние спутника на орбите может быть устойчивым равновесием, а может быть неустойчивым равновесием (безразличное – не рассматриваем) и это изначально определяется не параметрами движения тела, а физическими условиями самой системы (приращением сил).
 Чтобы силовое состояние спутника было устойчивым равновесием – необходимо чтобы при единичном смещении возникали силы стремящиеся возвратить систему в состояние равновесия.
Чтобы силовое состояние спутника было устойчивым равновесием – необходимо чтобы при единичном смещении возникали силы стремящиеся возвратить систему в состояние равновесия.
Рассмотрим силы, приложенные к спутнику.
С единичным смещением запустим спутник на более низкую орбиту (масса - const, линейная скорость const).
По версии прямого притяжения сила Тяготения – увеличится.
Приращение силы Тяготения направлено на вывод тела из равновесия. Возникают силы стремящиеся вывести тело из состояние равновесия, что наглядно отслеживается на графике изменения силы от расстояния.
Далее: Сила, притягивающая тела находится в зависимости от расстояния между объектами (от 1/r^2,)
Увеличение расстояния между объектами, на одну линейную единицу приводит к возникновению силы 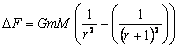
Уменьшение расстояния между объектами, на одну линейную единицу приводит к приращению силы 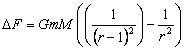
Единичное смещение расчетного тела (спутника) так же приводит и к изменению Центробежной силы..
Однако линейная скорость тела на каждый конкретный момент времени константа.
Кроме того расчетное приращение центробежной силы на единицу смещения значительно меньше, чем приращение силы тяготения.

 Из данных графиков однозначно следует, что если бы действительно наблюдаемая картина мира была построена на законе тяготения (по версии притяжения), то ни какой планетарности не было бы в принципе.
Из данных графиков однозначно следует, что если бы действительно наблюдаемая картина мира была построена на законе тяготения (по версии притяжения), то ни какой планетарности не было бы в принципе.
(приращение силы направлено строго в противоположную сторону от требуемого ). Тело на таких приращениях силы удерживаться в планетарном режиме не может, и при любом отличном от нуля смещении должно покинуть орбиту (причем не только исходную, но и все остальные теоретически предполагаемые).
То есть по факту - по версии прямого тяготения, удержать тело на орбите – не возможно. Нет сил обеспечивающих данное явление. Более того, приращения силы делают планетарность по версии прямого притяжения невозможной в принципе.
Это ещё одно доказательство верности комплексной версии тяготения и неверности трактовки Ньютона.
По версии комплексного отталкивания как раз таки имеется реальная сила обеспечивающая равновесие (см. график). Частные силы отталкивания между телами, как раз дают частные приращения силы, направленные на поддержание устойчивого равновесия в том виде, в каком мы его наблюдаем в природе:
И если бы не количественно превышающее отталкивание от комплекса
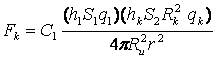
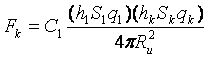

 мы бы в теории могли иметь безразличное равновесие (как в модели «отталкивающейся Вселенной», разлетающейся в незамкнутое пространство с нулевой плотностью).
мы бы в теории могли иметь безразличное равновесие (как в модели «отталкивающейся Вселенной», разлетающейся в незамкнутое пространство с нулевой плотностью).
Далее:В примере с двумя плоскостями мы имеем для сил притяжения – неустойчивое равновесие, а для сил отталкивания – устойчивое равновесие (причем в самой «замкнутой» форме – безразличное равновесие). В данной схеме приложение сил не приводит к выводу тела из равновесия.

 В других же геометрических условиях (планетарная схема) силовая замкнутость отсутствует. Факторов влияющих на это несколько. Опишем их подробнее: Мы хоть и считаем тяготение как взаимодействие центров масс, но фактически тяготение находится в зависимости от телесного угла. При приближении тела, телесный угол увеличивается (часть масс разносится в стороны, и в дальнейшем следует продвижения в центр Земли). Разнос масс (зависимость от телесного угла) – это не большой, но размыкающий фактор (график скругляется). Кроме того - в реальной модели (где плоскостей нет) имеется ощутимая разница между внешним и внутренним (от Солнца) воздействием (этот фактор зависит от реальных расстояний).
В других же геометрических условиях (планетарная схема) силовая замкнутость отсутствует. Факторов влияющих на это несколько. Опишем их подробнее: Мы хоть и считаем тяготение как взаимодействие центров масс, но фактически тяготение находится в зависимости от телесного угла. При приближении тела, телесный угол увеличивается (часть масс разносится в стороны, и в дальнейшем следует продвижения в центр Земли). Разнос масс (зависимость от телесного угла) – это не большой, но размыкающий фактор (график скругляется). Кроме того - в реальной модели (где плоскостей нет) имеется ощутимая разница между внешним и внутренним (от Солнца) воздействием (этот фактор зависит от реальных расстояний).

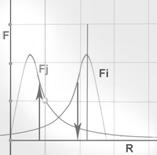
Если взаимодействующие плоскости разводить то замыкающий фактор ослабевает, поскольку увеличивается свободная зона. Фактический разнос масс во вселенной – несопоставимо больше чем в схеме с условно приближенными магнитами. Дополнительным размыкающим фактором является Центробежная сила, которая целиком зависит от скорости данного тела. А поскольку скорость тела (спутника) мы изначально можем задавать весьма в широких пределах, то и значение центробежной силы у нас изменяется соответственно. Следовательно и значение результирующей силы приложенной к спутнику может находиться тоже в широких пределах. В схеме с двумя плоскостями данный силовой фактор (Центробежная сила) в принципе - отсутствует.
Второй фактор. При приближении к одной плоскости у нас ослабевает воздействие от второй.
В объемной же (планетарной) схеме ситуация радикально отлична.
При приближении к частному центру масс воздействие от комплекса не уменьшается, а количественно растет Малые и другие отклонения в большинстве случаев как раз и возникают под действием внешних сил.Любое единичное изменение расстояния между центрами масс (отклонение первого типа) приводит (согласно Закона Всемирного Тяготения) к приращению силы dF. Это приращение силы по версии прямого притяжения, не компенсируется соответствующим противоположно направленным, уравновешивающим приращением других сил. Следовательно, данное приращение силы, вызванное отклонением первого типа направлено на вывод системы из равновесия.
Из чего следует однозначный вывод, что планетарные системы на силах притяжения не соответствуют определениям Закона Сохранения Энергии. Следовательно, такие планетарные системы физически невозможны.
Рассмотрим некоторые моменты подробнее:
Введем понятие Гравитационный магнит - условно принятая плоскость, бесконечной площади, оказывающая постоянное, равномерное гравитационное воздействие заданной величины. Приведем поверхность условной звезды к плоскости, и пустим вдоль этой плоскости тело (планету). Уравновесим систему равномерным приложением противоположно направленного воздействия, для этого используем второй соответственно расположенный магнит. Изолируем систему от внешнего воздействия.
 Зададим гравитационным магнитам силы притяжения.Две параллельные плоскости, и планета.
Зададим гравитационным магнитам силы притяжения.Две параллельные плоскости, и планета.
Снизу вверх:
-магнит (звезда) ,
-планета ,
-магнит ( уравновешивающий )
Тело движется поступательно (между магнитов). Любое воздействие (не направленное параллельно плоскости магнита) выводит систему из равновесия.
(приращение силы направлено на вывод из равновесия)
От любого приложения силы - получается смещение рассматриваемого тела, изменяется расстояние до магнита, при изменении расстояния изменяется сила. Процесс ускоряющийся. Такое равновесие - возможно только в изолированной системе. То есть практически не возможно.
Рассмотрим другую версию: ( так же для сил притяжения) . Введем комплекс удаленных объектов. Снизу вверх :-магнит №1 - левого сектора приведенного к плоскости комплекса удаленных объектов , -магнит №2 (звезда) , -планета ,
-магнит №3 (уравновешивающий),
-магнит №4 - правого сектора комплекса удаленных объектов.
Тело движется поступательно, направленно. Любое воздействие (не направленное параллельно плоскости магнита) выводит систему из равновесия. От любого приложения силы - получается смещение, смещение изменяет расстояние до магнита, при изменении расстояния изменяется сила. и т. д. процесс ускоряющийся.
Вывод: Равновесие - возможно только в идеальной системе. То есть практически не возможно.
Состояние устойчивого равновесия не является возможным для тела находящегося под воздействием равномерно приложенных сил притяжения.
Посмотрим как та же схема работает при отталкивании:
Снизу вверх:
магнит №1 - левого сектора, приведенного к плоскости комплекса удаленных объектов ,
магнит №2 (звезда) , планета ,
магнит №3 ( уравновешивающий ) ,
магнит №4 - правого сектора комплекса удаленных объектов.
Тело движется поступательно, направленно. Направленное воздействие не выводит систему из равновесия. От приложения силы - получается смещение, на встречу смещению мы наблюдаем приращение силы со стороны магнита.
Данная схема соответствует определениям Закона Сохранения Энергии и является единственно возможной из приведенных схем.
Общий вывод по теме:
Принятая на веру, широко распространенная точка зрения: что составляющие сил гравитации, сами являются именно силами притяжения , не соответствует, определениям Закона Сохранения Энергии, в силу чего является физически неверной.
Одним из условий равновесия тела на орбите , является наличие математически выражаемых границ существования* ( то есть допуска) в каждой отдельно взятой точке орбиты (имеется в виду границы от ноля до некого значения). Для орбиты как для совокупности точек равновесия, такие границы могут возникнуть только от постоянного воздействия направленных сил. Применительно к версии гравитация отталкивания мы указанным силовым воздействием, располагаем. С внешней стороны орбиты располагаем в виде сил отталкивания от комплекса удаленных объектов, с внутренней стороны орбиты в виде воздействия сил отталкивания от самого тела. Следовательно, границы существования не равны нолю а имеют какое то значение. В случае с гравитацией притяжения, ввиду отсутствия направленных сил, границы любой орбиты изначально равны нолю. Значит допуск для этого состояния равновесия тоже равен нолю. Границы существования такого явления равны нолю. Значит это явление в принципе не возможно.
Вывод: планетарные системы на силах притяжения невозможны в принципе.
.
 Эксперименты:
Эксперименты:
Эксперимент по подтверждению невозможности бесконтактных форм равновесия ( даже неорбитального ) на силах притяжения.
На вертикальном нейтральном стержне с зазором, обеспечивающим свободный ход, размещаем два магнита ( возможны две версии полярной ориентации).
Закрепляя поочередно магнит на стержне и меняя его ориентацию, мы можем отследить взаимодействие по версии притяжения, и по версии отталкивания.
Для отталкивания: Магнит №1 закрепляем внизу стержня, магнит №2 опускаем сверху.
При достижении определенного приближения, магнит «зависает» (в поле) и дальше не продвигается.
Вывод: устойчивое равновесие на силах отталкивания достижимо.
Эффект нагляден, экспериментально достижим.
Далее: Эксперимент для притяжения:
 Магнит № 1 закрепляем вверху стержня, магнит №2 поднимаем на гибкой связи.
Магнит № 1 закрепляем вверху стержня, магнит №2 поднимаем на гибкой связи.
При достижении определенного приближения, магнит либо устремляется к другому магниту, либо падает вниз и повисает на гибкой связи.
Вывод: устойчивое равновесие на силах притяжения не достижимо.
Чему есть и другое практическое подтверждение - за все время существования человеческой цивилизации ни одну планетарную систему на подтвержденных силах притяжении ни кто не построил.
 Эксперимент на устойчивость орбиты при неустойчивом равновесии:
Эксперимент на устойчивость орбиты при неустойчивом равновесии:
Эксперимент: Устанавливаеммагнит на горизонтальную плоскость, чертим на плоскости устойчивую орбиту.
Для стального шарика массой М, согласно заданного радиуса, рассчитываем требуемую скорость. Запускаем шарик по орбите.
Проводим эксперимент со всеми возможными скоростями, со всеми прикидками на трение.
Орбитальное движение не наблюдается даже в кратковременной форме.
Дата добавления: 2016-09-06; просмотров: 2178;











