Определение реакций в опорах

Вектор силы полного давления зуба шестерни на зуб ведомого колеса F_n направлен по нормали к образующей поверхности зуба [6, с. 306]. Для косозубой передачи этот вектор (рис.11) представляет собой диагональ параллелепипеда, сторонами которого являются три составляющие силы по трем взаимно перпендикулярным направлениям: F_a, F_r и F_t. В прямозубой передаче осевая сила отсутствует, и сила давления на колесо – это диагональ параллелограмма со сторонами F_r и F_t.

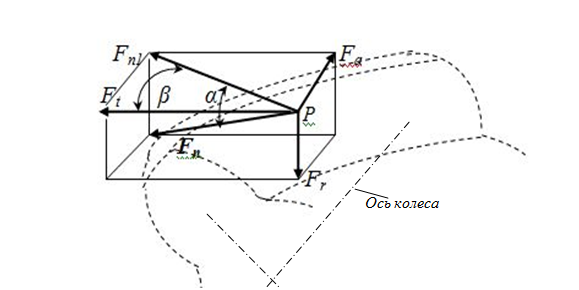
Рис. 11. Силы, действующие в зацеплении косозубой передачи.

Окружная сила: F_t = 2Т/d,

где Т – крутящий момент, d – диаметр делительной окружности

зубчатого колеса.

Осевая сила F_a = F_t· tgβ .

Радиальная сила F_r = F_t· tgα /cosβ.

Определение реакций опор цилиндрической косозубой передачи рассмотрим на примере быстроходного вала. Для этого необходимо построить расчетную схему, как показано на рис. 12.

Реакции находим, пользуясь обычными уравнениями статического равновесия, известными из курса теоретической механики. Изобразив систему координат, реакции раскладываем на составляющие в горизонтальной плоскости XOZ и в вертикальной плоскости УOZ.

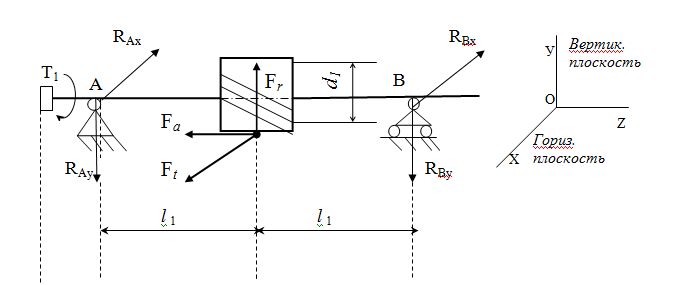
Рис. 12.Расчетная схема для определения реакций в опорах

Уравнения равновесия в горизонтальной плоскости

ΣM_B = -R_AX ∙ 2l₁ + F_t ∙ l₁ = 0; R_AX = F_t / 2.

ΣX = -R_AX - R_BX + F_t= 0; R_BX = F_t - R_AX = F_t / 2.

Уравнения равновесия в вертикальной плоскости

ΣM_B = R_Ау∙2l₁ -F_а∙ d₁ / 2 - F_r / l₁ = 0; R_Ау= F_r / 2 + F_а ∙ d₁ / 4l₁.

ΣM_А = - R_Ву∙2l₁ -F_а ∙ d₁ / 2 + F_r / l₁ = 0; R_Ву= F_r / 2 - F_а∙ d₁ / 4l₁ .

Равнодействующие реакции находим, как геометрическую сумму:

;

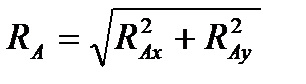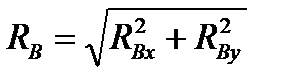
В нашем примере (опоры расположены симметрично) в горизонтальной плоскости реакции равны, а в вертикальной – более нагружена опора А, в сторону которой направлена осевая сила. При несимметричном расположении опор от полюса зацепления могут быть другие соотношения.