Построение эпюр изгибающих и крутящих моментов. Определение эквивалентного момента.

<3 4 5 6 789 >

Под действием внешних сил, реакций в опорах и моментах в сечениях вала возникают внутренние крутящие и изгибающие моменты. Таким образом, вал испытывает сложную деформацию – изгиб с кручением. Как известно из курса «Сопротивление материалов» расчет вала на прочность можно выполнять на основании принципа независимости действия сил. В этом случае необходимо определить напряжения от каждой силы или момента, после чего рассчитать эквивалентный момент, согласно третьей теории прочности [6, с.275-276].

;

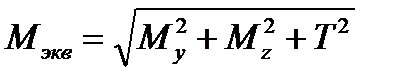
М_у – изгибающий момент в горизонтальной плоскости;

М_Z - изгибающий момент в вертикальной плоскости;

Т – крутящий момент.

Далее можно вычислить эквивалентное напряжение для круглых валов

Ϭ_экв= М_экв/ W ≤ [Ϭ],

где W – осевой момент сопротивления.

[Ϭ] – допускаемое напряжение на изгиб.

При этом расчет ведут как для изгиба (без кручения), но не по изгибающему, а по эквивалентному моменту.

Для определения эквивалентного момента строим эпюры внутренних крутящих моментов, а также эпюры изгибающих моментов в горизонтальной и вертикальной плоскости (рис.13).

На входном участке вала от полумуфты до полюса зацепления действует постоянный вращающий момент Т₁. При зацеплении шестерни с зубчатым колесом крутящий момент передается на колесо, и далее посредством шпоночного соединения – на тихоходный вал. Поэтому внутренний крутящий момент на участке от полюса зацепления до опоры В равен нулю.

Изгибающий момент в горизонтальной плоскости:

- на участке от опоры А до точки зацепления (слева от сечения) эпюра изгибающего момента строится по уравнению:

М_ИГ= R_A_х∙ z ; где 0 ≤ z ≤ l₁

При z = 0 М_ИГ = 0; при z = l₁М_ИГ= F_t ∙ l₁ / 2.

-на участке от опоры В до точки зацепления (справа от сечения):

М_ИГ= R_Вх∙ z ; где 0 ≤ z ≤ l₁

При z = 0 М_ИГ = 0; при z = l₁М_ИГ= F_t ∙ l₁ / 2.

Изгибающий момент в вертикальной плоскости:

- на участке от опоры А до точки зацепления (слева от сечения)

М_ИВ= R_A_у∙ z ; где 0 ≤ z ≤ l₁

При z = 0 М_ИВ = 0; при z = l₁М_ИВ= F_r ∙ l₁/ 2 + F_а∙ d₁/ 4 .

- на участке от опоры В до точки зацепления (справа от сечения):

М_ИВ= R_Ву∙ z ; где 0 ≤ z ≤ l₁

При z = 0 М_ИВ =0; при z = l₁М_ИВ= F_r ∙ l₁/ 2 - F_а∙ d₁/ 4 .

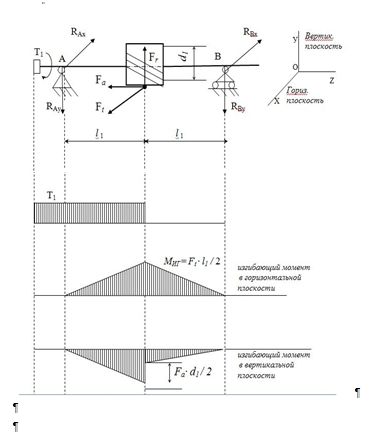
Рис.13. Построение эпюр крутящего и изгибающих моментов

<3 4 5 6 789 >

Дата добавления: 2021-06-28; просмотров: 575;

Поиск по сайту

Узнать еще