Общее уравнение плоскости и уравнение в отрезках

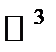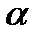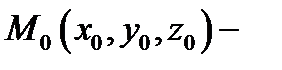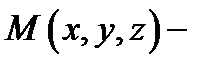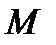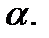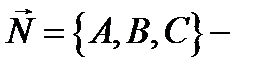Пусть в пространстве задана плоскость и пусть фиксированная точка, а произвольная (текущая) точка этой плоскости. Посмотрим, какому уравнению будет подчинена произвольная точка плоскости Пусть вектор нормали к плоскости 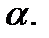Так как 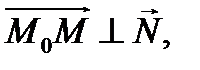то скалярное произведение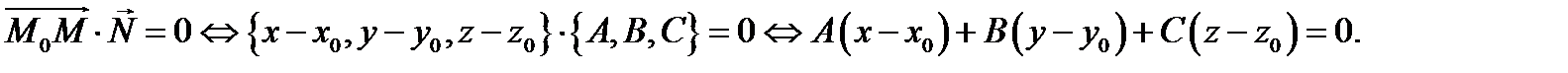

Мы получили

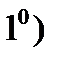уравнение плоскости, проходящей через фиксированную точку 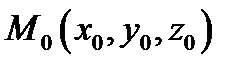с вектором нормали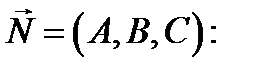 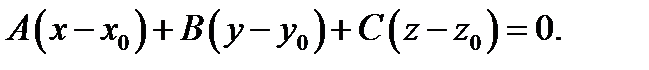(1)

Раскроем в (1) скобки и обозначим 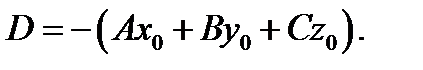Получим

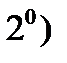общее уравнение плоскости:
Имеет место следующее очевидное утверждение.

Теорема 1.Любое линейное уравнение (2) задаёт в пространстве 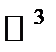плоскость с вектором нормали 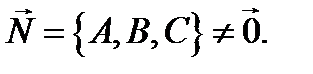И обратно: любая плоскость в 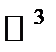описывается линейным уравнением (2).

Если числа 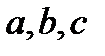не равны нулю, то уравнение 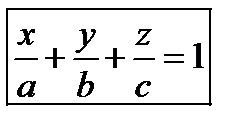называют “уравнением плоскости в отрезках” (впредь кавычки будем опускать). При этом 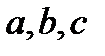являются величинами (с учётом знака) отрезков, отсекаемых плоскостью от осей 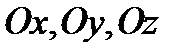соответст-венно. Эта плоскость проходит через точки 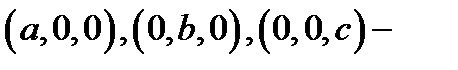факт, удобный при изображении этой плоскости в пространстве. Из общего уравнения (2) плоскости легко получить ее уравнение в отрезках: 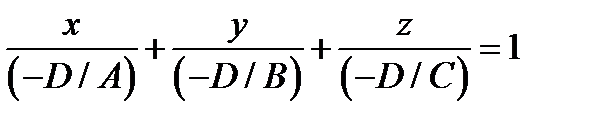(если, конечно, числа, записанные в знаменателях, существуют).