Скалярное, векторное и смешанное произведение векторов
Дадим определения этих произведений в краткой форме.
а) Скалярное произведение векторов 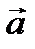 и
и 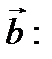
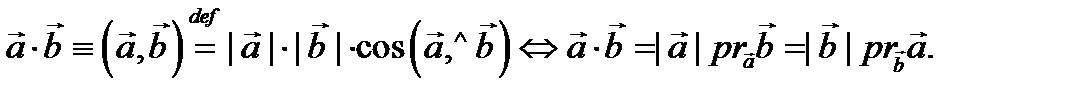
б) Векторное произведение векторов 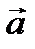 и
и 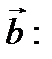
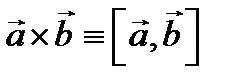 - есть вектор
- есть вектор 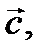 удовлетворяющий требованиям:
удовлетворяющий требованиям:
1) 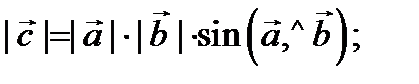 2)
2) 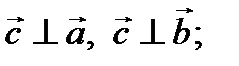 3)тройка
3)тройка 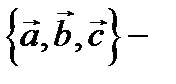 правая, т.е. кратчайший поворот от вектора
правая, т.е. кратчайший поворот от вектора 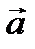 к вектору
к вектору 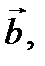 имеющих общее начало, виден из конца вектора
имеющих общее начало, виден из конца вектора 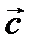 (с тем же началом) совершающимся против часовой стрелки.
(с тем же началом) совершающимся против часовой стрелки.
в) Смешанное произведение векторов 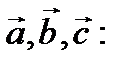
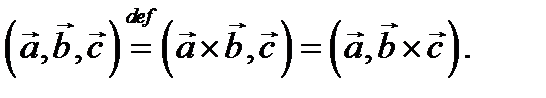
Введенные операции умножения над векторами обладают свойствами ассоциативности и дистрибутивности. Свойство коммутативности верно лишь для скалярного произведения. При перемене мест сомножителей в векторном произведении изменяется знак (антикоммутативность): 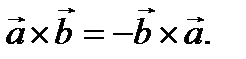 То же может произойти и в смешанном произведении. Например,
То же может произойти и в смешанном произведении. Например, 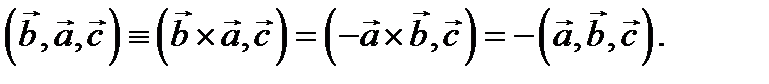 Учитывая свойство антикоммутативности векторного произведения, можно обращаться с введенными произведениями векторов как с обычным произведением чисел. Например,
Учитывая свойство антикоммутативности векторного произведения, можно обращаться с введенными произведениями векторов как с обычным произведением чисел. Например,
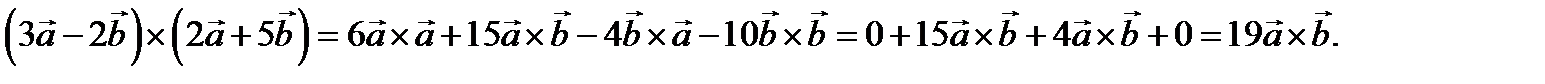
Здесь учтено, что векторное произведение коллинеарных векторов равно нулю (здесь и далее вместо 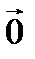 пишем просто 0).
пишем просто 0).
Имеют место следующие утверждения, вытекающие из а), б) и с).
 Скалярное произведение
Скалярное произведение 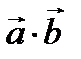 векторов
векторов 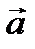 и
и 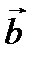 равно нулю
равно нулю 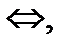 когда векторы
когда векторы 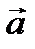 и
и 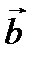 ортогональны друг другу.
ортогональны друг другу.
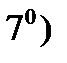 Векторное произведение
Векторное произведение 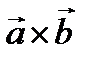 равно нулю
равно нулю 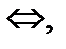 когда векторы
когда векторы 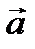 и
и 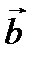 коллинеарны.
коллинеарны.
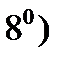 Смешанное произведение
Смешанное произведение 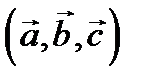 равно нулю
равно нулю 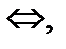 когда векторы
когда векторы 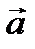 ,
, 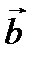 и
и 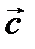 компланарны (т.е. все они либо лежат в одной плоскости, либо находятся в параллельных плоскостях).
компланарны (т.е. все они либо лежат в одной плоскости, либо находятся в параллельных плоскостях).
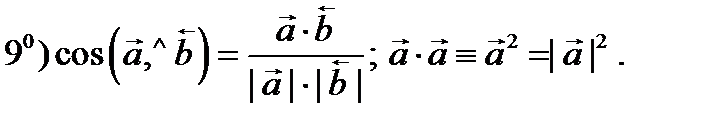
Геометрический смысл: а) модуль 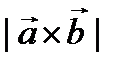 векторного произведения численно равен площади параллелограмма, построенного на векторах
векторного произведения численно равен площади параллелограмма, построенного на векторах 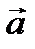 и
и 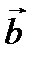 ; б) модуль
; б) модуль 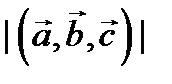 смешанного произведения равен объёму параллелепипеда, построенного на векторах
смешанного произведения равен объёму параллелепипеда, построенного на векторах 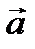 ,
, 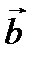 и
и 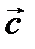 .
.
Прежде чем дать формулы для вычисления произведений векторов в координатной форме, введем понятие определителей второго и третьего порядков:
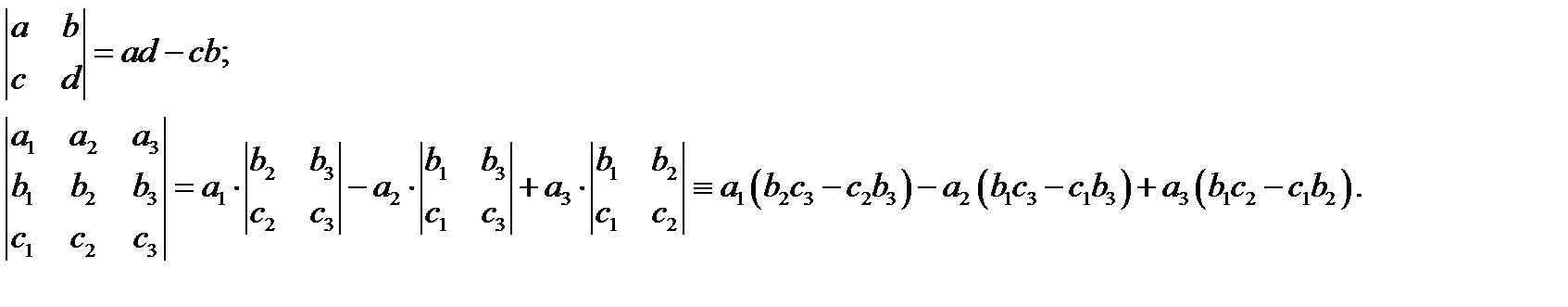
Теорема 4.Если векторы 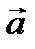 и
и 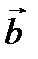 заданы своими координатами
заданы своими координатами 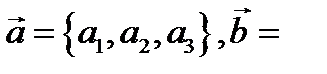
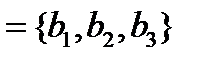 в базисе
в базисе 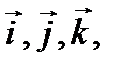 то имеют место формулы:
то имеют место формулы:
а) 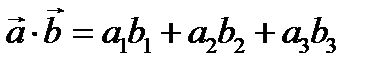 (скалярное произведение;)
(скалярное произведение;)
б) 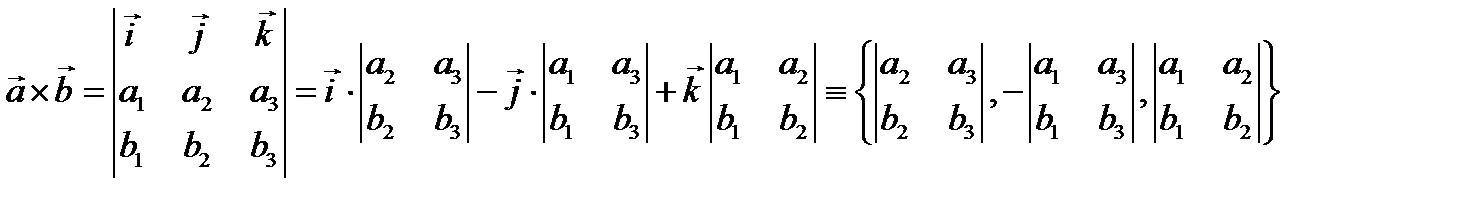 (векторное произведение);
(векторное произведение);
в) 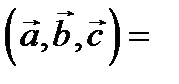
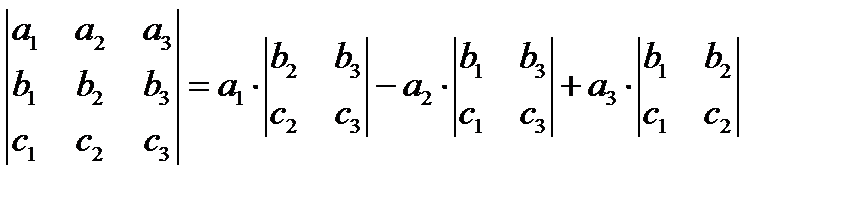 (смешанное произведение).
(смешанное произведение).
Доказательствопроведем лишь для скалярного произведения. Имеем
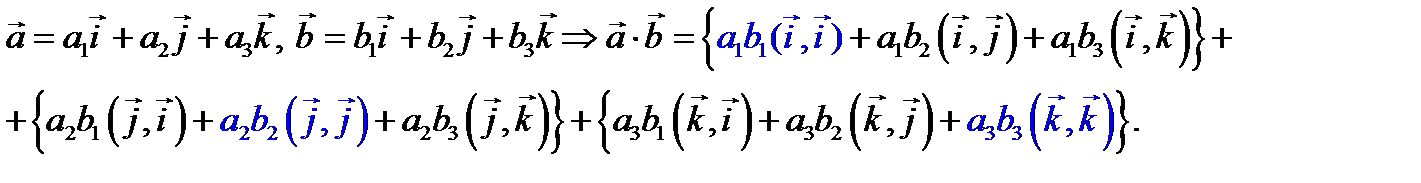
Учитывая, что векторы 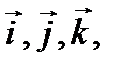 попарно ортогональны, получаем, что в этой сумме только слагаемые с множителями
попарно ортогональны, получаем, что в этой сумме только слагаемые с множителями 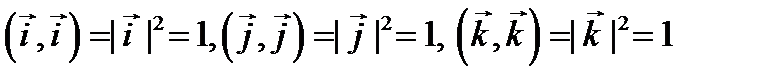 не равны нулю; все другие слагаемые равны нулю. Значит, имеет место формула
не равны нулю; все другие слагаемые равны нулю. Значит, имеет место формула 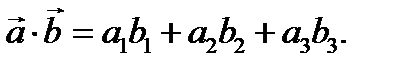 Теорема доказана.
Теорема доказана.
Лекция 2. Плоскость и прямая в пространстве
Сначала заметим, что множество всех точек 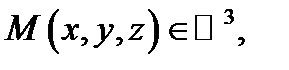 удовлетворяющих уравнению
удовлетворяющих уравнению 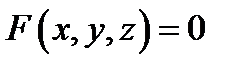 (если его можно разрешить относительно хотя бы одной из переменных
(если его можно разрешить относительно хотя бы одной из переменных 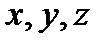 ) является уравнением некоторой поверхности
) является уравнением некоторой поверхности  . Это означает, что любая точка
. Это означает, что любая точка
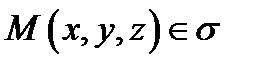 удовлетворяет уравнению
удовлетворяет уравнению 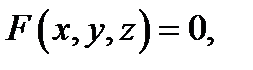 и, напротив, если
и, напротив, если 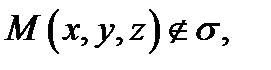 то она не удовлетворяет этому уравнению.
то она не удовлетворяет этому уравнению.
Дата добавления: 2016-06-05; просмотров: 2454;











