Взаимное пересечение геометрических фигур.
Две геометрические фигуры, пересекаясь, дают общий элемент:
- Прямая с прямой - точку (а Ç b Þ К).
- Прямая с плоскостью - точку (а Ç S Þ К).
- Прямая с поверхностью - одну или несколько точек (а Ç D Þ К, М ...).
- Плоскость с плоскостью - прямую линию (S Ç Г Þ а).
- Плоскость с поверхностью - плоскую кривую или плоскую ломаную (S Ç D Þ m).
- Поверхность с поверхностью - пространственную кривую или несколько пространственных кривых, которые, в свою очередь, могут состоять из плоских кривых или плоских ломаных (D Ç L Þ m).
Из всего многообразия этих задач выделяются две общие задачи, которые называют главными позиционными задачами:
Первая главная позиционная задача (1 ГПЗ) - пересечение линии с поверхностью (первые
три задачи).
Вторая главная позиционная задача (2 ГПЗ) - взаимное пересечение двух поверхностей
(4, 5 и 6 задачи).
При этом следует помнить, что плоскость - это частный случай поверхности, поэтому условимся пересечение плоскостей или плоскости с поверхностью относить ко 2 ГПЗ.
При решении 2 ГПЗ сначала необходимо выяснить, что будет являться общим элементом у двух пересекающихся поверхностей. Чаще всего бывает следующее:
а) Пересекаются два многогранника - общий элемент есть пространственная ломаная линия, состоящая из отдельных звеньев (каждое звено - прямая линия), как результат пересечения граней многогранников; звенья между собой соединены в точках А, В, С ..., которые представляют собой точки пересечения рёбер первого многогранника с гранями второго и наоборот (рис. 3-1).
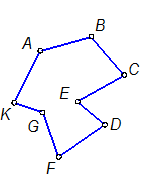
Рис. 3-1
б) Пересекаются многогранник с кривой поверхностью (например, тор с пирамидой). Общий элемент - пространственная кривая линия, состоящая из отдельных звеньев. Каждое звено есть результат пересечения граней многогранника с кривой поверхностью (звенья m, n, k ...- есть плоские кривые). Звенья между собой соединены в точках А, В, С, D, которые представляют собой результат пересечения рёбер многогранника с кривой поверхностью (рис. 3-2а).
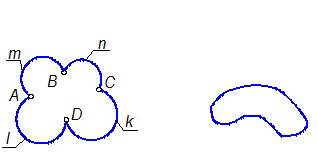
| Рис. 3-2а | Рис. 3-2б |
в) Пересекаются две кривые поверхности (например, сфера с конусом). Общий элемент - пространственная кривая линия (рис. 3-2б).
Далее необходимо определить количество общих элементов пересекающихся поверхностей. Определяется оно в зависимости от характера пересечения поверхностей.
Дата добавления: 2016-05-31; просмотров: 2538;











