Взаимное пересечение двух плоскостей

Первый способ построения линии пересечения двух плоскостей состоит в следующем. Вводят вспомогательную плоскость Г (рис. 4.10), строят линии пересечения вспомогательной плоскости с двумя заданными и при пересечении построенных линий находят общую точку К двух заданных плоскостей. Для нахождения второй общей точки К' построение повторяют с помощью второй вспомогательной плоскости Г'.

В качестве вспомогательных плоскостей обычно берут плоскости частного положения – плоскости уровня относительно плоскостей проекции (горизонтальные, фронтальные) или проецирующие (перпендикулярные к плоскостям).

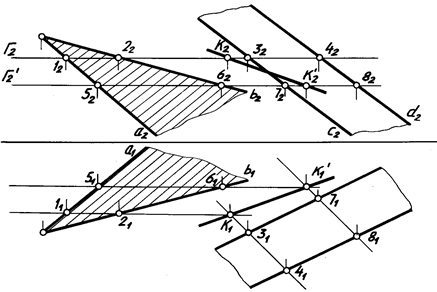
Рис. 4.10

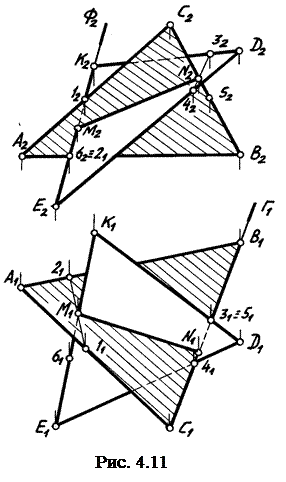Для построения линии пересечения двух плоскостей можно использовать точки пересечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью. Для этого точку пересечения прямой с плоскостью строят, как это указано в подразд. 4.5, т. е. через заданную прямую проводят вспомогательную проецирующую плоскость, строят пересечения вспомогательной и заданной плоскостей, в пересечении построенной линии с заданной прямой отмечают искомую точку. Определим линию пересечения двух треугольников вторым из указанных выше способов (рис. 4.11). Точка пересечения прямой КЕ с плоскостью треугольника АВС – М – найдена с помощью вспомогательной фронтально проецирующей плоскости Ф, фронтальный след которой совпадает с К₂Е₂. Вспомогательная плоскость пересекается с плоскостью треугольника АВС по линии 1-2. Пересечение горизонтальных проекций этой линии и прямой КЕ – М₁ – является горизонтальной проекцией первой точки линии пересечения заданных плоскостей, ее фронтальная проекция построена по принадлежности прямой КЕ.

Аналогичным способом найдена и точка N, которая является точкой пересечения прямой ВС с плоскостью треугольника DЕК. Разница только в том, что в качестве вспомогательной взята горизонтально проецирующая плос-
кость Г, горизонтальный след которой совпадает с В₁С₁. Эта плоскость пересекает треугольник DЕК по линии 3-4. Пересечение фронтальных проекций этой линии и прямой ВС – точка N₂ – является фронтальной проекцией искомой точки, ее горизонтальная проекция находится по принадлежности прямой ВС.

Видимость геометрических элементов на комплексном чертеже определяется с помощью конкурирующих точек, проекции которых на какую-либо плоскость проекции совпадают. Из двух горизонтально конкурирующих точек на П₁ видна будет та, у которой больше высота, т. е. координата Z, а из двух фронтально конкурирующих видима та, у которой больше координата Y.

Видимость плоскостей треугольников на горизонтальной плоскости проекций определена с помощью горизонтально конкурирующих точек 3 и 5, а на фронтальной – с помощью фронтально конкурирующих точек 2 и 6. Точка 3 расположена выше точки 5 (координата Z у нее больше), поэтому она будет видимой на П₁. Так как эта точка принадлежит прямой KD, то и прямая будет видимой.

На фронтальной проекции видимой будет прямая KE, так как принадлежащая ей точка 6 видимая – она расположена ближе к наблюдателю (координата Y у нее больше), чем конкурирующая с ней точка 2.

5. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА

Преобразования комплексного чертежа необходимы для решения позиционных и метрических задач. Преобразования осуществляются двумя принципиальными способами: заменой плоскостей проекций или изменением положения предмета относительно плоскостей проекций. Здесь будет рассмотрен только первый способ преобразования.

Все преобразования комплексного чертежа можно свести к решению четырех основных задач:

1) прямая общего положения преобразуется на чертеже в прямую уровня;

2) прямая уровня преобразуется в проецирующую прямую;

3) плоскость общего положения преобразуется в плоскость проеци-
рующую;

4) плоскость проецирующая преобразуется в плоскость уровня.