Кинематика материальной точки
Физика – наука об окружающем нас мире. Физика – наука опытная. Ее цель и задачи состоят в том, чтобы понять всю природу, как разные проявления одной совокупности физических явлений и происходящих в ней процессов. Открыть законы, стоящие за этими процессами и объединить отдельные явления природы, предварительно разъединив их для подробного изучения.
Физика, как наука, возникла благодаря, прежде всего, трудам греческого философа Аристотеля (384 – 322 г.г. до н.э.). Аристотель собрал и систематизировал огромный естественнонаучный материал предшественников (как говорят, он владел всеми знаниями той эпохи) и сам осуществил ряд глубоких наблюдений. Несмотря на то, что в его взглядах на строение окружающего нас мира было много заблуждений, они просуществовали около 16 веков, т.к. во многом совпадали с догматами церкви. Следующий шаг в развитии физики и, прежде всего механики, сделали итальянский ученый Галилео Галилей (1564 – 1642 г.г.) и англичанин Исаак Ньютон (1643 – 1727 г.г.). Именно они заложили основы так называемой классической механики, которую мы будем изучать в течение всего первого семестра.
1. Движение в пространстве. Способы задания положения тел в пространстве (векторный способ, координатный способ, «естественный» способ).
Механика – раздел физики, в котором изучается механическое движение, т.е. изменение положения тел в пространстве относительно других с течением времени. Механика, в свою очередь, чисто формально, разделяется на кинематику и динамику. В кинематике изучается механическое движение без выяснения причины того или иного характера движения (состояние покоя, равномерного прямолинейного движения или движение с ускорением).
Как ни странно, механика не может точно описать ни один реальный физический процесс, происходящий в окружающем нас мире. Дело в том, в ходе каждого реального процесса происходит множество тесно связанных друг с другом явлений, которые не поддаются математическому описанию (составлению формул). Выход состоит в том, чтобы пользоваться моделями, поддающимися математическому описанию. От модели совсем не требуют внешнего сходства с описываемым объектом, достаточно, чтобы совпадали их свойства. Такой моделью в механике является материальная точка.
Материальная точка это тело, размерами которого можно пренебречь в условиях данной задачи. Например, в одних задачах Землю можно считать материальной точкой, а в других – нельзя.
Основными физическими понятиями раздела «Кинематика материальной точки» являются: механическое движение, траектория, система отсчета, путь и перемещение, средняя и мгновенная скорость, равномерное прямолинейное движение, ускорение.
Механическое движение – изменение положения тел в пространстве относительно других тел. Рассмотрим для начала способы задания положения тел в пространстве (идет речь о материальных точках).
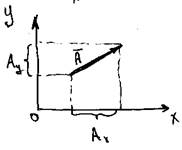
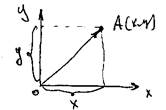
Обратимся к рис.1(а,б).
 | |||
 | |||
а) б)
Рис.1
На рис.1 (а) показаны декартовы координаты х, у точки А на плоскости. Здесь же приведен радиус-вектор этой точки А. Видно, что координаты радиус-вектора точки А совпадают с ее декартовыми координатами. На рис. 1 (б) приведены проекции на оси координат произвольного вектора 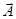 (проведенного не из начала координат).
(проведенного не из начала координат).
Любой вектор 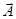 удобно представлять с помощью единичного вектора некоторого произвольного направления. На рис.2 представлено некоторое произвольное направление и указан единичный вектор этого направления
удобно представлять с помощью единичного вектора некоторого произвольного направления. На рис.2 представлено некоторое произвольное направление и указан единичный вектор этого направления 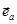 .
.
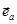

Рис.2
Тогда любой вектор 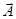 этого направления можем записать в следующем виде:
этого направления можем записать в следующем виде:
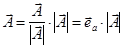 .
.
Радиус – вектор удобно разлагать по осям координат с помощью единичных векторов- ортов. Рассмотрим рис.3.
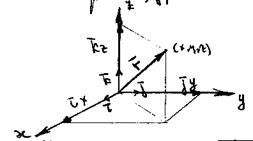
Рис.3
Здесь 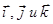 - единичные векторы (орты) декартовой системы координат в пространстве. Тогда разложение радиус-вектора
- единичные векторы (орты) декартовой системы координат в пространстве. Тогда разложение радиус-вектора 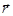 по ортам выглядит следующим образом:
по ортам выглядит следующим образом:
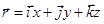 .
.
Рассмотрим теперь способы задания положения точки в пространстве.
1. Векторный способ.
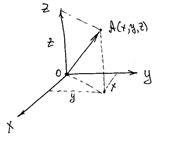
В этом способе следует задать начало отсчета – точку О. Тогда положение некоторой точки А относительно этого начала отсчета можно задать с помощью радиус-вектора, как показано на рис.4. Таким образом, задается зависимость 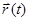 .
.
 |
Рис.4
Геометрическое место точек концов радиус-вектора называется траекторией. Введем вектор перемещения, как 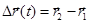 . Назовем средней скоростью движения величину:
. Назовем средней скоростью движения величину:
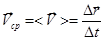 .
.
Видно, что направление средней скорости совпадает с направлением вектора перемещения.
Если уменьшать интервал времени 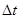 , то в пределе получим мгновенную скорость следующим образом:
, то в пределе получим мгновенную скорость следующим образом:
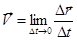 .
.
Мгновенная скорость представляет собой производную по времени от радиус-вектора.
Замечание.
Отметим, что в общем случае 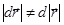 . Например, в случае движения точки по окружности с постоянной по модулю скоростью
. Например, в случае движения точки по окружности с постоянной по модулю скоростью 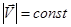 ясно, что,
ясно, что, 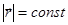 и, следовательно, d
и, следовательно, d 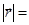 0. С другой стороны,
0. С другой стороны, 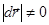 , т.к. вектор все время изменяет свое направление.
, т.к. вектор все время изменяет свое направление.
При изменении скорости возникает ускорение, которое можно определить следующим образом: 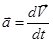 , или с помощью разложения по ортам декартовой системы координат:
, или с помощью разложения по ортам декартовой системы координат:
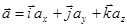 .
.
Таким образом, зная зависимость 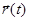 , можно вычислить скорость и ускорение тела в любой момент времени.
, можно вычислить скорость и ускорение тела в любой момент времени.
Существует и обратная задача – зная ускорение в виде зависимости 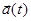 , найти скорость и перемещение тела. Для решения этой задачи воспользуемся интегральным исчислением. По определению
, найти скорость и перемещение тела. Для решения этой задачи воспользуемся интегральным исчислением. По определению 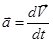 и правую часть этого выражения можно рассматривать, как производную скорости по времени, с другой стороны, ее можно рассматривать как отношение двух бесконечно малых величин – дифференциала (бесконечно малого приращения) скорости dV и дифференциала (бесконечно малого приращения) времени dt. Тогда следует очевидное:
и правую часть этого выражения можно рассматривать, как производную скорости по времени, с другой стороны, ее можно рассматривать как отношение двух бесконечно малых величин – дифференциала (бесконечно малого приращения) скорости dV и дифференциала (бесконечно малого приращения) времени dt. Тогда следует очевидное:
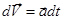 .
.
Отсюда можно записать при V0 =0:
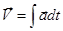 .
.
Найдем теперь перемещение тела, используя определение мгновенной скорости:
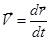 .
.
Тогда можем записать 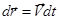 , или окончательно
, или окончательно 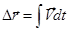 .
.
Поскольку для модуля мгновенной скорости можем записать 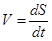 , где S – путь, пройденный телом вдоль траектории, то величину этого пути можно найти с помощью следующего выражения:
, где S – путь, пройденный телом вдоль траектории, то величину этого пути можно найти с помощью следующего выражения:
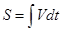 .
.
2. Координатный способ.
 Задавим начало отсчета точку О, и свяжем с ней декартову систему координат в пространстве (рис. 5).
Задавим начало отсчета точку О, и свяжем с ней декартову систему координат в пространстве (рис. 5).
Рис. 5
Тогда, зная зависимости координат частицы от времени, можно рассчитать ее скорость и ускорение в любой другой момент времени следующим образом:
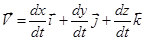 и
и 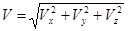
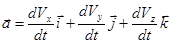 и
и 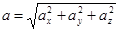 .
.
Также это дает возможность рассчитать направление векторов скорости и ускорения по формулам:
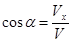 ,
, 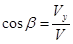 ,
, 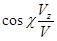 .
.
3. «Естественный» способ.
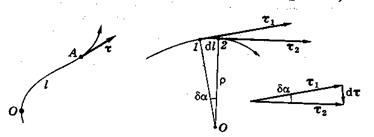 Это способ задания положения точки в пространстве с помощью параметров траектории. Рассмотрим рис.6.
Это способ задания положения точки в пространстве с помощью параметров траектории. Рассмотрим рис.6.
Рис. 6
Точка О задает начало отсчета для движения вдоль траектории точки А. Измеряя длину траектории l от начала О до положения точки в данный момент времени, можно задавать положение точки в любой момент времени.
Введем единичный вектор касательной к траектории в данной точке 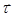 . При движении вдоль траектории произвольной формы меняется направление этого вектора
. При движении вдоль траектории произвольной формы меняется направление этого вектора 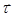 , следовательно, он изменяется во времени.
, следовательно, он изменяется во времени.
Поскольку, по определению, мгновенная скорость является производной перемещения по времени, а вектор перемещения совпадает с хордой, соединяющей два последовательных положения тела А и В, то направление вектора скорости в данной точке совпадает с предельным положение хорды, т.е. с касательной (см. рис. 7).
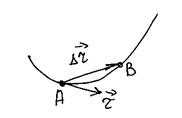 |
Рис. 7
Можем теперь написать 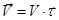 . Здесь V- модуль вектора скорости. Более точной является запись
. Здесь V- модуль вектора скорости. Более точной является запись 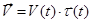 .
.
Найдем мгновенное ускорение точки по формуле:
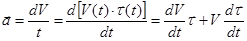 .
.
Чисто формально ( с точки зрения математики) ускорение разделилось на две составляющие его части. Попытаемся найти физический смысл каждой составляющей. Первое слагаемое 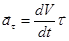 назовем тангенциальным, поскольку его направление совпадает с направлением касательной к траектории движения точки. Выясним более подробно смысл величины
назовем тангенциальным, поскольку его направление совпадает с направлением касательной к траектории движения точки. Выясним более подробно смысл величины 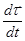 , являющейся производной единичного вектора касательной по времени.
, являющейся производной единичного вектора касательной по времени.
Производная единичного вектора по времени.
По определению производной 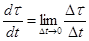 . С другой стороны,
. С другой стороны, 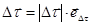 , вектор
, вектор
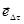 представляет собой направление вектора
представляет собой направление вектора 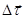 . Теоретически доказывается, вектор
. Теоретически доказывается, вектор
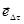 направлен перпендикулярно касательной к траектории в данной точке, а
направлен перпендикулярно касательной к траектории в данной точке, а 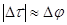 (угол поворота вектора
(угол поворота вектора 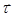 ). Следовательно, можем написать:
). Следовательно, можем написать:
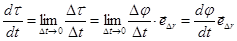 .
.
По определению при вращательном движении по окружности угловая скорость 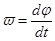 , следовательно:
, следовательно:
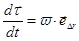 .
.
Поскольку существует связь модуля угловой и линейной скорости ( 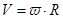 ), то можем записать:
), то можем записать:
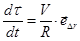 .
.
Теперь для полного ускорения можем записать следующую формулу:
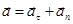 .
.
Здесь 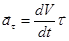 - тангенциальное ускорение, направленное по касательной к траектории в данной точке. Оно определяет изменение модуля скорости.
- тангенциальное ускорение, направленное по касательной к траектории в данной точке. Оно определяет изменение модуля скорости.
Другая составляющая полного ускорения 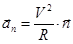 , где
, где 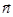 - единичный вектор нормали к касательной в данной точке траектории (см. рис. 8).
- единичный вектор нормали к касательной в данной точке траектории (см. рис. 8).
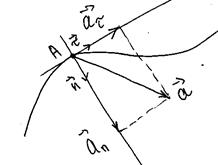 |
Рис. 8
Полное ускорение теперь записывается в виде:
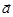 =
= 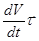 +
+ 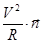 .
.
Дата добавления: 2018-11-26; просмотров: 644;











