Структурные формулы механизмов.

Существуют общие закономерности в структуре (строении) самых различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул механизмов.

Для пространственных механизмов в настоящее время наиболее распространена формула Малышева, вывод которой произ­водится следующим образом.

Пусть в механизме, имеющем m звеньев (включая, стойку), 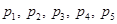- число одно-, двух-, трех-, четырех- и пятиподвижных пар. Число подвижных звеньев обозначим 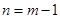. Если бы все подвижные звенья были свободными телами, общее число степеней свободы было бы равно 6n. Однако каждая одноподвижная пара V класса накладывает на относительное движение звеньев, образующих пару, 5 связей, каждая двухподвижная пара IV класса - 4 связи и т. д. Следовательно, общее число степеней свободы, равное шести, будет уменьшено на величину

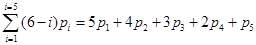
где 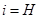- подвижность кинематической пары, 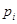- число пар, подвижность которых равна i. В общее число наложенных связей может войти некоторое число q избыточных (повторных) связей, которые дублируют другие связи, не уменьшая подвиж­ности механизма, а только обращая его в статически неопредели­мую систему [12]. Поэтому число степеней свободы пространствен­ного механизма, равное числу степеней свободы его подвижной кинематической цепи относительно стойки, определяется по следую­щей формуле Малышева:

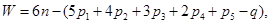
или в краткой записи

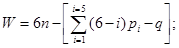(2.2)

при 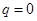механизм – статически определимая система, при 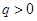- статически неопределимая система.

В общем случае решение уравнения (2.2) - трудная задача, поскольку неизвестны W и q; имеющиеся способы решений сложны и не рассматриваются в данной лекции. Однако в частном случае, если W, равное числу обобщенных координат механизма, найдено из геометрических соображений, из этой формулы можно найти число избыточных связей (см. Решетов Л. Н. Конструирование рациональных механизмов. М., 1972)

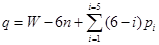(2.3)

и решить вопрос о статической определимости механизма; или же, зная, что механизм статически определимый, найти (или прове­рить) W.

Важно заметить, что в структурные формулы не входят размеры звеньев, поэтому при структурном анализе механизмов можно предполагать их любыми (в некоторых пределах). Если избыточных связей нет ( 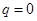), сборка механизма происходит без деформиро­вания звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися [12] . Если избыточные связи есть ( 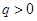), то сборка механизма и движение его звеньев становятся возможными только при деформировании последних.

Для плоских механизмов без избыточных связей структурная формула носит имя П. Л. Чебышева, впервые предложив­шего её в 1869 году для рычажных механизмов с вращательными парами и одной степенью свободы. В настоящее время формула Чебышева распространяется на любые плоские механизмы и выво­дится с учетом избыточных связей следующим образом

Пусть в плоском механизме, имеющем т звеньев (включая стойку), 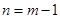-число подвижных звеньев, 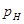- число низших пар и 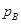- число высших пар. Если бы все подвижные звенья были свободными телами, совершающими плоское движение, общее число степеней свободы было бы равно Зn. Однако каждая низшая пара накладывает на относительное движение звеньев, образующих пару, две связи, оставляя одну степень свободы, а каждая высшая пара накладывает одну связь, оставляя 2 степени свободы.

В число наложенных связей может войти некоторое число 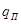избыточных (повторных) связей, устранение которых не увеличива­ет подвижности механизма. Следовательно, число степеней свободы плоского механизма, т. е. число степеней свободы его подвижной кинематической цепи относительно стойки, определяется по следую­щей формуле Чебышева:

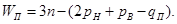(2.4)

Если 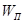известно, отсюда можно найти число избыточных связей

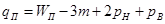(2.5)

Индекс «п» напоминает о том, что речь идет об идеально плос­ком механизме, или точнее о его плоской схеме, поскольку за счет неточностей изготовления плоский механизм в какой-то мере явля­ется пространственным.

По формулам (2.2)-(2.5) проводят структурный анализ имею­щихся механизмов и синтез структурных схем новых механизмов.