Определение безразмерных температурных полей в детали

При исследовании закономерностей формирования поверхностного слоя деталей в процессе их механической обработки весьма актуальным является определение температур, как на самой поверхности детали, так и по ее глубине. Основным источником теплоты при различных видах обработки – лезвийной, алмазно-абразивной, отделочно-упрочняющей является зона обработки, размеры которой существенно меньше размеров обрабатываемой детали.

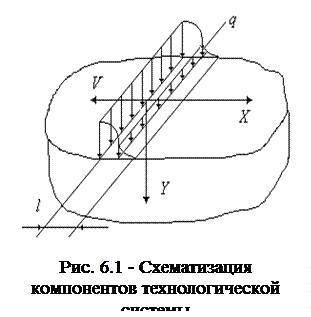В связи с этим, независимо от метода обработки, при схематизации компонентов технологической системы, представленной на рис.6.1 деталь рассматривается как полубесконечное тело. Источник теплоты, возникающий на поверхности заготовки в результате взаимодействия с инструментом, рассматривается как быстродвижущийся полосовой шириной l, определяемой условиями контакта инструмента с деталью. Мощность источника теплоты определяется скоростью его перемещения V и силой P, действующей в направлении перемещения источника в зоне обработки: W=PV.

Доля теплоты, поступающая в деталь:

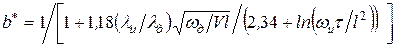, (6.1)

где l_и , l_д , w_и , w_д – коэффициенты теплопроводности и температуропроводности инструмента и детали соответственно, t - время действия источника.

Температурное поле в детали для полосового быстродвижущегося источника описывается аналитическим выражением:

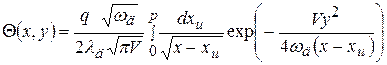, (6.2)

где x_u – абсцисса импульса теплоты; x, y – абсцисса и ордината точки, для которой рассчитывается температура; p= l, если x³ l, p= x, если x< l.

Для исследования температурного поля в детали целесообразно перейти к безразмерным величинам ( ; ; ):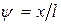

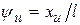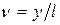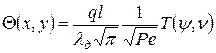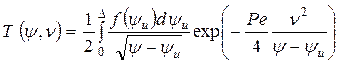; , (6.3)

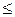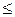где Pe = Vl/ω_д - критерий Пекле; Т(ψ,ν) - безразмерное распределение температур; D - верхний предел интеграла: D = y при 0 y 1 и D = 1 при y > 1;f(y_и) - закон распределения плотности теплового потока.

Распределения безразмерных температур на поверхности детали Т(y) (координата n = 0) и по глубине детали Т(n) (координата y = 1) имеют вид:

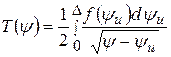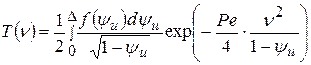; . (6.4)

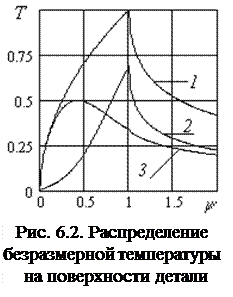
Графики распределения безразмерной температуры на поверхности заготовки при n = 0 для различных законов распределения представлены на рис.6.2. Установлены координаты точек на поверхности детали, имеющих максимальную температуру: для равномерного закона распределения плотности теплового потока (кривая 1) с функцией распределения 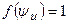безразмерная функцияимеет наибольшее значение T_max(1,0)=1 при y=1 и n=0; для нормального несимметричного закона распределения плотности теплового потока (кривая 2) с функцией распределения 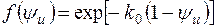, безразмерная функцияимеет наибольшее значение T_max(1,0)=0,685 при y=1 и n=0; для нормального несимметричного закона распределения плотности теплового потока (кривая 3) с функцией распределения 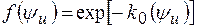, безразмерная функцияимеет наибольшее значение T_max(0.5,0)=0.5 при y=0,5 и n= 0.

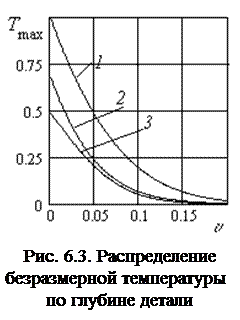
Распределение максимальной безразмерной температуры по глубине детали T_max(y,n), при значениях y, обеспечивающих этот максимум, представлено на рис.6.3. Графики свидетельствуют о том, что температура по глубине поверхности достаточно быстро убывает, причем независимо от закона распределения уже при n=0,2 становиться практически равной 0.