Излучательные и безызлучательные переходы.

Рассмотрим монохроматическую электромагнитную волну на частоте v, взаимодействующую с полупроводником. Если hυ>>E_G, то эта волна будет поглощаться полупроводником. Ради простоты мы не будем вдаваться в квантовомеханический рас­чет процесса поглощения. В действительности результаты по­добных расчетов редко используются на практике. Мы лишь от­метим, что в случае прямого перехода должен сохраняться пол­ный импульс:

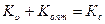, (4.3)

где К_с и К_υ— волновые векторы электрона соответственно в ва­лентной зоне и зоне проводимости, а К_опт — волновой вектор па­дающей электромагнитной волны. Однако в оптическом диапазоне К_опт = 2π/λ ~ 10⁵ см-¹, в то время как К_с и К_υ имеют порядок 10⁸ см-¹. Поэтому можно принять приближение К_опт = 0 и записать (4.3) в виде:

К_с = К_υ, (4.4)

так что переходы должны происходить между начальным и ко­нечным состояниями с одним и тем же вектором К. Условие (4.4) называют условием сохранения импульса кристалла. Заметим, что у непрямозонного полупроводника минимум зоны проводимости имеет место при К, отличном от того, которое соответствует максимуму валентной зоны. В этом случае переход между указанными двумя состоя­ниями может произойти, если в нем будет участвовать фонон решетки, чтобы скомпенсировать несохранение импульса кри­сталла. Однако непрямые переходы гораздо слабее, и это явля­ется основной причиной того, что лазерную генерацию никогда не удавалось наблюдать в непрямозонных полупроводниках, та­ких, как кремний.

Будучи заброшенным в зону проводимости, электрон релаксирует путем безызлучательных переходов (взаимодействуя с фононами решетки) на дно этой зоны. Не давно было показано, что этот внутризонный переход происходит в течение очень короткого времени(<100 фс). В то же время дырка, оставшаяся в валентной зоне, релаксирует за очень короткое время к верхушке валентной зоны. В этой точке электрон может рекомбинировать с дыркой либо излучательным, либо безызлучательным путем. Время жизни для межзонных переходов составляет около 1 нс, т.е. много больше времени жизни внутризонных переходов. Как известно, безызлучательные межзонные переходы происходят на глубоких ловушках, причем соответствующая энергия передается фонону решетки или свободным носителям. В полупроводниках, используемых в качестве активных сред лазеров, излучательная релаксация преобладает над безызлучательной, и квантовый выход люминесценции может достигать 80 % или даже больших значений.

1.1.3 Условие усиления электромагнитной волны
в полупроводнике

Рассмотрим неравновесное состояние полупроводника, когда из валентной зоны в зону проводимости переведено много электронов (например, за счет быстрого оптического воздействия). Поскольку внутризонные переходы имеют значительно большую скорость (t »10^-11 ¸10^-13 с), чем межзонные (t»10^-8¸10^-9с) внутри каждой зоны быстро устанавливается термодинамическое равновесие, хотя полупроводник как целое и не находится в термодинамическом равновесии (рис.4.1,б). Поэтому можно по отдельности говорить о вероятностях заполнения для валентной зоны f_u и для зоны проводимости f_c, которые даются выражениями, имеющими тот же вид, что и формула (4.2), а именно:

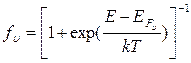, (4.3.а)

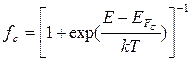. (4.3.б)

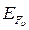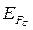где и - энергии так называемых квазиуровней Ферми соответственно для валентной зоны и зоны проводимости.

В процессе перехода полупроводника из неравновесного состояния в равновесное происходит излучательная рекомбинация, т.е. переходы электронов из зоны проводимости в валентную зону сопровождаются выделением избыточной энергии в виде квантов света. Если за счет накачки создать инверсию населенностей на переходах излучательной рекомбинации, то возможно получение эффекта квантового усиления в полупроводнике.

Определим теперь условие создания инверсии в полупроводнике. Вследствие образования квантов света в процессе излучательной рекомбинации в полупроводнике, скорость заполнения фотонами частоты n некоторой моды объема V равна: V×dN_n /dt = (A+BN_n ), (4.4)

где N_n - число фотонов в моде. Первый член в правой части соответствует спонтанной излучательной рекомбинации, а второй – разности вынужденного испускания и поглощения квантов света. При температуре Т равновесное заполнение моды фотонами подчиняется статистике Бозе - Эйнштейна, т.е.: N_n = 2/[exp(hn/kT) –1]. (4.5)

Так как при равновесии dNn /dt = 0, то из выражения (4.4) находим:

А/В = - N_n (4.6)

Рассмотрим теперь переходы между уровнем с энергией Е₂ в зоне проводимости и уровнем с энергией Е₁ в валентной зоне полупроводника. Скорость излучательной рекомбинации на выбранном переходе пропорциональна произведению концентрации электронов на уровне Е₂ и дырок на уровне Е₁. Как известно, вероятность нахождения электрона в состоянии с энергией Е задается распределением Ферми - Дирака (4.2), а вероятность нахождения на уровне Е дырки равна вероятности того, что этот уровень не занят электроном, т.е. величине:

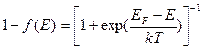. (4.7)

Следовательно, вероятность спонтанной рекомбинации пропорциональна произведению вероятности нахождения электронов на уровне Е₂ и вероятности нахождения дырки на уровне Е₁, т.е.:

А = А₀ f(Е₂)[1 - f(Е₁)], (4.8)

где А₀ – коэффициент пропорциональности.

Таким же образом, вероятность вынужденного излучения будет пропорциональна произведению вероятности заполнения верхнего уровня и вероятности того, что нижний уровень будет свободным, в то время как вероятность поглощения будет пропорциональна вероятности заполнения нижнего уровня и вероятности того, что верхний уровень окажется свободным. Тогда величина В, определяющая в (4.4) разность скоростей вынужденного испускания и поглощения квантов света, составляет:

B = B₂f(Е₂) [1 - f(Е₁)] - B₁f(Е₁) [1 - f(Е₂)], (4.9)

где В₁ и В₂ - коэффициенты пропорциональности. Подставляя (4.8) и (4.9) в (4.6) и с учетом равновесных распределений (4.2) и (4.5) имеем:

exp (hn/kT) –1 = 2В₂/А₀{B₁/B₂exp[(E₂-E₁)/kT] –1}. (4.10)

Так как фотоны с энергией hn возникают при переходах между уровнями Е₂ и Е₁, то hn=(Е₂ - Е₁). Тогда уравнение (4.10) всегда верно, если В₁ = В₂ = А₀/2 и выражение (4.9) примет вид:

B = А₀/2 [f(Е₂) - f(Е₁)]. (4.11)

Разность скоростей вынужденного испускания и поглощения квантов света на переходе Е₂→ Е₁, как видно из выражения (4.11), будет положительна при выполнении условия: [f(Е₂) - f(Е₁)]>0. (4.12)

Выбранные нами уровни Е₂ и Е₁ находятся, соответственно, в зоне проводимости и валентной зоне, которые имеют отдельные квазиравновесные распределения (4.3). Следовательно, функции распределения f(Е₂) и f(Е₁) можно представить в виде:

f(Е₂)=[1+exp(E₂ – E_Fc )/kT]^-1, f(Е₁)=[1+exp(E₁ – E_Fu )/kT]^-1, (4.13)

Подставляя эти выражения в (4.12) получим:

(E_Fc -E_Fu )> (Е₂ - Е₁) = hn . (4.14)

Также заметим, что энергия излучаемого фотона должна, очевидно, быть больше ширины запрещенной зоны Е_g , т. е. справедливо неравенство: Е_g = (Е_c - Е_u )< hn<(E_Fc - E_Fu ). (4.15)

Отсюда окончательно получим, что разность скоростей вынужденного испускания и поглощения квантов света на переходе Е₂→Е₁ будет положительна при выполнении условия: (E_Fc - E_Fu )>Е_g. (4.16)

Таким образом, инверсия между уровнями Е₂ и Е₁ достигается, если в результате воздействия на полупроводниковый образец излучения накачки квазиуровни Ферми окажутся внутри соответствующих разрешенных зон полупроводника.