Дифференциальное уравнение теплопроводности

Математическое описание температурных полей в компонентах технологических систем, как и в любых других твердых телах, выполняется с помощью дифференциального уравнения теплопроводности.

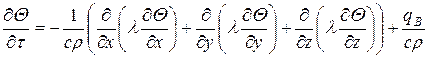, (1.11)

где с—массовая теплоемкость, Дж/(кг·°С); r - плотность вещества, кг/м³; q_B – интенсивность внутренних источников теплоты

В последнем выражении мы не выносим величину l за скобки, поскольку в общем случае коэффициент теплопроводности вещества зависит от температуры. Выражение (1.11) представляет собой дифференциальное уравнение теплопроводности, которое описывает в самом общем виде температурное поле, возникающее в твердом теле под действием внешних и внутренних источников теплоты.

Рассмотрим некоторые частные случаи. Если нагрев твердого тела осуществляется только внешними источниками теплоты, то q_B= 0 и уравнение (1.11) упрощается. Дальнейшее упрощение можно получить, если положить, что коэффициент теплопроводности не зависит от температуры:

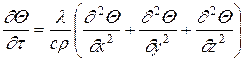, (1.12)

где l/cr=w— коэффициент температуропроводности данного вещества, м²/с.

Коэффициент температуропроводности w, как и коэффициент теплопроводности l, является физической характеристикой материала. С увеличением w возрастает скорость изменения температуры в данной точке твердого тела. Выражение (1.12) представляет собой линейное дифференциальное уравнение в частных производных второго порядка, выражение (1.11) является нелинейным дифференциальным уравнением, поскольку здесь учтена зависимость коэффициента теплопроводности от температуры.

Двух- или одномерное температурное поле:

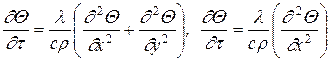. (1.13)

Дифференциальное уравнение теплопроводности можно применить к условиям стационарного теплообмена. Тогда во всех предыдущих формулах, относящихся к этому уравнению, следует принять дθ/дτ = 0. Например, для трехмерной, двух- и одномерной задач:

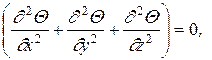
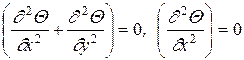. (1.14)

Лекция 2. Схематизация компонентов технологических систем