Определение перемещений, вызванных изменением температуры в статически определимых системах

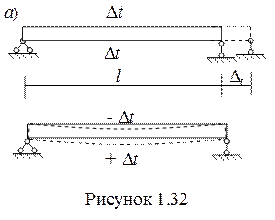
При равномерном нагревании прямолинейного стержня он удлиняется без осевых напряжений. Абсолютное удлинение составит

D_t = a∙l∙Dt,

где: a - температурный коэффициент линейного расширения,

Dt – приращение температуры.

При неравномерном нагреве такого стержня он искривляется без возникновения напряжений изгиба. Если температурное воздействие постоянно по длине стержня, искривление его аналогично деформации при чистом изгибе. Ниже будет рассмотрен такой случай.

Пусть стержень имеет прямоугольное сечение. Тогда нейтральная линия находится на середине высоты сечении h, и испытывает внешнее температурное воздействие, когда t₁ < t₂ (рисунок 1.33) .

Введем следующее допущение – по высоте стержня температура изменяется по линейному закону. Температура центрального волокна

t_ср = (t₁ + t₂)/2.

Разность температур крайних волокон обозначим

Dt = t₁ - t₂.

Тогда деформации элементарного участка стержня ds составят:

среднее удлинение

Dds =( t₁ads + t₂ads)/2 = t_срads, (а)

поворот сечения

dj = tgdj =( t₁ads - t₂ads)/h = (Dt a ds)/ h. (б)

Будем считать температурное воздействие на стержень первым (грузовым) состоянием. Второе состояние - единичное. Тогда возможная работа единичной силы, приложенной в сечении k, на температурном перемещении будет

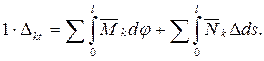. (в)

В связи с отсутствием сдвигов, отсутствует и интеграл, содержащий поперечную силу Q.

Подставим (а) и (б) в (в). В результате

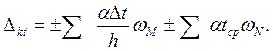(1.3)

где w_M иw_N – площади единичных эпюр M_k и N_k. Знак в формуле (1.3) принимается в зависимости от направления деформаций при воздействии температуры и единичного усилия (при совпадении направления деформаций знак «+»).

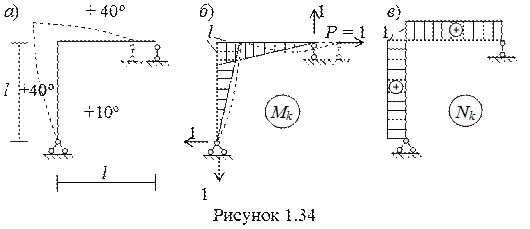
Пример 1,4. Определить горизонтальное смещение подвижной опоры рамы, показанной на рисунке 1.34, при изменении наружной температуры. Высота сечения элементов рамы h = l/10.

При повышении наружной температуры стойка и ригель будут выпучиваться наружу и права опора переместится влево.

Создаем единичное состояние (рисунок 1.34, б), прикладывая единичную силу по направлению искомого перемещения, и строим единичные эпюры M_k и N_k. Используем формулу (1.3), для чего найдем

w_M = l²/2 + l²/2 = l², w_N =1∙ l + 1∙ l = 2l.

Параметры температурного воздействия t_ср = (t₁ + t₂)/2 = 25º, Dt = t₁ - t₂ = 30º.

Вычисляем перемещение правой опоры

D_kt = a∙25∙2l - a∙30∙l²/(l/10) = 50al - 300al = - 250al.

Первый (положительный) член правой части выражает влияние удлинения оси системы, второй – влияние искривлений. Очевидно, что влиянием температурного удлинения стержня пренебрегать нельзя, поскольку оно составляет для данной задачи 16,7% от перемещений, вызванных искривлением.