Примеры расчета методом сил

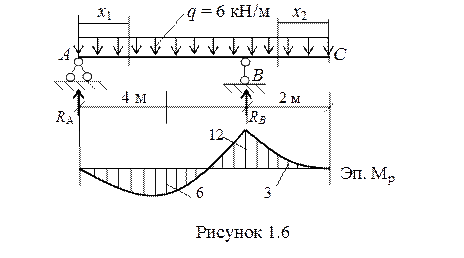
Пример 1.1 Определить, как изменится НДС шарнирно опертой с консолью балки постоянного сечения (EI = const), нагруженной распределенной нагрузкой q = 6 кН/м при установке в сечении «С» дополнительной опоры (рисунок 1.6).

Решение:

1 Проводим расчет статически определимой шарнирно опертой с консолью балки. Балка имеет два участка. Записываем на каждом участке выражения для изгибающих моментов и строим эпюру М.

Определяем опорные реакции.

Sm_В = 0. R_A×4 - q×6×1 = 0; R_A = 9 кН.

Sm_A = 0. R_B×4 - q×6×3 = 0; R_B = 27 кН.

Проверка: Sy = 0; R_A + R_B - q× 6 = 0

Записываем выражения для моментов.

1-й участок, 0 ≤ х₁ ≤ 4 м,

М₁ = R_A×x₁ - q×x₁²/2; М_х=0 = 0;

М_х=2 =18- 6×2 = 6 кНм; М_х=4 = 36 – 6×8 = - 12 кНм.

2-й участок, 0 ≤ х₂ ≤ 2 м,

М₁ = - q×x₂²/2; М_х=0 = 0;

М_х=1 =- 6×(1/2) = - 3 кНм; М_х=2 = – 12 кНм.

Строим эпюру М (рис. 1.6).

2 Проводим расчет этой же балки, но имеющей дополнительную опору в т С. (рисунок. 1.7 а). Балка стала один раз статически неопределима.

2.1 Выбираем основную систему, отбросив лишнюю связь (рисунок 1.7, б). При таком выборе основной системы построенная выше эпюра моментов может быть использована как грузовая эпюра для дальнейшего расчета.

2.2 Записываем каноническое уравнение для системы с одной степенью свободы

Х₁ δ₁₁ + Δ_1Р = 0.

2.3 Строим эпюру 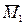и перемножив ее саму на себя, находим δ₁₁.

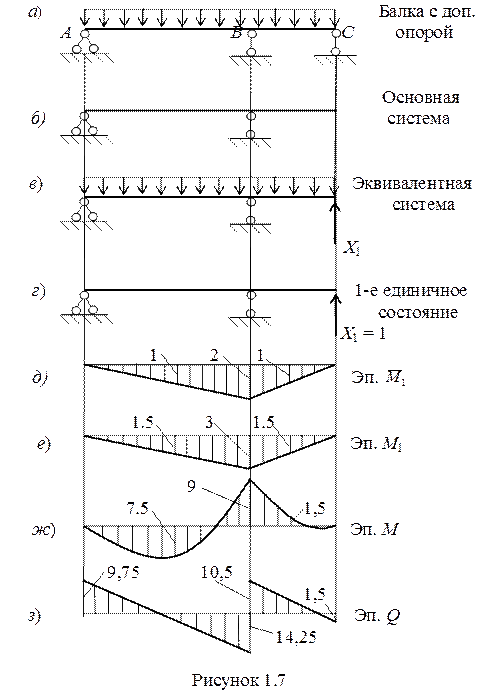
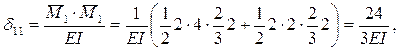
2.4. Вычисляем свободный член канонического уравнения

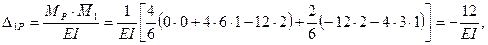
2.5. Записываем и решаем каноническое уравнение:

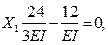
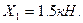
2.6. Строим эпюру М₁, как: М₁ = 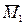×Х₁ (рис. 1.7, е)и, далее, строим результирующую эпюру М, в виде суммы М = М₁ + М_Р (рис. 1.7, ж).

2.7. Делаем кинематическую проверку, перемножая результирующую эпюру М на единичную.

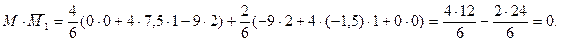
Проверка выполняется.

2.8 Вычисляем поперечные силы путем графического дифференцирования эпюры М.

Левый участок: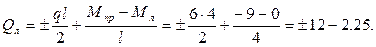

Q_л = 9,75 кН, Q_пр = -14,25 кН.

Правый участок: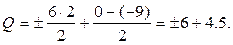

Q_л = 10,5 кН, Q_пр = -1,5 кН.

2.9 Делаем статическую проверку (рис. 1.8), получив значения реакций из эпюры Q.

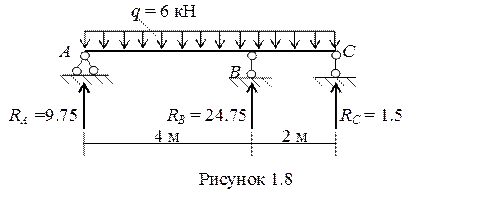
Sy = 0; R_A + R_B - q× 6 + R_С = 0; 9,75 + 24,75 - 6×6 + 1,5 = 36 – 36 = 0.

Sm_A = 0. R_B×4 - q×6×3 + R_С×6 = 24,75×4 - 6×6×3 + 1,5×6 = 108 – 108 = 0.

Проверка выполняется,

Пример 1.2. Построить эпюры внутренних усилий для заданной статически неопределимой плоской рамы, показанной на рисунке 1.9. Стойки и ригель рамы имеют одинаковую жесткость EI. При расчетах принять: l = 6 м, h = 4 м, М = 8 кНм и q = 4 кН/м.

Решение:

1 Проводим кинематический анализ заданной стержневой системы. Рама представляет собой один диск, соединенный с землей пятью связями: две в левой шарнирной опоре и три в правой жесткой опоре (в заделке). Независимых уравнений равновесия для плоского диска можно записать только три. Следовательно, рама дважды статически неопределима.

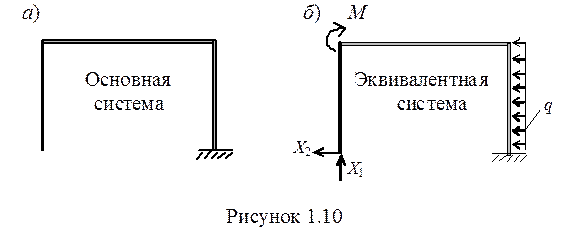
Воспользуемся для расчета данной рамы методом сил.

2 В соответствии с методом выбираем статически определимую основную систему путем отбрасывания лишних связей (рисунок 1.10, а). На рисунке 1.10, б показана эквивалентная система, полученная путем нагружения основной системы заданной нагрузкой и неизвестными усилиями Х₁ и Х₂, которые представляют собой реакции в отброшенных связях левой опоры.

3 Составляем канонические уравнения метода сил по числу лишних неизвестных

Х₁d₁₁ + Х₂d₁₂ + D_1р = 0

Х₁d₂₁ + Х₂d₂₂ + D_2р = 0.

4 При вычислении коэффициентов канонических уравнений, представляющих собой единичные перемещения, и свободных членов используем метод Мора в форме перемножения эпюр. Для этого построим единичные(рисунок 1.11, и рисунок 1.12) и грузовую (рисунок 1.13, б) эпюры моментов.

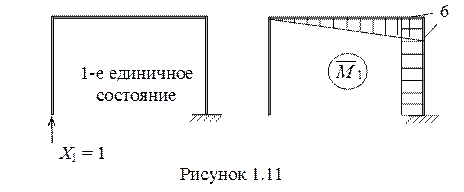
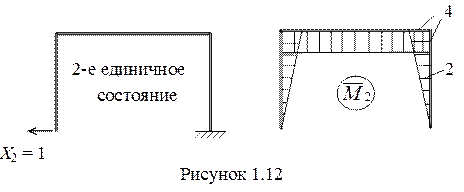
Для построения первой единичной эпюры создаем в основной системе первое единичное состояние, когда на раму действует усилие Х₁ = 1. Далее по участкам вычисляем моменты и строим эпюру, откладывая ординаты моментов со стороны растянутых волокон. Аналогичным образом поступаем при построении единичной эпюры .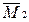

Грузовая эпюра, как правило, имеет более сложный вид. Рассмотрим подробнее построение грузовой эпюры – рисунок 1.13.

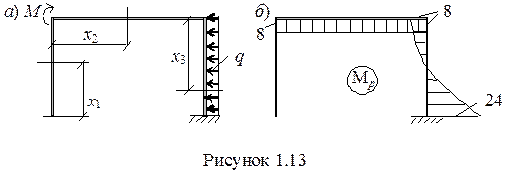
Создаем грузовое состояние (рисунок 1.13, а) и разбиваем раму на участки. При построении эпюр внутренних усилий в рамах используется следящая система координат, когда ось х, идущая вдоль оси стержня рамы, повторяет ее направление.

1-й участок: 0 < х₁ < 0.

Участок не нагружен, поэтому М₁ = 0

2-й участок: 0 < х₂ < 6.

М₂ = М, (правило знаков: в ригеле М > 0, если растягиваются нижние волокна, а в стойке М > 0, если растянуты левые волокна)

3-й участок: 0 < x₃ < 4м.

М₃= - М + qx₃²/2; M_х=0 = - 8 кН×м, M_x=2 = 0, М_х=4 = - 8 + 4×4²/2 = 24 кН×м

Выбираем масштаб по наибольшей ординате (24 кН×м) и строим грузовую эпюру М_р в соответствии с принятым правилом знаков - на растянутых волокнах (рисунок 1.13, б).

5 Вычисляем коэффициенты и свободные члены записанных канонических уравнений. Перемножение эпюр на каждом участке будем производить по правилу Верещагина с использованием для сложных эпюр формулы Симпсона.

Вычисляем единичные коэффициенты d_ij.

d₁₁ = 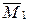× 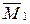= [(1/2) 6×6(2/3)6+6×4×6]/EI = 216EI;

d₂₂ = 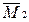× 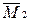= [(1/2) 4×4(2/3)4+4×6×4+(1/2)4×4(2/3)4]/EI = 416/3EI;

d₁₂ = d₂₁ = 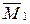× 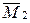= [(1/2)6×6×4+6×4×2]/EI = 120/EI.

Вычисляем свободные члены канонических уравнений, перемножая поочередно грузовую эпюру на единичные.

D_1p = M₀´ 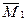= [8×6×3+(4/6)(6×8+4×6×0-6×24)]/EI = 80/EI;

D_2p = M₀´ 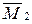= [8×6×4+(4/6)(8×4+4×2×0-24×0)]/EI = 640/3EI.

6 Проводим проверку коэффициентов канонических уравнений, которая осуществляется путем контроля выполнения равенств

Sd_ij = d_ss, (в)

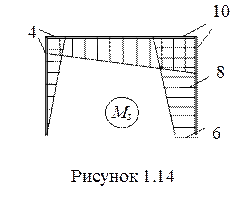
SD_ip = D_sp. (г)

Здесь: Sd_ij – сумма всех найденных единичных коэффициентов, d_ss, - результат перемножения суммарной единичной эпюры самой на себя, SD_ip – сумма грузовых коэффициентов (свободных членов), D_sp – результат перемножения грузовой эпюры на суммарную единичную эпюру.

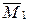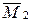Суммарную единичную эпюру М_s строим путем сложения единичных эпюр и (рисунок 1.149).

Вычисляем члены выражения (в).

Sd_ij =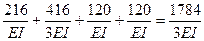

d_ss = М_s ´ М_s =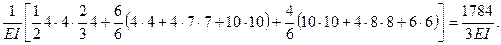

Условие (в) удовлетворяется. Вычисляем члены выражения (г).

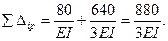
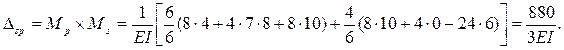
Условие (г) удовлетворяется. Проверки сошлись, коэффициенты вычислены верно. Канонические уравнения после подстановки коэффициентов и свободных членов имеют вид:

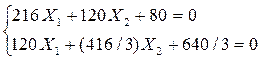
7 Решая полученную систему уравнений, получим следующие значения неизвестных:

Х₁ = 0,934 кН; Х₂ = -2,348 кН.

8 Строим результирующую эпюру моментов М, используя принцип суперпозиции:

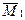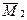М = М_Р + Х₁ + Х₂.

Для этого умножим единичные эпюры на соответствующие неизвестные Х₁ и Х₂, получив в результате эпюры М₁ и М₂ (рисунки 1.15, а, б), и сложим их по участкам с грузовой эпюрой М_Р.

В итоге получаем результирующую эпюру М (рисунок 1.15, в). Убедимся в правильности ее построения, проверив равновесие узлов рамы. Для этого вырежем в эпюре М левый и правый верхние узлы и покажем действующие в элементах, сходящихся в узле, изгибающие моменты с учетом растянутых волокон (рисунок 1.10, г). Мысленно записав уравнения моментов относительно центра каждого узла Sm=0, убеждаемся в равновесии узлов. Следовательно, сложение эпюр выполнено верно.

9 Для проверки самого решения проводим кинематическую проверку полученной эпюры моментов, перемножая результирующую эпюру на каждую единичную эпюру. Этим самым вычисляем перемещения по направлениям Х₁ и Х₂, которые должны быть равны нулю. Для примера покажем проверку по первому направлению.

М× 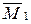= (6/6)(0×1,39+4×3×1,41+6×4,21) +

+ (4/6)(6×4,21+4×6×0,91-6×18,42) = 42,18 - 42,28 = -0,1

Погрешность вычисления d = (0,1×100%)/42,18 = 0,24%, что значительно меньше допустимой погрешности для ручного счета, равной 3%.

10 Для построения результирующей эпюры Q проведем графическое дифференцирование эпюры М по формуле:

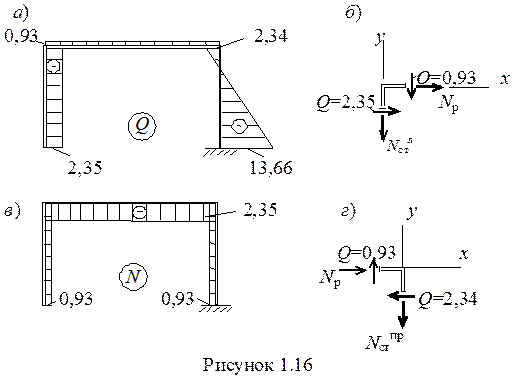
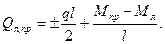(1.2)

При использовании выражения (2) необходимо расположить эпюру М на рассматриваемом участке длиной l горизонтально. При этом, в случае действия на участке равномерно распределенной нагрузки q, она должна действовать вниз. М_пр и М_л - значения моментов на участке справа и слева с учетом правила знаков для изгибающих моментов (момент, отложенный ниже оси эпюры, положителен, выше — отрицателен).

Так, для ригеля:

Q_р = [4,21 - (-1,36)]/6 = 0,93 кН

Для правой стойки:

Q_ст = ±(4×4)/2 + (-18,42 - 4,21)/4

Q_ст^л = 8 - 5,66 = 2.34 кН; Q_ст^пр = -8 -5,66 = -13,66 кН

Левая стойка:

Q_ст = (0 - 9,39)/4 = -2,35 кН

По полученным значениям Q выбираем масштаб и строим эпюру Q (рисунок 1.16, а).

11 Результирующую эпюру N строим используя эпюру Q, рассматривая равновесие узлов рамы под действием поперечных и продольных сил, действующих в стержнях, сходящихся в этих узлах. Вырежем левый верхний узел и покажем действующие в узле известные Q и неизвестные N (рисунок 1.16, б). Составим сумму проекций на ось х:

Sx = 0. Q_.ст^л + N_р = 0; N_p = -2,35 кН

Sу = 0. -Q_р - N_ст^л = 0; N_ст^л = - 0,93 кН

Знак «-» у продольной силы в ригеле N_p означает, что ригель сжат. Левая стойка тоже сжата. Вырезаем правый верхний узел (рисунок 1.16, г). Поскольку продольное усилие в ригеле известно, достаточно для определения продольной силы в правой стойке составить сумму проекций на ось у.

Sу = 0. Q_р- N_ст^пр =0; N_ст^пр = 0,93 кН.

Правая стойка растянута. Строим эпюру N (рисунок 1.16, в).

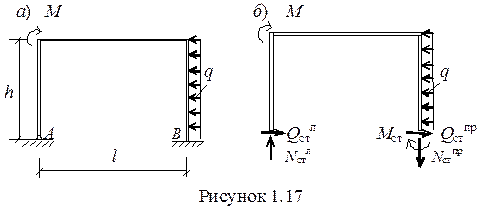
12 Проводим статическую поверку эпюр М, Q и N, которая заключается в проверке выполнения условий равновесия либо всей рамы под действием внешних активных и реактивных усилий, либо части рамы под действием внешних и внутренних усилий.

Проверим равновесие всей рамы (рисунок 1.17, а). Значений реакций берем из результирующих эпюр M,Q,N (рисунок 1.17, б).

Запишем для рамы уравнения проекций и уравнение моментов относительно правой опоры — точки В.

Sх = 0. -qh + Q_ст^л + Q_ст^пр = -16 + 2,34 + 13,66 = 16 – 16 = 0.

Sy = 0. N_ст^л - N_ст^пр = 0,93 – 0,93 = 0.

Sm_В = 0. -N_ст^л l - m - M_ст + qh²/2 = -32 + 32 = 0;

Все проверки выполняются. Таким образом, рассмотренная однопролетная одноэтажная статически неопределимая рама находится в равновесии.