Упрощения при расчете сложных рам

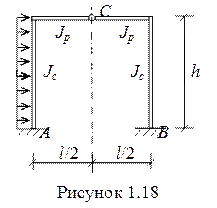
Симметричной называют такую раму, которая обладает симметрией в очертании оси, в расположении опорных устройств, в жесткости элементов.

Используя симметрию при выборе основной системы можно добиться значительного упрощения системы канонических уравнений за счет разделения ее на две независимые группы. Одна включает только симметричные неизвестные, другая - обратносимметричные неизвестные.

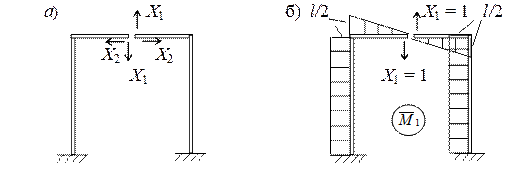
Так для рамы, показанной на рисунке 1.14 при выборе основной системы с учетом симметрии (рисунок 1.15,а) неизвестное Х₁ – обратносимметричное, а Х₂ – симметричное неизвестное. Построив соответствующие эпюры и вычислив коэффициенты канонических уравнений можно убедиться, что сложная система

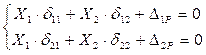
распалась на два простых уравнения, поскольку d₁₂ = d₂₁ = 0.

Х₁ d₁₁ = D_1p Х₂ d₂₂ = D_2p

1.4.2 Группировка неизвестных при расчете симметричных рам

В этом случае в качестве неизвестных следует принимать групповые неизвестные в виде системы сил, приложенных в различных, симметрично расположенных токах. В рассмотренном выше примере имели место групповые неизвестные, но они были вызваны тем, что представляли «освобожденные» внутренние усилия, выступавшие в качестве неизвестных, и должны быть приложены к обеим сторонам сечения.

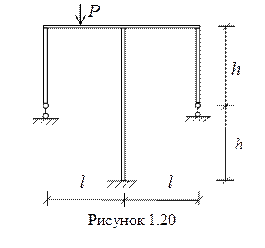
Рассмотрим в качестве примера дважды статически неопределимую систему, показанную на рисунке 1.20.

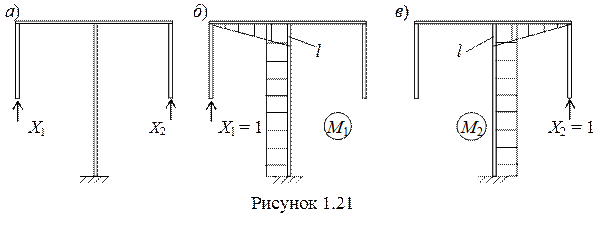
Произвольный выбор основной системы (рисунок 1.21,а) приводит к обычной системе канонических уравнений.

 

 

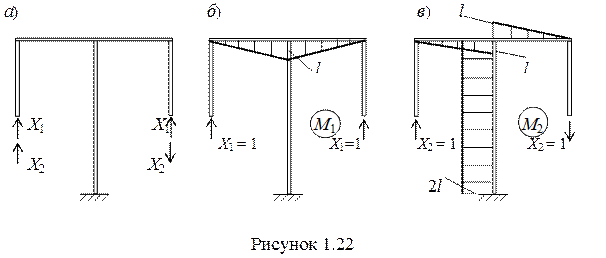
Если воспользоваться группировкой неизвестных (рисунок 1.22,а), то побочные коэффициенты d₁₂ = d₂₁ = 0 и система уравнений разделится на два простых уравнения.

Х₁ d₁₁ = D_1p,

Х₂ d₂₂ = D_2p.

 

 

Пример расчета симметричной рамы

Пример 1.3 Раскрыть статическую неопределимость и построить эпюры внутренних усилий для рамы, показанной на рисунке 1.19 ,а.

Решение.

1 Определяем степень статической неопределимости заданной стержневой системы. Она равна 3.

2 Выбираем основную систему с учетом симметрии рамы и воспользуемся групповыми неизвестными (рисунок 1.19, б).

3 Записываем систему канонических уравнений.

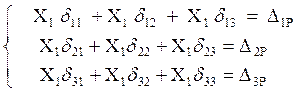
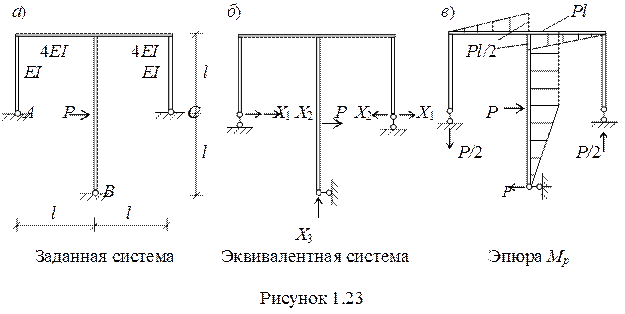
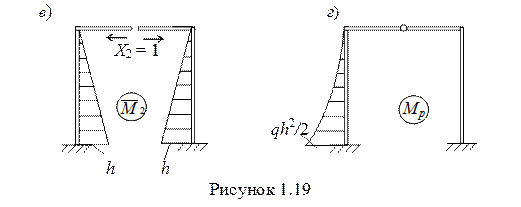
4 Для вычисления коэффициентов и свободных членной канонических уравнений строим грузовую (рисунок 1.23,в) и единичные (рисунок 1.24) эпюры.

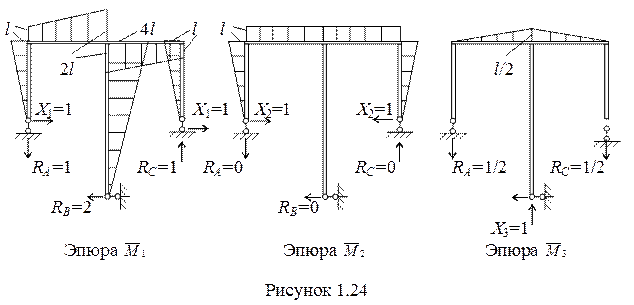
5 Проводим вычисление указанных коэффициентов.

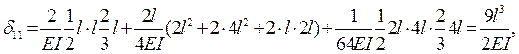
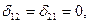
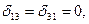(результат перемножения симметричной и кососимметричной эпюр).

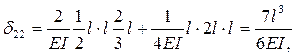
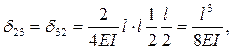
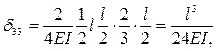
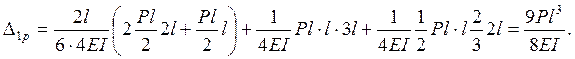
D_2p = D_3p = 0.

Система канонических уравнений принимает вид:

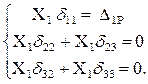
6 Решаем полученную систему алгебраических уравнений. Тогда:

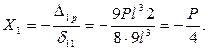
Система двух последних однородных уравнений с неизвестными Х₂ и Х₃ будет иметь ненулевое решение, если определитель из коэффициентов при неизвестных равен нулю.

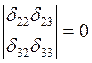
Вычислим определитель

d_{22 ∙}d₃₃ – 2∙d_{23 =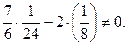} Следовательно Х₂ = Х₃ = 0.

7 Строим эпюру М₁ и результирующую эпюру М (рис. 1.25).

8 Выполняем кинематическую проверку – перемножение эпюр М и .

9 Дифференцируя эпюру М, получаем значения поперечных сил и строим эпюру Q (рисунок 1.26, а).

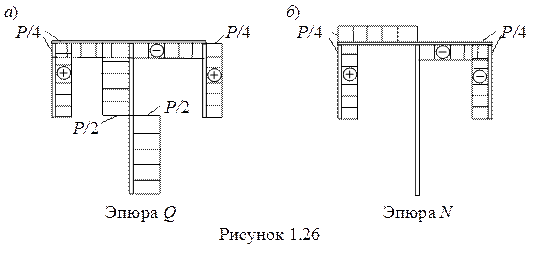
10 Рассматривая равновесие узлов эпюры Q, (рисунок 1.27), находим продольные усилия и строим эпюру N (рисунок 1.26, б).

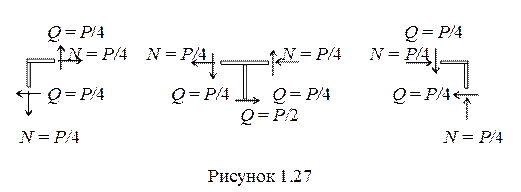
11 Выполняем статическую проверку рамы (рисунок 1.28).

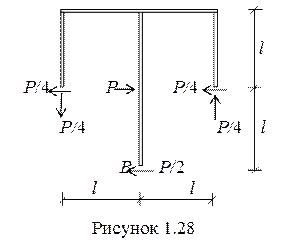
Sх = 0.

- Р/4+ Р – Р/4 – Р/2 = 0.

Sy = 0.

- Р/4+ Р/4 = 0.

Sm_В = 0.

Р/4∙l – Р∙l + Р/4∙l + Р/4∙l + Р/4∙l = 0.

Проверка выполняется.