Структурные схемы и уравнения САР

В системах автоматического регулирования типовые динамические звенья могут соединяться в различных сочетаниях. Поэтому, зная передаточные функции всех звеньев, возможно, составлять передаточную функцию САР или ее отдельных элементов и выходить на дифференциальное уравнение движения системы. Наиболее характерные объединения типовых звеньев можно заменить аналогом с соответствующей передаточной функцией, например, для случаев последовательного или параллельного соединения элементов, для звена, охваченного положительной или отрицательной обратной связью и т.п. При этом действия и получаемые выражения аналогичны анализу статики. Так, например, последовательное соединение n-звеньев может быть заменено одним звеном с передаточной функцией

.

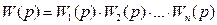Аналогично САР, состоящая из нескольких звеньев (см. рис. 5.27, б), заменяется одним звеном с передаточной функцией для замкнутой системы

; .

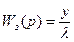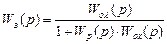При переходе к частотным передаточным функциям и соответственно к АФЧХ, ФЧХ и АЧХ необходимо принять 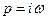при изменении частоты в пределах ,

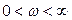где .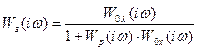

Таким образом, полученная передаточная функция САР после подстановки значений передаточных функций составляющих САР типовых элементов с предварительно определенными расчетом или экспериментом коэффициентами позволяет вычислить выражение .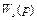

Далее, передаточная функция разворачивается в уравнение движения САР в операторной форме записи и затем может быть представлена в виде дифференциального уравнения. Решение дифференциального уравнения позволяет построить диаграмму переходного процесса САР при внесении того или иного возмущения с целью последующего анализа качества работы САР.

Синтез уравнения движения САР возможен другим путем. Сначала САР представляют в виде набора типовых звеньев (так называемый анализ САР). При составлении дифференциального уравнения звеньев выявляют физический закон, определяющий их поведение, например, закон сохранения энергии, равновесия сил.

Рассмотрим пример для простейшей САР уровня (рис. 5.27, а). Для этого составим структурную схему (рис. 5.527, б). Регулятор состоит из поплавка и рычага, т.е. представляет собой типовое идеальное звено (звено нулевого порядка) с передаточной функцией

.

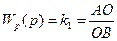Заслонку (регулирующий орган) и вентиль (нагрузка) объединяем с регулируемым объектом и описываем как типовое одноёмкостное звено с передаточной функцией

.

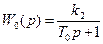Далее, составляем упрощенную структурную схему САРу (рис. 5.27, в) в виде звена, охваченного обратной отрицательной связью через регулятор уровня. И, наконец, определяем передаточную функцию САРу, используя выражение для простейшего аналога САРу (рис. 5.27, г)

.

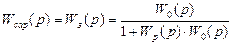Так как 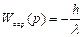(здесь знак определяется координатой 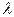), получим

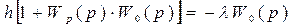
или

.

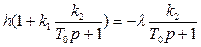После преобразования равенства получим

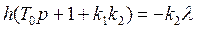
или

,

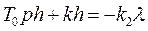где .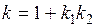

Разделив все члены уравнения на коэффициент 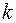и раскрыв оператор Лапласа 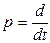, получим известное уравнение автоматики

,

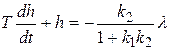где

.

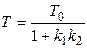Свойства и динамические характеристики этой САРу в полном объеме определяются графиками и выражениями.

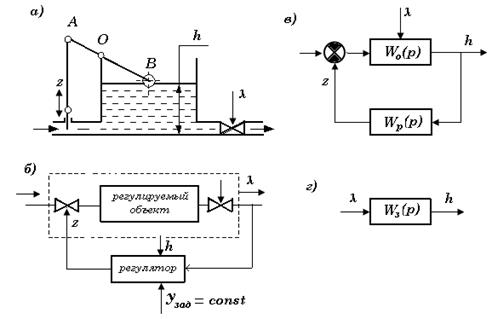
Рисунок 5.27. Функциональная и структурные схемы САРу

Уравнение статики САРу имеет вид

.

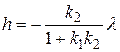По этому уравнению возможно построение статической характеристики системы автоматического регулирования уровня (она же является регуляторной характеристикой). Можно построить диаграмму переходного процесса САРу как .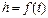

По передаточной функции САРу при подстановке в нее 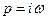при изменении частоты в пределах 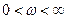возможно построить АФЧХ, АЧХ, ФЧХ и оценить качество функционирования системы автоматического регулирования уровня.

Данный подход в судовой автоматике является основным при исследовании и анализе сложных структур систем автоматического регулирования техническими средствами судна.

При использовании относительно несложных экспериментов определяются основные параметры, характеризующие уравнения движения элементов.

Далее проводится исследование передаточных функций и переходных процессов в системах автоматического регулирования с целью улучшения статических и динамических характеристик и показателей качества системы.