Устойчивость систем автоматического регулирования
Основная задача регулирования состоит в установлении и поддержании заданного режима работы объекта во времени. При этом качество процесса регулирования определяется рядом показателей, отраженных в государственных стандартах и требованиях нормативной документации, например, длительность переходного процесса, заброс регулируемого параметра, степень нечувствительности, степень неравномерности и т.п.
Если какое-либо возмущение нарушило равновесие в системе и далее исчезло, то при устойчивом регулировании после достаточно малого возмущения регулятор восстановит режим, который поддерживался до действия возмущения.
Для линейной САР устойчивость процесса регулирования по отношению к малым возмущениям означает его устойчивость также и по отношению к любому другому возмущению, не обязательно малому. Но сама линейная модель САР позволяет судить о поведении реальной системы лишь по отношению к малым возмущениям .
Рассмотрим дифференциальное уравнение движения САР (регулируемый параметр 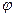 ) в операторной форме записи при возмущающем воздействии от изменения нагрузки λ
) в операторной форме записи при возмущающем воздействии от изменения нагрузки λ
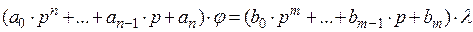 .
.
Данное уравнение является неоднородным дифференциальным уравнением. Его решение относительно 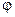 находится как сумма двух решений: частного решения с правой частью и общего решения уравнения без правой части. Таким образом, решение уравнения имеет вид:
находится как сумма двух решений: частного решения с правой частью и общего решения уравнения без правой части. Таким образом, решение уравнения имеет вид:
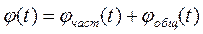
Первое слагаемое определяет вынужденную составляющую φв(t), второе слагаемое – переходную составляющую φn(t), 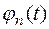 . Формула может быть представлена следующим образом:
. Формула может быть представлена следующим образом:
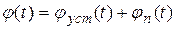 .
.
Характерный переходный процесс показан на рис. 5.28.
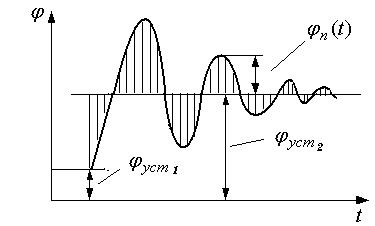
Рисунок 5.28. Характерный переходный процесс САР
САР является устойчивой, если при 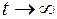 переходная составляющая стремится к нулю (
переходная составляющая стремится к нулю ( 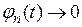 ). Найдем эту составляющую из уравнения.. Для этого решим уравнение без правой части
). Найдем эту составляющую из уравнения.. Для этого решим уравнение без правой части
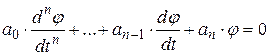 .
.
Определим корни характеристического уравнения
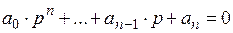 .
.
Так как данное уравнение содержит n корней, то переходную составляющую можем записать в виде
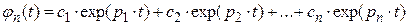 ,
,
где 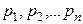 - корни характеристического уравнения;
- корни характеристического уравнения;
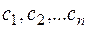 - постоянные интегрирования, определяемые из начальных условий.
- постоянные интегрирования, определяемые из начальных условий.
Корни характеристического уравнения определяются только левой частью уравнения, постоянные интегрирования - также и правой частью уравнения. Поэтому быстрота затухания и форма переходного процесса определяются как правой, так и левой частями исходного дифференциального уравнения.
Нахождение корней характеристического уравнения связано с трудностями. Однако находить их и не требуется, так как для суждения об устойчивости системы нужно лишь знать, что все они расположены левее мнимой оси на плоскости комплексного переменного р. Эти условия называются к р и т е р и я м и у с т о й ч и в о с т и.
Существующие критерии устойчивости делятся на две группы: алгебраические и частотные.
Алгебраические критерии устойчивости.
К р и т е р и й у с т о й ч и в о с т и Р а у з а - Г у р в и ц а.Задачу отыскания критерия устойчивости для систем, описываемых дифференциальными уравнениями любого порядка, сформулировал Максвелл в 1868г. Эта задача была впервые решена в алгебраической форме Раузом в 1873г. для уравнений четвертой и пятой степени. В 1877г. задача была решена полностью в виде алгоритма, определяющего последовательность математических операций, необходимых для решения.
Большее распространение получил алгебраический критерий устойчивости, сформулированный в 1895г. математиком Гурвицем.
Независимый подход Рауза и Гурвица к оценке устойчивости системы дал повод в мировой практике считать предложенный критерий – критерием Рауза-Гурвица.
Решение сводится к составлению матрицы коэффициентов уравнения (40), содержащую n строк и n столбцов.
Сначала заполняется главная диагональ матрицы коэффициентами от а1 до аn. Вверх (по вертикали) записываются последовательно коэффициенты с увеличивающимся индексом, вниз записываются коэффициенты с убывающими значениями индексов. Несуществующие коэффициенты (n<индекс<0) заменяются нулями.
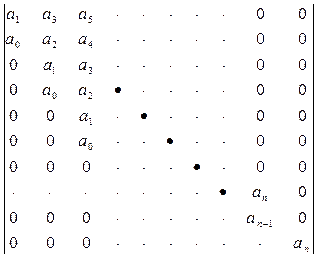
Оценка устойчивости сводится к тому, что при 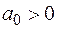 должны быть больше нуля все n определителей, получаемых из квадратной матрицы коэффициентов, определители (миноры) составляются по следующему правилу:
должны быть больше нуля все n определителей, получаемых из квадратной матрицы коэффициентов, определители (миноры) составляются по следующему правилу:
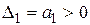 ;
; 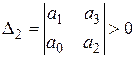 ;
; 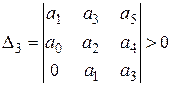 ; ……
; ……
Последний определитель включает в себя всю матрицу. Так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последний определитель выражается через предпоследний следующим образом:
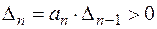 .
.
Однако в устойчивой системе предпоследний определитель должен быть положительным. Поэтому условие положительности последнего определителя сводится к условию 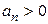 , т.е. к положительности свободного члена характеристического уравнения.
, т.е. к положительности свободного члена характеристического уравнения.
П р и м е р: САР имеет характеристическое уравнение
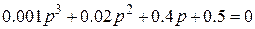 .
.
Оценить устойчивость САР по критерию Рауза - Гурвица.
Р е ш е н и е.
1. Составим квадратную матрицу, для чего сначала заполним главную диагональ коэффициентами, начиная с 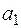 , а затем всю матрицу согласно правилу Рауза – Гурвица.
, а затем всю матрицу согласно правилу Рауза – Гурвица.
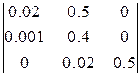
2. Определим значения миноров
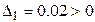 ;
; 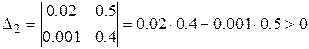 ;
;
 .
.
3. При положительном значении 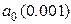 все миноры определителя больше нуля. Следовательно, система устойчива.
все миноры определителя больше нуля. Следовательно, система устойчива.
Частотные критерии устойчивости.
К р и т е р и й у с т о й ч и в о с т и М и х а й л о в а. Левая часть уравнения представляет собой характеристический полином или собственный оператор САР D(р)
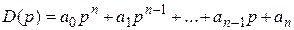 .
.
Если подставить в полином значение 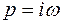 , где
, где 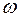 - круговая частота колебаний, соответствующих мнимому корню уравнения, то получим характеристический комплекс
- круговая частота колебаний, соответствующих мнимому корню уравнения, то получим характеристический комплекс
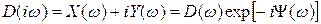 ,
,
где 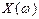 - вещественная часть, содержит четные степени
- вещественная часть, содержит четные степени
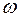 ,
, 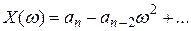 ;
;
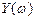 - мнимая часть, содержит нечетные степени
- мнимая часть, содержит нечетные степени 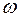 ,
,
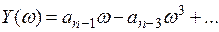 .
.
Функции 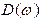 и
и 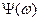 представляют собой модуль и фазу (аргумент) характеристического комплекса.
представляют собой модуль и фазу (аргумент) характеристического комплекса.
Уравнение не будет иметь корней в правой полуплоскости, если полное приращение аргумента 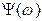 при изменении
при изменении 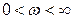 равно
равно 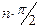 , где
, где 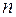 - степень полинома
- степень полинома 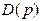 . САР будет при этом устойчивой. Если полное приращение окажется меньше
. САР будет при этом устойчивой. Если полное приращение окажется меньше 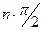 , то система неустойчива.
, то система неустойчива.
Чтобы установить связь между видом кривой Михайлова и знаками вещественных корней характеристического уравнения, определим, чему должен равняться угол поворота 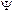 вектора
вектора 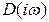 при
при 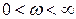 . Для этого запишем характеристический полином в виде произведения сомножителей
. Для этого запишем характеристический полином в виде произведения сомножителей
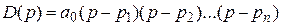 ,
,
где 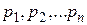 - корни характеристического уравнения.
- корни характеристического уравнения.
Характеристический вектор можно представить в виде
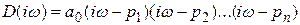 .
.
Каждое выражение в скобках представляет собой комплексное число. Следовательно, 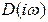 - произведение из комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора
- произведение из комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора 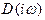 при изменении
при изменении 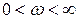 будет равен сумме углов поворота отдельных сомножителей
будет равен сумме углов поворота отдельных сомножителей
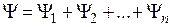 .
.
Если 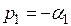 , где
, где 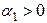 , то данный сомножитель будет
, то данный сомножитель будет 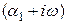 . При изменении
. При изменении 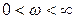 вещественная часть остается равной
вещественная часть остается равной 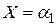 , а мнимая
, а мнимая 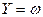 изменится от
изменится от
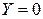 до
до 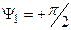 (рис. 5.29, а), т.е. на угол
(рис. 5.29, а), т.е. на угол 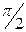 .
.
Если корень 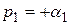 , где
, где 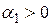 , то сомножитель
, то сомножитель 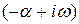 при изменении
при изменении 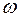 от
от 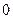 до
до 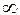 изменится таким образом, что вектор повернется на угол от
изменится таким образом, что вектор повернется на угол от 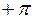 до
до 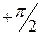 , т.е. на угол
, т.е. на угол 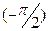 (рис. 5.29, б).
(рис. 5.29, б).
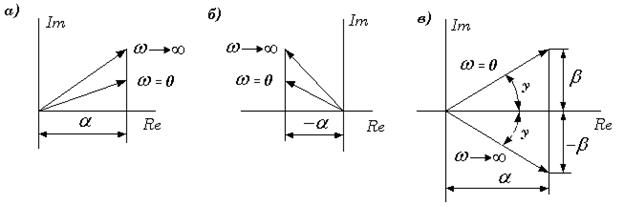
Рисунок 5.29. Анализ сомножителей характеристического вектора
Если корни равны 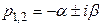 , то сомножители
, то сомножители 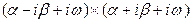 при аналогичном изменении
при аналогичном изменении 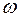 повернутся на углы
повернутся на углы 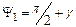 и
и 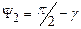 (см. рис. 5.29, в). Тогда вектор, соответствующий данному произведению повернется на угол
(см. рис. 5.29, в). Тогда вектор, соответствующий данному произведению повернется на угол 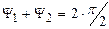 .
.
Аналогично, если 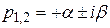 , то
, то 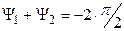 .
.
Таким образом, если характеристическое уравнение из 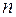 корней будет иметь
корней будет иметь 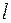 корней с положительной вещественной частью, то каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворота, равная
корней с положительной вещественной частью, то каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворота, равная 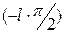 , всем же остальным
, всем же остальным 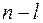 корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворота, равная
корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворота, равная 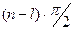 . Общий угол поворота вектора
. Общий угол поворота вектора 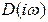 при изменении
при изменении 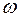 от
от 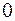 до
до 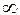
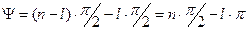 .
.
В общем случае i-й сомножитель 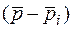 выражения в векторной форме можно представить в комплексной плоскости (рис. 5.30) при подстановке
выражения в векторной форме можно представить в комплексной плоскости (рис. 5.30) при подстановке 
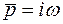 .
.
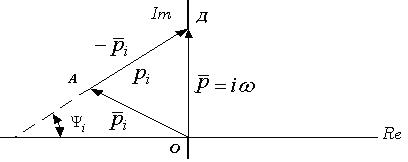
Рисунок 5.30. Представление i-го сомножителя характеристического вектора 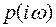
Каждый сомножитель 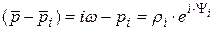 ,
,
где 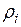 - модуль вектора
- модуль вектора 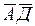 ;
;
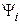 - фазовый угол вектора
- фазовый угол вектора 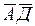 (его аргумент).
(его аргумент).
Тогда уравнение можно представить как
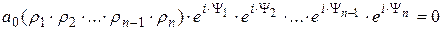
или 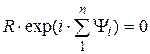 ,
,
где R - модуль Михайлова, 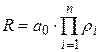 .
.
Если изменять частоту 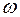 от
от 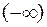 до
до 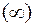 , то угол
, то угол 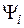 каждого из векторов изменится от
каждого из векторов изменится от 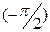 до
до 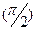 .
.
К р и т е р и й М и х а й л о в а читается так:
для устойчивости системы необходимо и достаточно, чтобы годограф вектора 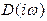 в комплексной плоскости, полученный в результате подстановки
в комплексной плоскости, полученный в результате подстановки 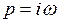 в характеристическое уравнение, при изменении
в характеристическое уравнение, при изменении 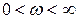 , нигде не обращаясь в н у л ь, развернулся п о с л е д о в а т е л ь н о против часовой стрелки на угол
, нигде не обращаясь в н у л ь, развернулся п о с л е д о в а т е л ь н о против часовой стрелки на угол 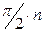 (где
(где 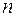 - степень уравнения).
- степень уравнения).
Пример: CАР описана дифференциальным уравнением
движения
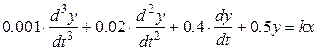 .
.
Оценить устойчивость САР по критерию Михайлова.
Решение:
Запишем уравнение в операторной форме:
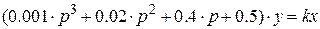 .
.
Приравняв собственный оператор нулю 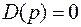 , по-
, по-
лучим характеристическое уравнение
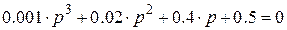 .
.
Делаем подстановку 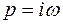
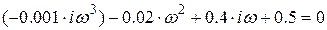
и выделяем вещественную и мнимую части ( 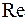 и
и 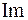 ):
):
Вещественная часть 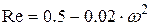 ;
;
Мнимая часть 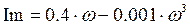 .
.
Для отыскания точек годографа составим табл. 5.1.
Таблица 5.1
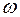
| |||||||
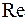
| 0.5 | 0.48 | -1.5 | -7.5 | -49 | -199 | |
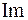
| 0.4 | 1.9 | -105 | -960 |
Строим годограф вектора на комплексной плоскости (рис.5.31).При 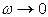
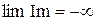 , т.е. годограф вектора последовательно и не обращаясь в нуль повернется против часовой стрелки на угол, не превышающий значения
, т.е. годограф вектора последовательно и не обращаясь в нуль повернется против часовой стрелки на угол, не превышающий значения 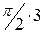 . Таким образом, САР устойчива.
. Таким образом, САР устойчива.
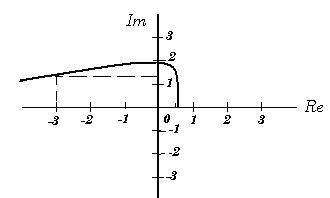
Рисунок 5.31. Годограф Михайлова
К р и т е р и й у с т о й ч и в о с т и Н а й к в и с т а основан на построении амплитудно-фазово-частотной характеристики р а з о м к н у т о й системы при изменении частоты 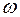 от
от 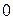 до
до 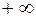 .
.
Устойчивость системы определяется в следующем порядке:
· Строится структурная схема САР;
· Разрывают замкнутую систему, нарушая одну из связей контура (рис. 5.32,а);
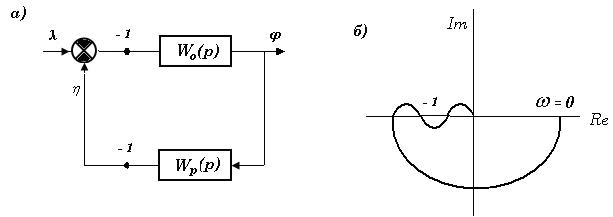
Рисунок 5.32. Структурная схема САР и ее АФЧХ
· Определяют передаточную функцию разомкнутой системы
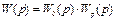 ;
;
· Строят АФЧХ разомкнутой системы
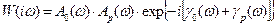 ,
,
где 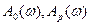 - соответственно амплитудно-частотные характеристики объекта и регулятора;
- соответственно амплитудно-частотные характеристики объекта и регулятора;
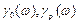 - соответственно фазово-частотные характеристики объекта и регулятора.
- соответственно фазово-частотные характеристики объекта и регулятора.
Введя замену 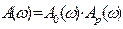 для разомкнутой системы, получим АФЧХ
для разомкнутой системы, получим АФЧХ
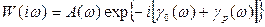 ;
;
Для устойчивости САР необходимо и достаточно, чтобы АФЧХ соответствующей разомкнутой системы не охватывала на комплексной плоскости точку с координатами (-1, 10). Произвольная АФЧХ устойчивой системы показана на рис. 5.32, б.
П р и м е р: Оценить устойчивость САРч с регулятором прямого действия с помощью критерия Найквиста, если степень неравномерности регулятора 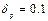 , время двигателя
, время двигателя 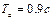 , время регулятора
, время регулятора 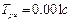 , время катаракта
, время катаракта 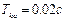 , степень неравномерности статической характеристики двигателя
, степень неравномерности статической характеристики двигателя 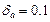 .
.
Решение:
Определим передаточную функцию разомкнутой системы
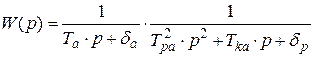 .
.
Определим АФЧХ значение 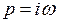 и получим выражение для АФЧХ разомкнутой системы, где
и получим выражение для АФЧХ разомкнутой системы, где 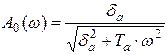 ;
;
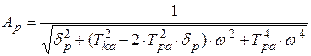 .
.
Определим АЧХ 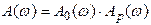 при изменении
при изменении 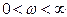 , результаты сведем в табл. 5.2.
, результаты сведем в табл. 5.2.
Определим ФЧХ, где 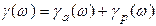
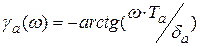
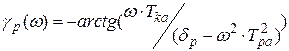
Результаты расчета 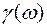 при
при 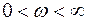 сведем в табл. 5.2.
сведем в табл. 5.2.
Таблица 5.2
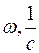
| 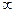
| ||||||||
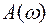
| 9,28 | 7,81 | 6,4 | 5,3 | 4,47 | 2,42 | 1,64 | ||
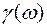
| -21,7 | -38,5 | -49 | -57,7 | -61,3 | -75,6 | -80,2 |
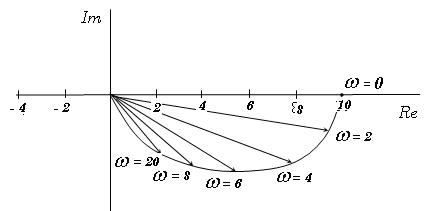
Рисунок 5.33. Амплитудно-фазовая частотная характеристика
Дата добавления: 2019-09-30; просмотров: 836;











