Статическая характеристика системы автоматического регулирования
Составим уравнение статики для всех элементов наиболее распространенной линейной САР (рис. 5.17, а).
САР, статика элементов, которой описывается уравнением вида 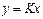 , называется линейной.
, называется линейной.
Составим систему уравнений, описывающих статику всех звеньев линейной САР.
|
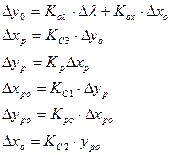
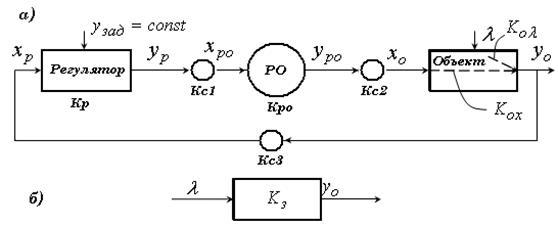
Рисунок 5.17. Структурная схема типовой линейной САР:
а – развернутая схема; б – упрощенная схема
Подставив в первое уравнение 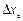 из последнего, и далее вместо
из последнего, и далее вместо 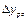 его значение из предпоследнего и т.д., получим выражение
его значение из предпоследнего и т.д., получим выражение
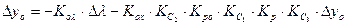 ,
,
или
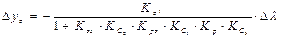
.
САР является замкнутой системой, составленной из конечного числа звеньев, при этом главная обратная связь проходит от выходной координаты объекта через регулятор на входную координату и является отрицательной. Обозначим через К произведение коэффициентов статической передачи последовательно расположенных элементов (как бы для разомкнутой цепочки звеньев):
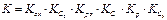 ,
,
где 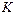 – коэффициент статической передачи разомкнутой САР.
– коэффициент статической передачи разомкнутой САР.
Тогда вместо системы уравнений получим выражение
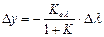
или 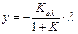 .
.
Введя коэффициент Кз для замкнутой системы элементов Кз = Коλ : (1+К), получим вместо системы уравнений уравнение статики САР
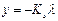
а структурная схема САР упростится (см. рис. 5.17, б).
Полученное выражение справедливо для САР с любым количеством звеньев. При астатическом регуляторе 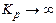 и тогда
и тогда 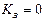 , т.е. тогда отсутствует зависимость выходной координаты О от нагрузки,
, т.е. тогда отсутствует зависимость выходной координаты О от нагрузки, 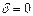 (точное регулирование). Если через регулятор будет проходить положительная обратная связь, то
(точное регулирование). Если через регулятор будет проходить положительная обратная связь, то 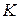 будет противоположного знака и
будет противоположного знака и
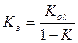 .
.
Дата добавления: 2019-09-30; просмотров: 823;











